Розподіл молекул газу за швидкостями. Закон Максвелла
ФІЗИКА
Частина 2 МОЛЕКУЛЯРНА ФІЗИКА І ТЕРМОДИНАМІКА
Розділ 4 ОСНОВИ МОЛЕКУЛЯРНО-КІНЕТИЧНОЇ ТЕОРІЇ ГАЗІВ
4.7. Розподіл молекул газу за швидкостями. Закон Максвелла
У рівноважному стані параметри газу залишаються незмінними, проте мікростани – взаємне розташування молекул, їхні швидкості – безперервно змінюються.
Оскільки всі напрями руху рівноймовірні, розподіл молекул за напрямом буде рівномірним. Швидкості молекул становлять від нуля до нескінченності. Ці значення не є рівно ймовірними.
Дуже великі й дуже малі
Отже, розподіл молекул за швидкостями не довільний і має підлягати певному закону. Цей закон стосується не кожної даної молекули, а всієї сукупності молекул, тобто він є статистичним. Закон розподілу молекул за швидкостями встановив Дж. Максвелл у 1869 р. Обгрунтуванню та встановленню меж застосування його присвячені наукові праці російського фізика М.
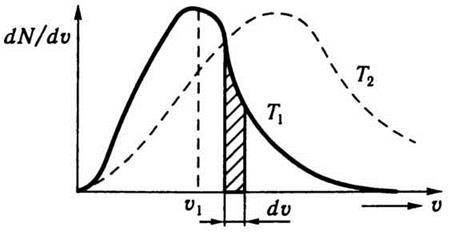
Рис. 4.2
По осі абсцис відкладено значення швидкості окремих молекул газу. Якщо υ і υ + dυ – досить близькі значення швидкості, а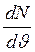 
– відповідне середнє значення ординати, то 
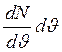=dN (площа елементарної смуги під кривою) є числом молекул, швидкість яких лежить у межах від υ до υ + dυ. Тоді площа під кривою дорівнюватиме загальному числу молекул досліджуваного газу N. Вважають також, що всі молекули цього газу однакові й температура в усіх частинах газу та сама.
Розглядаючи криві розподілу швидкостей молекул, можна зазначити такі особливості їх:
1. Крива розподілу швидкостей молекул газу проходить через початок координат. Отже, немає молекул, які б не рухались.
2. Крива має максимум, після якого асимптотично наближається до осі абсцис. Отже, дуже великі швидкості малоймовірні. Це можливо тільки за умови, що молекула при багатьох зіткненнях з іншими молекулами діставатиме енергію, а не віддаватиме її, що є неймовірним.
3. Крива розподілу швидкостей несиметрична – з одного боку спад кривої крутіший, ніж з другого.
Закон розподілу Максвелла можна записати так:
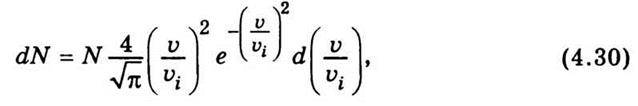
Де N – загальне число молекул у заданій масі газу; dN – число молекул, швидкості яких лежать у межах від υ до υ + dυ; υі – найімовірніша швидкість.
На рис. 4.2 крива, зображена штриховою лінією, відповідає розподілу молекул за швидкостями при більш високій температурі, ніж температура, якій відповідає крива, зображена суцільною лінією. Зіставлення цих двох кривих наочно виявляє особливості розподілу Максвелла. Крива Максвелла з підвищенням температури стає більш пологою: це означає, що розподіл молекул за швидкостями стає рівномірнішим. Чим вища температура, тим вище піднімається права частина кривої і тим нижче опускається її ліва частина. Це означає, що з підвищенням температури збільшується частина молекул, швидкості яких перевищують найімовірнішу швидкість, і зменшується частина молекул з малими швидкостями.
Швидкість υi, яка відповідає максимуму кривої розподілу швидкостей молекул (див. рис. 4.2), називається найімовірнішою швидкістю. Згідно з теорією Максвелла найімовірнішу швидкість можна визначити за формулою
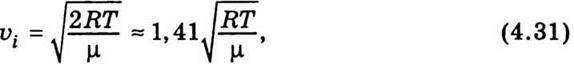
Де R – універсальна газова стала; Т – абсолютна температура; μ – молярна маса.
Середня квадратична швидкість визначається так:
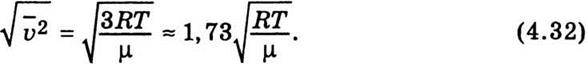
Середню арифметичну швидкість, згідно з теорією, можна обчислити за формулою
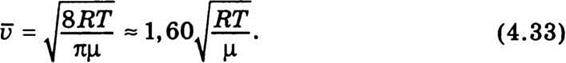
Виходячи зі співвідношень (4.31)-(4.33), можемо записати таку нерівність:
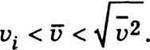
Будь-якому явищу, що відбувається в середовищі з великою кількістю частинок, властивий статистичний характер. Такі явища підлягають законам великих чисел. Закон розподілу молекул за швидкостями є типовим прикладом статистичного закону. Висновки з нього мають імовірнісний характер.
Слід зазначити, що встановлений Максвеллом закон розподілу молекул за швидкостями і всі висновки з нього справджуються лише для газу, що перебуває у рівноважному стані.
(1 votes, average: 5.00 out of 5)
Loading...