Розв’язання трикутників
Геометрія
Розв’язування трикутників
Розв’язування трикутників
Розв’язування трикутників полягає у знаходженні невідомих сторін і кутів трикутника за відомими його сторонами та кутами.
Результати в таких задачах наближені, тому що для більшості значень кутів наближеними є значення їх синуса і косинуса.
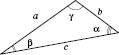
Задача 1. Розв’язати трикутник за стороною й двома прилеглими кутами.
На рисунку в трикутнику дано: a; 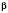 ;
; 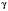 .
.
Знайти:  ; b; c.
; b; c.
Розв’язання
1)
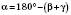 (за теоремою про суму кутів трикутника).
(за теоремою про суму кутів трикутника).2) За теоремою синусів:
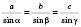 .
.Отже,
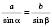 ,
, 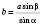 ,
,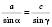 ,
, 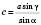 .
.Задача має розв’язання завжди, коли
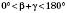 , причому цей розв’язок буде єдиним.
, причому цей розв’язок буде єдиним.Задача 2. Розв’язати трикутник за двома сторонами й кутом між ними.
Дано: a; b;
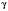 .
.Знайти: c;
 ;
; 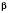 .
.Розв’язання
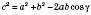 ;
;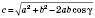 .
.2) За теоремою косинусів:
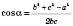 .
.За таблицями або за допомогою калькулятора знаходимо наближене значення
 .
.3) За теоремою про суму кутів трикутника:
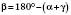 .
.Задача завжди має розв’язання, причому розв’язок буде єдиним.
Зверніть увагу: при розв’язанні задачі 2 для знаходження невідомих кутів можна користуватися теоремою синусів. Але тоді доцільно починати з того невідомого кута, який буде меншим, тобто лежить проти меншої сторони. Цей кут обов’язково буде гострим, тобто за значенням його синуса можна буде визначити єдине значення кута.
Задача 3. Розв’язати трикутник за двома сторонами й кутом, протилежним одній із цих сторін.
Дано: a; b;
 .
.Знайти: c;
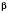 ;
; 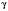 .
.Розв’язання
1) За теоремою синусів:
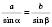 ;
; 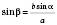 .
.За таблицями або за допомогою калькулятора знаходимо наближене значення
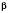 .
.Зверніть увагу: на цьому етапі можна одержати
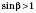 . Тоді задача не має розв’язків. Якщо за умовою
. Тоді задача не має розв’язків. Якщо за умовою 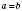 ,
, 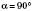 або
або 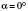 , або
, або 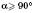 , задача теж не має розв’язку.
, задача теж не має розв’язку.Якщо ми отримаємо
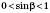 , задача матиме два розв’язки, тому що одне й те саме значення
, задача матиме два розв’язки, тому що одне й те саме значення 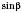 буде у двох кутів – тупого й гострого, які в сумі дають
буде у двох кутів – тупого й гострого, які в сумі дають 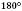 . (За тотожністю
. (За тотожністю 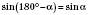 .) Подальше розв’язання тоді проводять окремо для кожного значення
.) Подальше розв’язання тоді проводять окремо для кожного значення 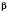 .
.2) За теоремою про суму кутів трикутника:
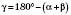 .
.3) За теоремою синусів:
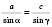 ;
; 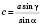 .
.Задача 4. Розв’язати трикутник за трьома сторонами.
Дано: a; b; c. Знайти:
 ,
, 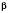 ,
, 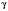 .
.Розв’язання
1) За теоремою косинусів:
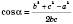 ;
; 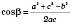 .
.Знаходимо наближені значення
 і
і 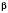 .
.2) За теоремою про суму кутів трикутника:
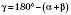 .
.Задача не матиме розв’язків, якщо найбільша з даних сторін не менша за суми двох інших. В інших випадках задача має один розв’язок.