Головна ⇒ 📌Довідник з математики ⇒ Розв’язування рівнянь графічним способом
Розв’язування рівнянь графічним способом
Математика – Алгебра
Функції
Розв’язування рівнянь графічним способом
За допомогою графіків функцій можна розв’язувати рівняння графічним способом. Для цього треба побудувати в одній системі координат графіки обох частин рівняння й знайти абсциси точок їх перетину.
Приклад. Розв’яжіть рівняння 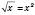 .
.
Побудуємо графіки функції 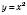 і
і 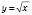 в одній координатної системі (див. рисунок) і знайдемо абсиси точок їх перетину.
в одній координатної системі (див. рисунок) і знайдемо абсиси точок їх перетину.
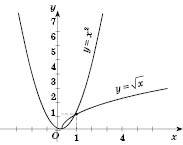
Відповідь: 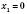 ,
, 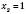 .
.
Related posts:
- Системи лінійних рівнянь з двома невідомими – Системи лінійних рівнянь Математика – Алгебра Системи лінійних рівнянь Системи лінійних рівнянь з двома невідомими Якщо треба знайти спільні розв’язки кількох рівнянь, то кажуть, що ці рівняння утворюють Систему рівнянь. Розв’язок системи рівнянь з двома невідомими – пара значень невідомих, яка є розв’язком кожного з рівнянь системи. Розв’язати систему рівнянь означає знайти всі її розв’язки або довести, що […]...
- Розв’язування систем двох лінійних рівнянь з двома змінними способом підстановки Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ & 28. Розв’язування систем двох лінійних рівнянь з двома змінними способом підстановки Графічний спосіб розв’язування систем рівнянь є досить громіздким і до того ж не завжди допомагає знайти точні розв’язки. Розглянемо інші (не графічні) способи розв’язування систем лінійних рівнянь з двома змінними, які називають аналітичними. Почнемо зі способу […]...
- Розв’язування систем рівнянь Математика – Алгебра Розв’язування систем рівнянь Розглянемо системи рівнянь, в яких одне або обидва рівняння другого степеня. 1. Щоб розв’язати систему рівнянь графічним способом, треба побудувати в одній системі координат графіки обох рівнянь системи й знайти координати точок перетину графіків. Ці точки і будуть розв’язками системи рівнянь. Наприклад: Графіком першого рівняння є коло з центром […]...
- Розв’язання систем лінійних рівнянь способом підстановки Рівень А Відповідь: (1; 3). Відповідь: (7; -4,5). Відповідь: (1; 3). Відповідь: (4; 1). Відповідь: (3; 1). Відповідь: (1;-2). Відповідь: розв’язків немає. Відповідь: (3; 2). Відповідь: (4; 0). Відповідь: (3; 5). Відповідь: (1,5; 2). Відповідь: (3; -1). Відповідь: (7; 1). Відповідь: (1; -1). Рівень Б Відповідь: (2; 1,5). Відповідь: (1; -2). Відповідь: (20; 0,5). Відповідь: […]...
- Системи двох лінійних рівнянь із двома змінними А) х = 2; у = 1 – розв’язок системи, бо 2 – 2 • 1 = 0 – правильна рівність; 2 + 3 • 1 = 5 – правильна рівність; Б) x = 0; у = 0 – не є розв’язком системи, бо 0 – 2 • 0 = 0 – правильна рівність, а […]...
- Розв’язування показникових рівнянь УРОК 46 Тема. Розв’язування показникових рівнянь Мета уроку. Формування умінь учнів розв’язувати показникові рівняння способом зведення до спільної основи; способом винесення за дужки спільного множника; способом зведення до спільного показника; графічним способом. І. Перевірка домашнього завдання Два учні на відкидних дошках відтворюють розв’язування вправ відповідно № 1, 3, 5, 7, 9 і № 2, 4, […]...
- Розв’язування систем двох лінійних рівнянь з двома змінними способом додавання Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ & 29. Розв’язування систем двох лінійних рівнянь з двома змінними способом додавання Тепер розглянемо ще один аналітичний спосіб розв’язування систем двох лінійних рівнянь з двома змінними – спосіб додавання. Розв’язуючи систему способом додавання, ми переходимо від даної системи до рівносильної їй системи, одне з рівнянь якої містить лише […]...
- Розв’язування тригонометричних рівнянь способом зведення до однієї тригонометричної функції УРОК 23 Тема. Розв’язування тригонометричних рівнянь способом зведення до однієї тригонометричної функції Мета уроку: формування умінь учнів розв’язувати тригонометричні рівняння способом зведення до однієї тригонометричної функції (алгебраїчний спосіб). І. Перевірка домашнього завдання 1. Відповіді на питання, що виникли у учнів при виконанні домашніх завдань. 2. Самостійна робота. Розв’яжіть рівняння: A) cosx = . (3 бали) […]...
- Система двох лінійних рівнянь з двома змінними та її розв’язок. Розв’язування систем лінійних рівнянь з двома змінними графічно Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ & 27. Система двох лінійних рівнянь з двома змінними та її розв’язок. Розв’язування систем лінійних рівнянь з двома змінними графічно Приклад 1. Маска й трубка для підводного плавання разом коштують 96 грн, причому маска на 16 грн дорожча за трубку. Скільки коштує маска і скільки трубка? Р о […]...
- Завдання для перевірки знань до §§ 19-21 1. 1) у = х2 + х; 3) – функції. 2. 1) у = 3х – 7; 3) у = 4 – лінійні функції. 3. 1) у = -2х + 6; k = -2; l = 6; 2) у = 7,4x; k = 7,4; l = 0. 4. у = -2х + 7; 1) х […]...
- Розв’язування систем лінійних рівнянь із двома змінними способом додавання Урок № 76 Тема. Розв’язування систем лінійних рівнянь із двома змінним способом додавання Мета: сформувати в учнів усвідомлення необхідності знання алгоритму розв’язування лінійних рівнянь способом додавання та розуміння кожного кроку в цьому алгоритмі; виробити вміння використовувати названий алгоритм під час розв’язування систем лінійних рівнянь. Тип уроку: засвоєння вмінь та навичок. Хід уроку I. Організаційний момент […]...
- Графік лінійного рівняння з двома невідомими – Системи лінійних рівнянь Математика – Алгебра Системи лінійних рівнянь Графік лінійного рівняння з двома невідомими Графіком рівняння з двома невідомими називається множина всіх точок координатної площини, координати котрих є розв’язками цього рівняння. Графіком рівняння , у якому хоча б один із коефіцієнтів (a або b) відмінний від нуля, є пряма. Для побудови будь-якої прямої досить знати координати двох […]...
- Розв’язування тригонометричних рівнянь способом розкладання на множники УРОК 24 Тема. Розв’язування тригонометричних рівнянь способом розкладання на множники Мета уроку: фрмування умінь учнів розв’язувати тригонометричні рівняння способом розкладання на множники. І. Перевірка домашнього завдання Перший учень пояснює розв’язування вправи № 2 (23), другий учень – вправи № 2 (30), третій – вправи № 2 (37). II. Сприймання і усвідомлення нового матеріалу Багато тригонометричних […]...
- Розв’язування систем лінійних рівнянь із двома змінними способом підстановки Урок № 75 Тема. Розв’язування систем лінійних рівнянь із двома змінними способом підстановки Мета: закріпити знання алгоритму розв’язування систем лінійних, рівнянь із двома змінними способом підстановки; вдосконалити вміння і навички, необхідні для застосування названого алгоритму; повторити матеріал попередньої теми щодо кількості розв’язків системи лінійних рівнянь залежно від співвідношення відповідних коефіцієнтів рівнянь. Тип уроку: засвоєння вмінь […]...
- Розв’язання систем лінійних рівнянь способом додавання Рівень А Відповідь: (4; 3). Відповідь: (-2; -3). Відповідь: (0,5; 1). Відповідь: (-1;2). Відповідь: (-2; 4). Відповідь: (5; 1). Відповідь: (3; -1). Відповідь: (0; -2). Відповідь: (-1; 3). Відповідь: (-1; -1). Відповідь: (2; -2). Відповідь: (4; -3). Відповідь: (-0,5; 0,5). Відповідь: (1; -1). Відповідь: (1; -2). Відповідь: (1; -2). Відповідь: (5; 6). Відповідь: (5; 0,5). […]...
- СИСТЕМА ДВОХ ЛІНІЙНИХ РІВНЯНЬ ІЗ ДВОМА ЗМІННИМИ РОЗДІЛ 5 ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ &23. СИСТЕМА ДВОХ ЛІНІЙНИХ РІВНЯНЬ ІЗ ДВОМА ЗМІННИМИ Ви вже знаєте, як розв’язати задачу за допомогою лінійного рівняння з однією змінною. За допомогою лінійних рівнянь із двома змінними також можна розв’язувати задачі. Розглянемо приклад. Задача 1. Сума двох чисел дорівнює 3, а різниця подвоєного першого числа і потроєного […]...
- Системи рівнянь з двома змінними. Графічний спосіб розв’язування систем рівнянь з двома змінними УРОК № 30 Тема. Системи рівнянь з двома змінними. Графічний спосіб розв’язування систем рівнянь з двома змінними Мета уроку: закріпити знання учнів про зміст означень: графік рівняння з двома змінними, система рівнянь з двома змінними, розв’язок системи рівнянь з двома змінними, а також алгоритмів побудови графіка рівняння з двома змінними та графічного способу розв’язування системи […]...
- Система двох лінійних рівнянь із двома змінними та її розв’язок Урок № 72 Тема. Система двох лінійних рівнянь із двома змінними та її розв’язок Мета: сформувати уявлення учнів про розв’язок системи рівнянь із двома змінними та графічний спосіб розв’язання систем лінійних рівнянь; виробити вміння: здійснювати перевірку, чи є пара (х; у) розв’язком даної системи лінійних рівнянь; використовуючи навички побудови графіка лінійного рівняння з двома змінними, […]...
- Система двох лінійних рівнянь із двома змінними (1; 5) не є розв’язком системи, бо не задовольняє другому рівнянню; (2; 4) не є розв’язком системи, бо не задовольняє другому рівнянню. 1102. 1) мал. 80; (2; 1); 2) мал. 81: (2; 3); 3) мал. 82: (3; 3). 1103. 1) 1; 3; 5; 2) -3; 1; 4; 3) -3; 1; -5. 2 розв’язки до першого […]...
- Приклади функцій і їх графіків Математика – Алгебра Функції Приклади функцій і їх графіків Лінійна функція Лінійною називається функція, яку можна задати формулою , де х – аргумент, а k і b – дані числа. Графік лінійної функції – пряма. k називається Кутовим коефіцієнтом прямої, яка є графіком лінійної функції. Кожна пряма на координатній площині, яка не є перпендикулярною до […]...
- Розв’язування систем лінійних рівнянь з двома змінними способом додавання Урок № 77 Тема. Розв’язування систем лінійних рівнянь з двома змінними способом додавання Мета: закріпити знання алгоритму розв’язання систем лінійних рівнянь із двома змінними способом додавання; відпрацювати вміння і навички, використання яких передбачено алгоритмом; ознайомити учнів із нестандартними задачами на застосування систем. Тип уроку: засвоєння вмінь та навичок. Хід уроку I. Організаційний момент 1. Перевірка […]...
- СИСТЕМА ДВОХ ЛІНІЙНИХ РІВНЯНЬ З ДВОМА ЗМІННИМИ. ГРАФІЧНИЙ СПОСІБ РОЗВ’ЯЗАННЯ СИСТЕМ Цілі: – навчальна: сформувати поняття системи двох лінійних рівнянь з двома змінними, розв’язку системи двох лінійних рівнянь з двома змінними; сформувати вміння розв’язувати системи рівнянь графічним способом; – розвивальна: формувати вміння аналізувати інформацію; розвивати увагу, логічне мислення, пам’ять; – виховна: виховувати наполегливість у досягненні мети, зацікавленість у пізнанні нового, скрупульозність; Тип уроку : засвоєння нових […]...
- Системи рівнянь із двома змінними. Графічний метод розв’язання систем двох лінійних рівнянь із двома змінними 1007. Розв’язком системи рівнянь є пара чисел (6; 4), бо – правильні рівності. 1008. Пара чисел (-5; 2) є розв’язком системи рівнянь бо – правильні рівності. 1009. а) (1; 4) _ розв’язок системи рівнянь, бо 1 + 4 = 5 – правильна рівність; 3 • 1 + 4 = 7 – правильна рівність. Б) (-1; […]...
- Розв’язування логарифмічних рівнянь УРОК 58 Тема. Розв’язування логарифмічних рівнянь Мета уроку. формування умінь учнів розв’язувати логарифмічні рівняння різними методами: зведення логарифмічного рівняння до алгебраїчного; метод потенціювання; зведення логарифмів до однієї і тієї самої основи; метод логарифмування та графічний метод. І. Перевірка домашнього завдання 1. Усне розв’язування логарифмічних рівнянь з використанням таблиці 24 для усних обчислень “Логарифмічні рівняння”. 1 […]...
- Поняття про обернену функцію УРОК 17 Тема. Поняття про обернену функцію Мета уроку: формування понять: оборотна функція, обернена функція. Вивчення алгоритму знаходження формули функції, оберненої до даної, властивості графіків взаємно-обернених функцій. І. Аналіз контрольної роботи II. Сприймання і усвідомлення нового матеріалу На уроках математики ви неодноразово розв’язували задачу: обчислити значення функції у = f(x) при заданому значенні х0 аргументу. […]...
- Метод координат. Рівняння сфери, площини, прямої Завдання 2 1. 1) Рівняння сфери, усі точки якої рівновіддалені від початку координат на 1 од. має вигляд х2 + у2 + z2= 1. 2) Оскільки центр сфери – початок координат і вона перетинає ось Оz у точці (0; 0; 1), то вона має радіус 1, а значить, її рівняння; х2 + у2 + z2 […]...
- Запитання і вправи для повторення § 7 Відповідь: (3; 3), (-1; -2), (1; 0,5). 1012. а) х – 2y = 4; X 0 4 Y -2 0 Б) 4х + у = -4; X 0 -1 Y -4 0 В) 3х – 2y = 6. X 0 2 У -3 0 Відповідь: пара чисел (-2; 3) не являється розв’язком системи рівнянь Х […]...
- Розв’язування найпростіших тригонометричних рівнянь Математика – Алгебра Тригонометричні функції Розв’язування найпростіших тригонометричних рівнянь 1. cos x = a Розв’язки рівняння шукатимемо, спираючись на рисунок 1 або на рисунок 2. Якщо , розв’язків немає. , , . , , . , , . Рис. 2 Загальний випадок : , x = ±arccosa + 2πn,. У випадках, коли , , теж […]...
- 5 вправа 648-769 648. х – довжина сторони квадрата; S – площа квадрата; Х – незалежна змінна; у – залежна змінна. S = х2. 649. у = 5х; х – аргумент; у – функція. А) Якщо х = 2, то y = 5 • 2 = 10; якщо х = -1, то у = 5 • (-1) = […]...
- Системи двох лінійних рівнянь із двома змінними та графічний спосіб розв’язування систем Урок № 73 Тема. Системи двох лінійних рівнянь із двома змінними та графічний спосіб розв’язування систем Мета: засвоїти знання щодо залежності кількості розв’язків системи лінійних рівнянь від співвідношення коефіцієнтів a, b, c цих рівнянь; вироблення вмінь застосовувати названу ознаку під час графічного розв’язання систем рівнянь; подальше вдосконалювати вміння розв’язувати системи лінійних рівнянь графічним способом. Тип […]...