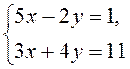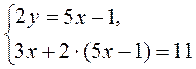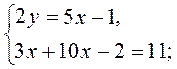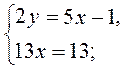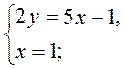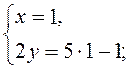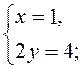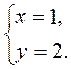Розв’язування систем лінійних рівнянь із двома змінними способом підстановки
Урок № 75
Тема. Розв’язування систем лінійних рівнянь із двома змінними способом підстановки
Мета: закріпити знання алгоритму розв’язування систем лінійних, рівнянь із двома змінними способом підстановки; вдосконалити вміння і навички, необхідні для застосування названого алгоритму; повторити матеріал попередньої теми щодо кількості розв’язків системи лінійних рівнянь залежно від співвідношення відповідних коефіцієнтів рівнянь.
Тип уроку: засвоєння вмінь та навичок.
Хід уроку
I. Організаційний момент
1.
2. Стан виконання домашнього завдання.
II. Перевірка домашнього завдання
@ Оскільки для розв’язання в домашньому завданні було запропоновано 4 системи, одну з яких треба було прокоментувати за алгоритмом, то роботу з перевірки домашнього завдання можна організувати так: учні розподіляються на і групи за номером завдання, яке вони коментували, і впродовж 3-5 хвилин обговорюють свої розв’язки і готують презентацію свого розв’язання. Через 5 хвилин кожна група презентує розв’язання, при цьому інші групи отримують завдання:
1) перевірити правильність виконання;
2)
III. Мотивація навчальної діяльності. Формулювання мети й завдань уроку
Пропонуємо спочатку для самостійного розв’язування систему:
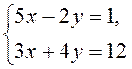 І даємо завдання:
І даємо завдання:
Порівняти із системами, запропонованими в домашньому завданні.
У чому збігаються?
(Відповідь. Жодного коефіцієнта, що дорівнював би ± 1.) Отже, після обговорення приходимо до необхідності вдосконалення вмінь щодо застосування алгоритму розв’язування систем рівнянь способом підстановки.
IV. Актуалізація опорних знань
Виконання усних вправ
1. Пара чисел є розв’язком рівняння х – 3у = 7. Знайдіть невідоме число в парі: (…; 6); (0; …); (-5; …); (…; 0).
2. В якій точці перетинаються прямі:
1) х – у = 3 та у = 3;
2) 5х + у = 4 та х – 0,2 = 0;
3) у = 0 та 6х – 11у = -18;
4) у = х та 3х – у = 0?
3. Перше рівняння системи у = х – 2. Підберіть для системи друге рівняння так, щоб ця система:
1) мала єдиний розв’язок; 2) не мала розв’язків.
4. Розв’яжіть систему:
1) 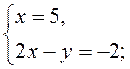 2)
2) 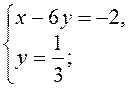 3)
3) 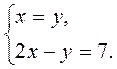
V. Удосконалення знань
@ На цьому уроці бажано провести роботу так, щоб учні ще раз усвідомили: 1) вибір змінної, що виключається з одного з рівнянь системи,- справа дуже відповідальна; 2) алгоритм розв’язування систем лінійних рівнянь із двома змінними способом підстановки можна дещо трансформувати (в п. 1), а саме: виразити не змінну, а її лінійну комбінацію (тобто, виражати не х, а 2х тощо). Найкраще все це робити, як і на попередньому уроці, на прикладі розв’язування конкретної системи.
Але спочатку звертаємось до № 3 домашнього завдання.
Якщо 2а = b + 1, то:
1) -2a = -(b + 1),
2) 4a = 2 – 2a = 2 – (b + 1);
3) 6a = 3 – 2a = 3(b + 1);
4) 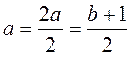 ;
;
5) 2a + 3 = (b + 1) + 3 = b +4.
Приклад (див. мотивація) | Коментар |
1. | 1. Оскільки жодний з коефіцієнтів змінних не дорівнює ± 1, а коефіцієнти при х пропорційні (кратні), то будемо виражати 2у з першого рівняння: 2у = 5х – 1. |
2. | 2. Оскільки 4у = 2 – 2у, то підставимо в друге рівняння замість 2у його вираз через х і дістанемо систему. |
3. Відповідь. (1; 2) | 3. Розв’яжемо друге рівняння системи. 4. Знайдемо відповідне значення другої змінної і запишемо відповідь |
@ Питання про розв’язування систем лінійних рівнянь, що не мають кратних коефіцієнтів при одній зі змінних або взагалі не мають виду лінійних рівнянь, також винесені на урок, і розв’язання цих питань пов’язано зі способами дій розв’язування рівнянь, що мають вид дробів із натуральними знаменниками.
Не забуваймо про рівносильні перетворення рівнянь.
VI. Вдосконалення вмінь
Виконання письмових вправ
1. Розв’яжіть систему рівнянь способом підстановки:
1) 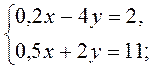 2)
2) 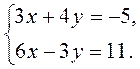
2. Розв’яжіть систему рівнянь:
1) 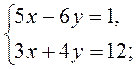
2) 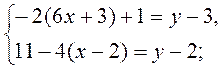
3) 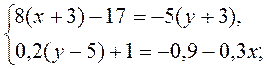
4) 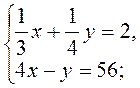
5) 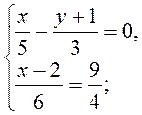
6) 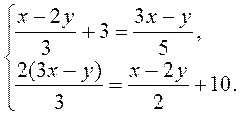
3. При яких значеннях а система рівнянь 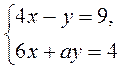 не має розв’язків?
не має розв’язків?
VII. Підсумок уроку
Розв’язати систему рівнянь, зробивши підстановку найзручнішим способом: 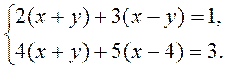
VIII. Домашнє завдання
Перетворивши кожне рівняння до вигляду ах + by = с, розв’яжіть систему рівнянь способом підстановки:
№ 1. 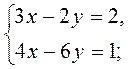
№ 2. 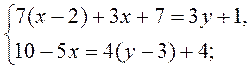
№ 3. 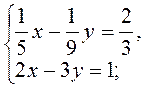
№ 4. 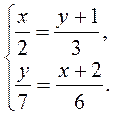
№ 5. Знайдіть НСК чисел: 1) 2 і 3; 2) 2 і 5; 3) 13 і 7; 4) 9 і 12.