Розв’язування систем лінійних рівнянь методом додавання
1047. 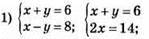
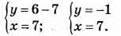
Відповідь: (7; -1).
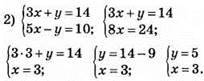
Відповідь: (3; 5).
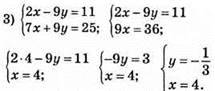
Відповідь: (4; -1/3).
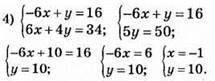
Відповідь: (-1; 10).
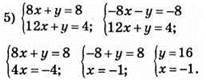
Відповідь: (-1; 16).
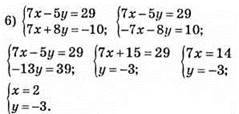
Відповідь: (2; -3).
1048. 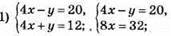
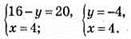
Відповідь: (4; -4).
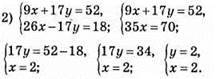
Відповідь: (2; 2).
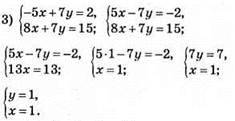
Відповідь: (1; 1).
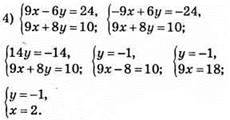
Відповідь: (2; -1).
1049.
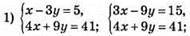
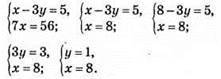
Відповідь: (8; 1).
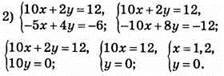
Відповідь: (1,2; 0).
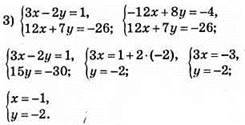
Відповідь: (-1; -2).
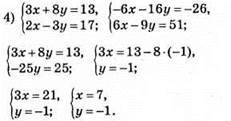
Відповідь: (7; -1).
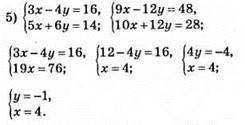
Відповідь: (4; -1).
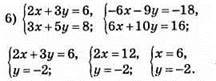
Відповідь: (6; -2).
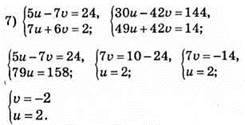
Відповідь: u = 2, v = -2.
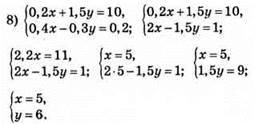
Відповідь: (5; 6).
1050. 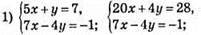
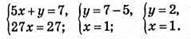
Відповідь: (1; 2).
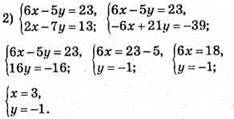
Відповідь: (3; -1).
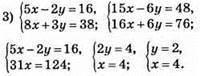
Відповідь: (4; 2).
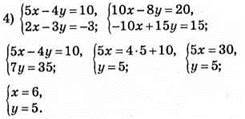
Відповідь:
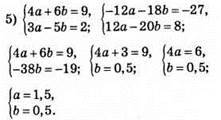
Відповідь: a = 1,5, b = 0,5.
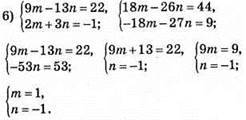
Відповідь: m = 1, n = -1.
1051. 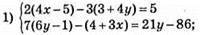
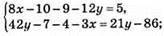
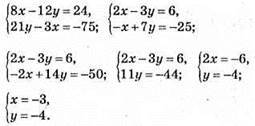
Відповідь: (-3; -4).
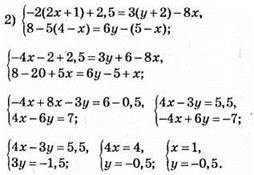
Відповідь: (1; -0,5).
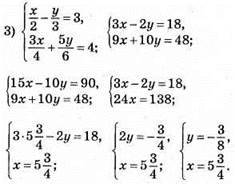
Відповідь: 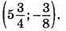
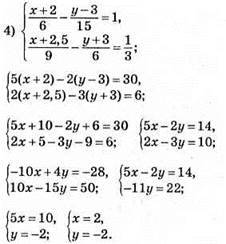
Відповідь: (2; -2).
1052. 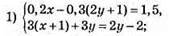
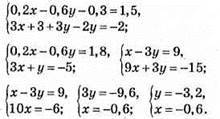
Відповідь: (-0,6; -3,2).
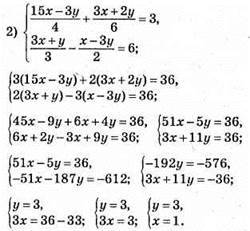
Відповідь: (1; 3).
1053. 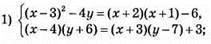
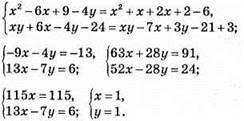
Відповідь: (1; 1).
2)
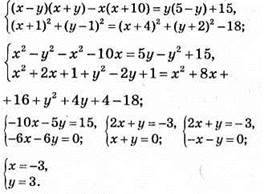
Відповідь: (-3; 3).
1054. 1)
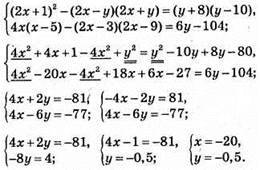
Відповідь: (-20; -0,5).
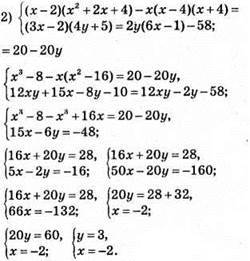
Відповідь: (-2; 3).
1055. 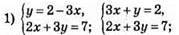
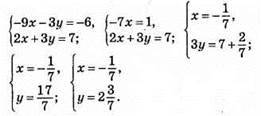
Відповідь: 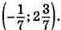
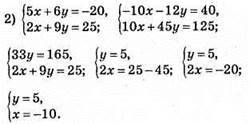
Відповідь: (-10; 5).
1056. 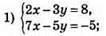
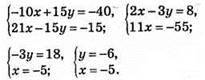
Відповідь: (-5; -6).
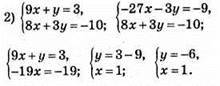
Відповідь: (1; -6).
1057. 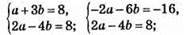
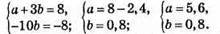
Відповідь: при а = 5,6; b = 0,8.
1058. 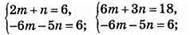
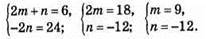
Відповідь: m = 9; n = -12.
1059. 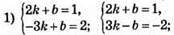
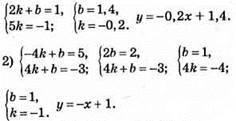
1060. 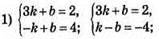
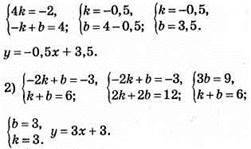
1061. 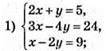
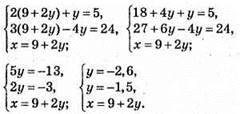
Система рівнянь розв’язків не має.
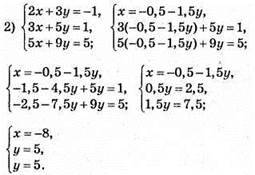
Відповідь: (-8; 5).
1062.
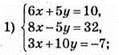
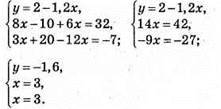
Відповідь: (3; -1,6).
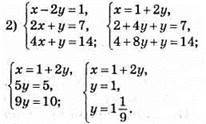
Система рівнянь розв’язків не має.
1063. 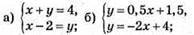
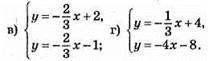
1064. 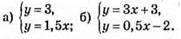
1065. 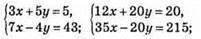
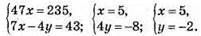
(5; -2) – точка перетину прямих 3х + 5y = 5 і 7х – 4y = 43.
У = kх + 2; -2 = 5k + 2; 5k = -4; k = -0,8; y = -0,8х + 2.
1066. 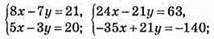
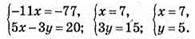
Ах + 2y = 24; 7 • а + 2 • 5 = 24; 7а = 24 – 10; 7а =14; а = 2.
Отже, при а = 2 система має розв’язок.
1067. 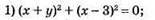
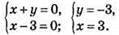
Відповідь: (3; -3).
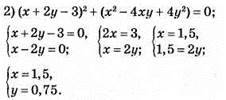
Відповідь: (1,5; 0,75).
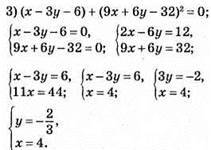
Відповідь: (4; -2/3).
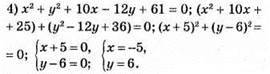
Відповідь: (-5; 6).
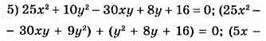
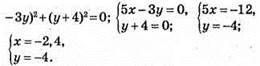
Відповідь:(-2,4; -4).
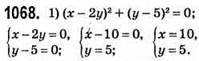
Відповідь: (10; 5).
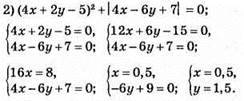
Відповідь: (0,5; 1,5).
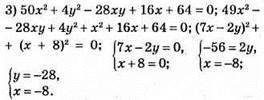
Відповідь: (-8; -28).
1069.
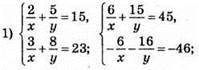
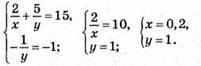
Відповідь: (0,2; 1).

Відповідь: (1; -1).
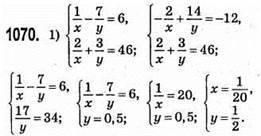
Відповідь: (1/20; 1/2).
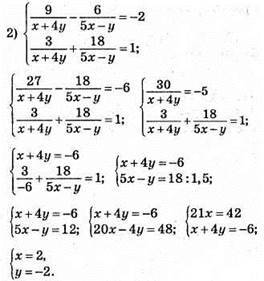
Відповідь; (2; -2).
1071. 1) Якщо а = -2, то 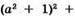
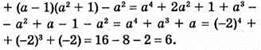
2) Якщо а = 1/2, то 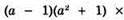
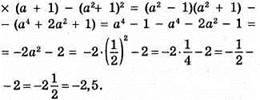
1072. Нехай учень розв’язав x задач і отримав за них 5x балів, тоді він не розв’язав (12 – x) задач і з нього зняли 3(12 – x) балів. За умовою 5x – 3(12 – x) = 36; 5x – 36 + 3x = 36; 8x = 72; x = 9 задач розв’язав учень.
1073. За 1 годину лев з’їсть 1 вівцю, вовк 1/3 вівці, собака 1/6 вівці. Разом за 1 годину вони з їдять 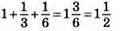 вівці. Тоді 3 вівці вони з’їдять за
вівці. Тоді 3 вівці вони з’їдять за 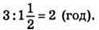
1074. Нехай 3n + 1 і 3n + 2 – довільні натуральні числа, які не діляться на 3.
Тоді (3n + 2)2 – (3n + 1)2 = (3n + 2 – 3n – 1) • (3n + 2 + 3n + 1) = 6n + 3 – 3(2n + 1) – кратне 3.
1075. Кількість дерев більша за 90, але менша за 100. Крім того, це число повинне ділитися на З і на 4. Це число 96.
1076. 1) – x2 – 4x + 6 = -(x2 + 4х – 6) = -(х2 + 4х + 4 – 10) = -(х + 2)2 + 10. Вираз може набувати і від’ємних, і додатних значень.
2) – x2 + 16x – 64 = -(x2 – 16x + 64) = -(х – 8)2. Вираз може набувати лише недодатних значень.
3) – x2 + 8x -18 = -(x2 – 8х + 18) = -(х2 – 8x + 16 + 2) = -(х – 4)2 – 2. Вираз може набувати лише від’ємних значень.