Симетрія відносно точки
УРОК № 34
Тема. Симетрія відносно точки
Мета уроку: формування поняття симетрії відносно точки; вивчення властивостей симетрії відносно точки; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач.
Тип уроку: комбінований.
Наочність і обладнання: таблиця “Перетворення фігур. Рухи” [13].
Вимоги до рівня підготовки учнів: описують симетрію відносно точки; будують фігури, у які переходять дані фігури при симетрії відносно точки; наводять приклади фігур, які мають центр симетрії; застосовують
Хід уроку
I. Перевірка домашнього завдання
Перевірити наявність виконаних домашніх завдань та відповісти на запитання, які виникли в учнів при їх виконанні.
Фронтальне опитування
1) Яке перетворення фігури називається переміщенням? 2) Доведіть, що під час руху точки, які лежать на прямій, переходять у точки, які також лежать на прямій, і зберігається порядок їх взаємного розміщення. 3) У що переходять прямі, півпрямі, відрізки при переміщенні? 4) Доведіть, що при переміщенні зберігаються кути. 5) Периметри двох ромбів рівні. Чи випливає
II. Поетапне сприймання й усвідомлення нового матеріалу
Поняття симетрії відносно точки
Перетворення фігур за допомогою переміщення має декілька видів. Сьогодні ми ознайомимося з перетворенням фігури за допомогою симетрії відносно точки.
Точки X і X1 називаються симетричними відносно точки О, якщо точка О є серединою відрізка ХХ1 (рис. 160).
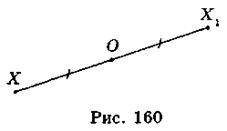
Точка О називається центром симетрії. Перетворення фігури F на фігуру Ft, при якому кожна точка X фігури F переходить у точку Х1 фігури F1, симетричну точці X відносно даної точки О, називається перетворенням симетрії відносно точки О. Фігури F і F1 називаються центральносиметричними (симетричними відносно точки О) (рис. 161).
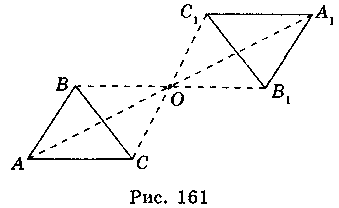
Властивості симетрії відносно точки (центральної симетрії)
1) Перетворення симетрії відносно точки є переміщенням. 2) Перетворення симетрії відносно точки перетворює пряму на паралельну їй пряму або на себе; відрізок – на рівний і паралельний йому відрізок; многокутник – на рівний йому многокутник. 3) Будь-яка пряма, що проходить через центр симетрії, відображається при цій симетрії на себе. Якщо перетворення симетрії відносно точки О переводить фігуру F (рис. 162) у себе, то вона називається центральносиметричною, а точка О – центром симетрії.
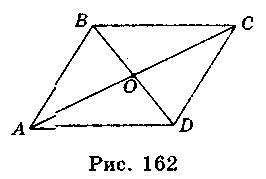
Якщо точка А(х;у) симетрична точці В(х1; у1) відносно початку координат О, то виконуються умови 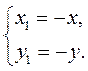
Виконання вправ
1. Побудуйте довільний трикутник ABC. Побудуйте трикутник, симетричний побудованому відносно точки:
А) А;
Б) В;
В) яка лежить зовні трикутника;
Г) яка лежить усередині трикутника.
2. Побудуйте чотирикутник ABCD, у якого А(1; 1), В(-1; 1), С(1; 3) і D(-1; 3). Побудуйте чотирикутник, який симетричний побудованому чотирикутнику відносно точки О.
III. Закріплення й осмислення навчального матеріалу
Виконання вправ
1. Доведіть властивості симетрії відносно точки. 2. Запишіть рівняння кола, яке симетричне колу (х – 1)2 + (у + 2)2 = 1 відносно початку координат. 3. Запишіть рівняння прямої, яка симетрична прямій х + у = 1 відносно початку координат. 4. Дано дві прямі, які перетинаються, і точка О, що лежить між ними. Побудуйте відрізок з кінцями на даних прямих і серединою в даній точці.
IV. Домашнє завдання
1. Вивчити теоретичний матеріал. 2. Розв’язати задачі. 1) Доведіть, що у паралелограма точка перетину діагоналей є центром симетрії. 2) Доведіть, що чотирикутник, у якого є центр симетрії, є паралелограмом.
V. Підбиття підсумків уроку
Запитання до класу
1. Які точки називаються симетричними відносно даної точки? 2. Які перетворення називаються симетрією відносно даної точки? 3. Яка фігура називається центральносиметричною? 4. Що таке центр симетрії фігури? Наведіть приклади центральносиметричних фігур.