Системи рівнянь – РІВНЯННЯ
Формули й таблиці
МАТЕМАТИКА
РІВНЯННЯ
Лінійне рівняння з однією змінною – рівняння, що зводиться до канонічного вигляду ах + b = 0, де х – змінна, а й b – константи.
Корінь рівняння ах + b = 0 визначається формулою: х = – b/а
– якщо а ≠ 0, множина розв’язків L = {-b/a}.
– якщо а = 0, b = 0 , тоді коренів безліч;
– якщо а = 0, b ≠ 0 , тоді рівняння не має коренів.
Лінійне рівняння із двома змінними – рівняння, що зводиться до канонічного вигляду ах + by + с = 0, де х та у – змінні, а і b – константи. Лінійне рівняння
Лінійне рівняння із двома змінними – це рівняння прямої, воно визначає на координатній площині хОу пряму, координати (х; у) кожної точки якої є розв’язком цього рівняння. Цю пряму називають графіком, або геометричною моделлю.
Для побудови графіка Л. р. із двома змінними треба знайти два його розв’язки: (х1;у1) і (х2;у2), побудувати на координатній
Системи рівнянь
Система лінійних рівнянь:
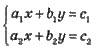
1. Має один розв’язок, якщо
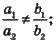
Коефіцієнти х і у непропорційні; прямі перетинаються.
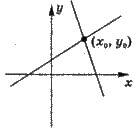
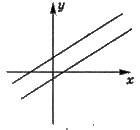
2. Не має розв’язків, якщо
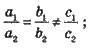
Прямі паралельні.
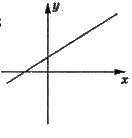
3. Має безліч розв’язків, якщо
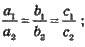
Прямі співпадають.
Related posts:
- Графік лінійного рівняння з двома невідомими – Системи лінійних рівнянь Математика – Алгебра Системи лінійних рівнянь Графік лінійного рівняння з двома невідомими Графіком рівняння з двома невідомими називається множина всіх точок координатної площини, координати котрих є розв’язками цього рівняння. Графіком рівняння , у якому хоча б один із коефіцієнтів (a або b) відмінний від нуля, є пряма. Для побудови будь-якої прямої досить знати координати двох […]...
- Рівняння з двома змінними – Системи лінійних рівнянь Математика – Алгебра Системи лінійних рівнянь Рівняння з двома змінними Лінійним рівнянням з двома невідомими Називається рівняння виду , де x і y – невідомі, a, b, і с – числа (Коефіцієнти рівняння). Розв’язком рівняння з двома невідомими називається пара значень невідомих, при яких рівняння перетворюється у правильну числову рівність. Наприклад: ; – розв’язок рівняння, […]...
- Лінійне рівняння з двома змінними та його графік Урок № 70 Тема. Лінійне рівняння з двома змінними та його графік Мета: формувати свідоме розуміння означення лінійного рівняння з двома змінними та вигляду графіка лінійного рівняння з двома змінними (зокрема, його особливих видів); виробляти вміння: відрізняти лінійне рівняння з двома змінними з-поміж інших рівнянь; будувати графіки лінійних рівнянь із двома змінними; подальше вдосконалювати вміння […]...
- Системи лінійних рівнянь з двома невідомими – Системи лінійних рівнянь Математика – Алгебра Системи лінійних рівнянь Системи лінійних рівнянь з двома невідомими Якщо треба знайти спільні розв’язки кількох рівнянь, то кажуть, що ці рівняння утворюють Систему рівнянь. Розв’язок системи рівнянь з двома невідомими – пара значень невідомих, яка є розв’язком кожного з рівнянь системи. Розв’язати систему рівнянь означає знайти всі її розв’язки або довести, що […]...
- Системи рівнянь з двома змінними. Графічний спосіб розв’язування систем рівнянь з двома змінними УРОК № 30 Тема. Системи рівнянь з двома змінними. Графічний спосіб розв’язування систем рівнянь з двома змінними Мета уроку: закріпити знання учнів про зміст означень: графік рівняння з двома змінними, система рівнянь з двома змінними, розв’язок системи рівнянь з двома змінними, а також алгоритмів побудови графіка рівняння з двома змінними та графічного способу розв’язування системи […]...
- ПОВТОРЕННЯ. РОЗВ’ЯЗУВАННЯ РІВНЯНЬ І ЗАДАЧ Цілі: – навчальна: узагальнити та систематизувати знання учнів про види рівнянь, їх систем і способи їх розв’язання; – розвивальна: формувати вміння аналізувати й узагальнювати інформацію, бачити закономірності; розвивати увагу, логічне мислення, пам’ять; – виховна: виховувати відповідальність за результати своєї роботи, наполегливість у досягненні мети, віру у власні сили; Тип уроку : узагальнення та систематизація знань. […]...
- Лінійне рівняння з двома змінними і його графік Урок № 71 Тема. Лінійне рівняння з двома змінними і його графік Мета: вдосконалювати уміння перетворювати лінійні рівняння з двома змінними та знаходити їх розв’язки, а також будувати графіки лінійних рівнянь із двома змінними (залежно від значень а, b, с), працювати з графіками; здійснити діагностику засвоєння основних понять і вмінь, передбачених програмою за темою “Рівняння […]...
- Лінійне рівняння з однією змінною. Розв’язування лінійних рівнянь з однією змінною і рівнянь, що зводяться до них Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ & 23. Лінійне рівняння з однією змінною. Розв’язування лінійних рівнянь з однією змінною і рівнянь, що зводяться до них Ми знаємо, як розв’язувати рівняння 2х = -8; х – 5; 0,01х -17. Кожне із цих рівнянь має вигляд ах = b, де х – змінна, а і b […]...
- Лінійні рівняння з одним невідомим Математика – Алгебра Рівняння Лінійні рівняння з одним невідомим Рівняння виду , де a і b – деякі числа, а х – невідоме, називається Лінійним рівнянням з одним невідомим. Числа a і b називають Коефіцієнтами. Кількість коренів лінійного рівняння 1. Якщо , лінійне рівняння має єдиний корінь: . 2. Якщо , , лінійне рівняння коренів […]...
- Розв’язування найпростіших тригонометричних рівнянь. Рівняння sin t = a УРОК 21 Тема. Розв’язування найпростіших тригонометричних рівнянь. Рівняння sin t = а Мета уроку: засвоєння учнями виведення і застосування формули для коренів рівняння sin t = а. Обладнання: Таблиця “Рівняння sin t = а”. І. Перевірка домашнього завдання 1. Відповіді на питання, що виникли при виконанні домашніх завдань. 2. Самостійна робота. Варіант 1 Розв’яжіть рівняння: […]...
- РІВНЯННЯ. ВЛАСТИВОСТІ РІВНОСИЛЬНОСТІ РІВНЯНЬ РОЗДІЛ 5 ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ У розділі дізнаєтесь: ► які рівняння називають рівносильними; ► про властивості рівносильності рівнянь; ► що таке лінійне рівняння з однією змінною; ► які особливості лінійного рівняння з двома змінними; ► про графік лінійного рівняння із двома змінними; ► що таке система двох лінійних рівнянь із двома змінними; ► […]...
- Розв’язування найпростіших тригонометричних рівнянь. Рівняння cos t = a УРОК 20 Тема. Розв’язування найпростіших тригонометричних рівнянь. Рівняння cos T = a Мета уроку: засвоєння учнями виведення і застосування формули для знаходження коренів рівняння cos t = a. Обладнання: Таблиця “Рівняння cos t = a”. І. Перевірка домашнього завдання Математичний диктант Обчисліть: 1) arcsin ; 2) arcos ; 3) arctg ; 4) arcsin; 5) arccos; […]...
- Підсумковий урок з теми “Системи рівнянь з двома змінними” УРОК № 37 Тема. Підсумковий урок з теми “Системи рівнянь з двома змінними” Мета уроку: повторити, систематизувати й узагальнити знання та вміння учнів щодо змісту вивчених у розділі “Системи рівнянь з двома змінними вищих степенів” понять і схем розв’язування типових задач шляхом складання загальних алгоритмів розв’язування задач. Провести корекційну роботу з метою усунення причин найтиповіших […]...
- ЛІНІЙНІ РІВНЯННЯ ТА їХ СИСТЕМИ ЯК МАТЕМАТИЧНІ МОДЕЛІ ТЕКСТОВИХ ЗАДАЧ. РОЗВ’ЯЗУВАННЯ ЗАДАЧ ЗА ДОПОМОГОЮ ЛІНІЙНИХ РІВНЯНЬ Цілі: – навчальна: сформувати уявлення про прикладні задачі та математичні моделі задач; сформувати вміння складати та розв’язувати рівняння, що є математичними моделями прикладних текстових задач; домогтися засвоєння схеми розв’язання задач за допомогою лінійних рівнянь; – розвивальна: розвивати увагу, логічне мислення, пам’ять; формувати вміння вибирати і використовувати необхідну інформацію для розв’язування задач; – виховна: виховувати інтерес […]...
- Система двох лінійних рівнянь із двома невідомими – РІВНЯННЯ Формули й таблиці МАТЕМАТИКА РІВНЯННЯ Система двох лінійних рівнянь із двома невідомими – сталі. Правило Крамера: Квадратний тричлен – тричлен виду у = ах2 + bх + с, де х – змінна, а, b, с – константи і а ≠ 0. Одночлен ах2 називають старшим членом квадратного тричлена, а коефіцієнт а – старшим коефіцієнтом. Квадратний […]...
- Розв’язування найпростіших тригонометричних рівнянь. Рівняння tg t = a УРОК 22 Тема. Розв’язування найпростіших тригонометричних рівнянь. Рівняння tg T = a. Мета уроку: зсвоєння учнями виведення і застосування формули для знаходження коренів рівняння tg t = a (ctg t = а). Обладнання: Таблиця “Рівняння tg t = а і ctg t = a”. І. Перевірка домашнього завдання 1. Перевірити наявність домашніх завдань в зошитах […]...
- Поняття рівняння. Розв’язування рівнянь 770. а) 5х = 3х + 4. Х = 2 – корінь рівняння, бo 5 • 2 = 3 • 2 + 4 – правильна рівність. Б) 2х + 8 = 7х. Х = 2 – не є коренем рівняння, 2 • 2 + 8 = 7 • 2 – неправильна рівність. В) 10 – […]...
- Система двох лінійних рівнянь з двома змінними та її розв’язок. Розв’язування систем лінійних рівнянь з двома змінними графічно Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ & 27. Система двох лінійних рівнянь з двома змінними та її розв’язок. Розв’язування систем лінійних рівнянь з двома змінними графічно Приклад 1. Маска й трубка для підводного плавання разом коштують 96 грн, причому маска на 16 грн дорожча за трубку. Скільки коштує маска і скільки трубка? Р о […]...
- Системи рівнянь з двома змінними УРОК 64 Тема. Системи рівнянь з двома змінними Тестові завдання 1. Яка з пар чисел є розв’язком рівняння 3х2 – 2ху +1 = 0 ? А) (1; 2); б) (2; 2); в) (0; 3); г) (0;0)? 2. Яка з пар чисел є розв’язком системи А) (3; 0); б) (2; 1); в) (1; 2); г) (0; […]...
- Рівняння прямої УРОК № 28 Тема. Рівняння прямої Мета уроку: виведення рівняння прямої. Формування вмінь учнів використовувати рівняння прямої до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати і вектори на площині” [13]. Вимоги до рівня підготовки учнів: записують і пояснюють рівняння прямої. Розпізнають рівняння прямої. Хід уроку I. Перевірка домашнього завдання Перевірити наявність […]...
- Рівняння з двома змінними 909. Рівняннями з двома змінними є рівняння; 1), 3), 5), 6), 8), 9). 910. 1) 4x + 3y = 1; 4 • (-2) + 3 • 3 = 1 – правильна рівність, тому (-2; 3) – розв’язок даного рівняння. 2) x2 + 5 = у2; (-2)2 + 5 = 32 – правильна рівність, тому (-2; […]...
- Розділ 5. Лінійні рівняння та їх системи Рівносильні, бо корені однакові. Не рівносильні, бо корені різні. – один корінь; – коренів немає. 5. Нехай у 7-Б класі навчається х учнів, тоді у 7-А класі навчається (х + 3) учнів. Оскільки загальна кількість учнів у 7-А та 7-Б дорівнює 55, складемо та розв’яжемо рівняння: Х + х + 3 = 55; 2х = […]...
- Графік рівняння з двома змінними УРОК № 28 Тема. Графік рівняння з двома змінними Мета уроку: домогтися засвоєння учнями змісту: означення графіка рівняння з двома змінними; схеми дій для побудови графіка рівняння з двома змінними. Виробити вміння: відтворювати зміст вивченого означення та алгоритму; застосовувати їх для розв’язування вправ на побудову графіків рівнянь з двома змінними. Тип уроку: узагальнення та систематизація […]...
- Рівняння кола УРОК № 26 Тема. Рівняння кола Мета уроку: виведення рівняння кола. Формування вмінь учнів використовувати рівняння кола до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати і вектори на площині” [13]. Вимоги до рівня підготовки учнів: записують і пояснюють рівняння кола. Розпізнають рівняння кола. Хід уроку I. Перевірка домашнього завдання Перевірити наявність […]...
- ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ РОЗДІЛ 5 ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ &22. ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ Ви знаєте, що кожній упорядкованій парі чисел відповідає певна точка на координатній площині. Оскільки кожний розв’язок рівняння з двома змінними х і у – це упорядкована пара чисел, то всі його розв’язки можна зобразити точками па координатній площині. У цих точок […]...
- СИСТЕМА ДВОХ ЛІНІЙНИХ РІВНЯНЬ ІЗ ДВОМА ЗМІННИМИ РОЗДІЛ 5 ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ &23. СИСТЕМА ДВОХ ЛІНІЙНИХ РІВНЯНЬ ІЗ ДВОМА ЗМІННИМИ Ви вже знаєте, як розв’язати задачу за допомогою лінійного рівняння з однією змінною. За допомогою лінійних рівнянь із двома змінними також можна розв’язувати задачі. Розглянемо приклад. Задача 1. Сума двох чисел дорівнює 3, а різниця подвоєного першого числа і потроєного […]...
- Рівняння із двома змінними та його розв’язок Урок № 69 Тема. Рівняння із двома змінними та його розв’язок Мета: сформувати уявлення про рівняння із двома змінними та його розв’язки; усвідомити зміст поняття “графік рівняння із двома змінними”; виробити вміння: відбирати перевіркою розв’язки рівняння із двома змінними; працювати з готовим графіком рівняння із двома змінними; перетворювати рівняння виду у = f(x) та обчислювати […]...
- Лінійні рівняння та їх системи 831. 3) 7х – 2 = 10; 1), 2), 4) – не є рівняннями. 832. 1) 2х = 6; х = 3 – корінь рівняння; 4) 27 : х = 9; х = 3 – корінь рівняння. 833. 1) х + 7 = 9; х = 2 – розв’язок; 3) х – 8 = -6; […]...
- Система двох лінійних рівнянь із двома змінними та її розв’язок Урок № 72 Тема. Система двох лінійних рівнянь із двома змінними та її розв’язок Мета: сформувати уявлення учнів про розв’язок системи рівнянь із двома змінними та графічний спосіб розв’язання систем лінійних рівнянь; виробити вміння: здійснювати перевірку, чи є пара (х; у) розв’язком даної системи лінійних рівнянь; використовуючи навички побудови графіка лінійного рівняння з двома змінними, […]...
- Системи двох лінійних рівнянь із двома змінними та графічний спосіб розв’язування систем Урок № 73 Тема. Системи двох лінійних рівнянь із двома змінними та графічний спосіб розв’язування систем Мета: засвоїти знання щодо залежності кількості розв’язків системи лінійних рівнянь від співвідношення коефіцієнтів a, b, c цих рівнянь; вироблення вмінь застосовувати названу ознаку під час графічного розв’язання систем рівнянь; подальше вдосконалювати вміння розв’язувати системи лінійних рівнянь графічним способом. Тип […]...