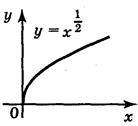
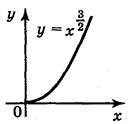
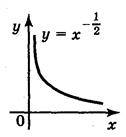
Степенева функція
УРОК 41
Тема. Степенева функція
Мета уроку. Познайомити учнів із степеневою функцією, її властивостями і графіками.
І. Перевірка домашнього завдання
1. Перевірити наявність виконаного домашнього завдання.
2. Розв’язування вправ.
А) Обчислити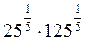 
. Відповідь: 5.
Б) Спростити вираз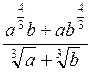 
. Відповідь: ab.
В) Спростити вираз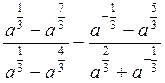 
. Відповідь: 2a.
II. Сприймання і усвідомлення матеріалу про степеневу функцію
Степеневою функцією називається функція виду у = хp, де
Функція у = хp
P | D(y) | E(y) | Парність (непарність) | Зростання (спадання) | ||
1. | P=2k, K |
| R | [0; + | Парна | Спадає, якщо Х Якщо х |
2. | P=2k+1 K |
| R | R | Непарна | Зростає |
3. | P=-(2k), K |
| X? 0 | (0; + | Парна | Зростає, якщо Х Якщо х |
4. | P=-(2k-1) K |
| X? 0 | Y? 0 | Непарна | Спадає На проміжках (- (0; + |
5. | P > 0, p – не ціле, 0<р<1 |
| [0;+ | [0;+ | Ні парна, Ні непарна | Зростає |
6. | Р>0, P – не ціле, Р > 1 |
| [0;+ | [0;+ | Ні парна, Ні непарна | Зростає |
7. | Р < 0, Р – не Ціле |
| (0;+ | (0;+ | Ні парна, Ні непарна | Спадає |
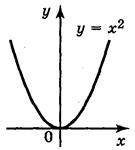
1. Якщо р = 2k, k 
Z, то функція у = х2k. Якщо k = 1, то ця функція має вигляд у = х2. Згадаємо її основні властивості. Функція у = х2:
– визначена для будь-якого дійсного х;
– додатна при х? 0 і дорівнює 0 при х = 0;
– приймає всі невід’ємні значення;
– парна (графік симетричний відносно осі OY);
– спадає, якщо х є (-
; 0] і зростає, якщо х є [0; +). Такі саме властивості має. функція у = х2k (рис. 80 підручника).
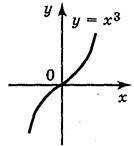
2. Якщо р = 1, то функція має вигляд у = х (графік – пряма, що проходить через початок координат і ділить перший і третій координатний кути пополам). Якщо р = 3, то ця функція має вигляд у = х3. Функція у = х3:
– визначена для будь-якого дійсного х;
– додатна при х > 0, від’ємна при х < 0 і дорівнює 0 при х = 0;
– зростаюча;
– приймає всі дійсні значення;
– непарна (графік симетричний відносно початку координат), Такі самі властивості має степенева функція у = х2k+1, kN (рис. 79 підручника).
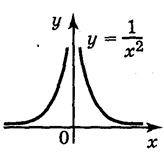
3. Розглянемо функцію у =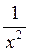 
. Ця функція визначена при х? 0 і приймає всі додатні значення. Функція парна (графік симетричний відносно осі OY). При х < 0 функція зростає, а при х > 0 – спадає. Такі саме властивості має степенева функція у = х-2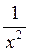k =, kN (рис. 82 підручника).
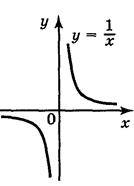
4. Якщо р = – 1, то функція має вигляд у = х-1 =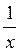 
. Ця функція визначена при х? 0. При х > 0 функція у = 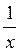приймає додатні значення, а при х < 0 – від’ємні. При х > 0 функція у = 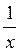спадає, і при х < 0 – спадає.
Такі саме властивості має степенева функція у = х – (2k – 1) =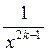 
, kN (рис. 81 підручника).
5-6. Згадаємо властивості функції у =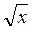 
. Отже, функція у = :
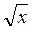– визначена при х > 0;
– додатна при х > О і дорівнює нулю при х = 0;
– зростає на всій області визначення;
– приймає всі невід’ємні значення.
Якщо р – додатне раціональне число, то степенева функція у = xp визначена при х 
0 і має такі саме властивості, які функція у = .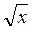
III. Осмислення вивченого матеріалу
Виконання № 78-85 із “Запитання і завдання для повторення” розділу III.
IV. Підсумок уроку
V. Домашнє завдання
Розділ III § 3(4). Запитання і завдання для повторення розділу III. № 67-77. Підготуватися до контрольної роботи.
(1 votes, average: 5.00 out of 5)
Loading...