Головна ⇒ 👍Формули й таблиці ⇒ Степінь з раціональним показником – СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ


Степінь з раціональним показником – СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ


Формули й таблиці

МАТЕМАТИКА

СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ

Степінь з раціональним показником

N )

Для будь-якого невід’ємного числа а й натурального числа n (n ≥ 2) існує одне невід’ємне число b, при якому bn = а й позначається 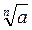Степінь з раціональним показником СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ .

Звідси випливає:

1. 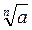Степінь з раціональним показником СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ = 0 тільки при а = 0;

2. 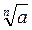Степінь з раціональним показником СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ = 1 тільки при а = 1;

3. Якщо а ≥ 0, то арифметичний корінь 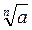Степінь з раціональним показником СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ ≥ 0.

Невід’ємний корінь парного степеня n з числа а називається арифметичним й позначається 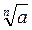Степінь з раціональним показником СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ .

Якщо n – парне число, то b = 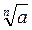Степінь з раціональним показником СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ тоді й тільки тоді, коли

Степінь з раціональним показником СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ

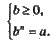
Якщо ж n – непарне число, то для будь-якого а існує тільки один корінь степеня n із числа а. Він і позначається через 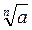Степінь з раціональним показником СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ. Таким чином, якщо n – непарне число, то b = 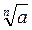Степінь з раціональним показником СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ тоді й тільки тоді, коли bn = а.



1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5,00 out of 5)



Що таке ланцюжок живлення.

Related posts:

  1. Властивості степеня з цілим показником – СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Формули й таблиці МАТЕМАТИКА СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Степінь числа з натуральним показником n – добуток Позначуване аn; число а називається основою, а натуральне число n > 1 – показником степеня. Степінь числа з натуральним показником n називають n-м степенем числа а. Другий степінь числа називають квадратом цього числа. Степінь числа з нульовим показником – вираз […]...

  2. Основні властивості кубічного кореня – СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Формули й таблиці МАТЕМАТИКА СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Основні властивості кубічного кореня Для будь-яких дійсних чисел a й b: 1) а = ()3; 2) = а; 3) = ; 4) якщо b ≠ 0, то ; 5) = тільки тоді, коли а = b; 6) < тільки тоді, коли а < b; 7) < тільки тоді, […]...

  3. Основні властивості арифметичного квадратного кореня – СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Формули й таблиці МАТЕМАТИКА СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Основні властивості арифметичного квадратного кореня Для будь-яких дійсних чисел а й b: 1) якщо а ≥ 0, , то а = ()2; 2) = |a|; 3) якщо а ≥ 0 й b ≥ 0, то = ; 4) якщо а ≥ 0 й b > 0, то ; […]...

  4. Степінь з натуральним показником Математика – Алгебра Одночлени Степінь з натуральним показником Степенем Числа a з натуральним показником n, більшим за 1, називається добуток n множників, кожний із яких дорівнює a. Тобто де a – основа степеня; n – показник степеня. Степенем числа a з показником 1 є са­­ме число a. Знак степеня з натуральним показником 1. Якщо основа […]...

  5. Степінь з натуральним показником Урок № 20 Тема. Степінь з натуральним показником Мета: розширити знання учнів відомостями про властивості степенів раціональних чисел з парним та непарним показником; сформувати вміння застосовувати ці властивості під час розв’язування вправ. Тип уроку: застосування знань, умінь та навичок. Хід уроку І. Перевірка домашнього завдання @ № 1-2 – вправи на відтворення вмінь, набутих на […]...

  6. Кoрінь n-го степеня та його властивості Математика – Алгебра Степенева функція Кoрінь n-го степеня та його властивості Коренем N-го степеня з числаА називається таке число, n-й степінь якого дорівнює а. Якщо n – число непарне, то існує – і до того ж тільки один – корінь n-го степеня з довільного числа а. Цей корінь – число того ж знака, що число […]...

  7. СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ РОЗДІЛ II ОДНОЧЛЕНИ &5. СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ Подивіться на малюнки 3 і 4. Ви бачите квадрат зі стороною а (мал. 3) і куб з ребром а (мал. 4). Ви знаєте, як знайти площу квадрата й об’єм куба та як записати результат за допомогою відповідних виразів: а2 і а3. Узагалі, добуток n рівних множників, кожний […]...

  8. Степінь натурального числа з натуральним показником Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 7. Степінь натурального числа з натуральним показником Уже відомо, що суму, в якій всі доданки рівні між собою, можна записати коротше – у вигляді добутку. Наприклад, У математиці є спеціальний спосіб і для запису добутку, в якому всі множники рівні між собою. […]...

  9. ПОВТОРЕННЯ. СТЕПІНЬ НАТУРАЛЬНОГО ЧИСЛА З НАТУРАЛЬНИМ ПОКАЗНИКОМ. ПЛОЩІ ТА ОБ’ЄМИ ФІГУР Цілі: – навчальна: повторити поняття степеня натурального числа з натуральним показником; узагальнити знання учнів про площі та об’єми фігур; відтворити вміння розв’язувати задачі на обчислення площі прямокутника і квадрата, об’єму прямокутного паралелепіпеда і куба; – розливальна: формувати вміння аналізувати й узагальнювати інформацію; – виховна: виховувати відповідальність, свідоме ставлення до навчання; Тип уроку: узагальнення та систематизація […]...

  10. Властивості степеня з натуральним показником (продовження). Степінь степеня Урок № 23 Тема. Властивості степеня з натуральним показником (продовження). Степінь степеня Мета: свідоме засвоїти зміст властивостей піднесення степеня до степеня, виробляти вміння виконувати перетворення виразів із застосуванням раніше набутих знань про властивості степеня в комплексі з названою властивістю; систематизувати знання учнів про властивості степеня. Тип уроку: засвоєння знань, умінь та навичок. Хід уроку I. […]...

  11. Степінь з натуральним показником. Одночлен Урок № 30 Тема. Степінь з натуральним показником. Одночлен Мета: діагностика рівня набутих знань та вмінь учнів з теми. Тип уроку: контроль знань, умінь, навичок. Хід уроку І. Умова тематичної контрольної роботи Варіант 1 Варіант 2 № 1. Знайдіть значення виразу: 1) 1,5 • 62 – 24; 2) 1) 2,5 • 25 – 72; 2) […]...

  12. Степінь з натуральним показником та властивості степеня з натуральним показником Урок № 25 Тема. Степінь з натуральним показником та властивості Степеня з натуральним показником Мета: повторити, систематизувати та узагальнити знання учнів про означення та властивості степеня числа з натуральним показником; відпрацювати та вдосконалити вміння і навички щодо застосування названих теоретичних відомостей для спрощення виразів та виконання обчислень; здійснити проміжну діагностику засвоєних знань та вмінь у […]...

  13. Степінь з натуральним показником. Одночлени Урок № 29 Тема. Степінь з натуральним показником. Одночлени Мета: узагальнити та систематизувати знання та вміння учнів, набуті в ході вивчення названої теми, підготовити учнів до тематичного оцінювання. Обладнання: таблиця “Степінь. Властивість степеня”. Тип уроку: узагальнення та систематизація знань та вмінь. Хід уроку I. Перевірка домашнього завдання @ Цей етап уроку є ще аналізом самостійної […]...

  14. Підсумковий урок з теми “Степінь з від’ємним цілим показником. Стандартний вигляд числа” Урок № 31 Тема. Підсумковий урок з теми “Степінь з від’ємним цілим показником. Стандартний вигляд числа” Мета: повторити, систематизувати та узагальнити знання і способи дій, які опанували учні під час вивчення теми “Степінь з цілим від’ємним показником. Стандартний вигляд числа”. Тип уроку: систематизація та узагальнення знань і вмінь. Наочність та обладнання: опорні конспекти. Хід уроку […]...

  15. СТЕПІНЬ НАТУРАЛЬНОГО ЧИСЛА З НАТУРАЛЬНИМ ПОКАЗНИКОМ. ПЛОЩІ ТА ОБ’ЄМИ ФІГУР ЗАДАЧІ НА ПОВТОРЕННЯ СТЕПІНЬ НАТУРАЛЬНОГО ЧИСЛА З НАТУРАЛЬНИМ ПОКАЗНИКОМ. ПЛОЩІ ТА ОБ’ЄМИ ФІГУР 50. Обчисліть: 1)5 ∙ 26 + 22 – 4 ∙З4; 3) б2: 2 ∙ (43-55); 2) 2(2 ∙ 53- 102): 52; 4) 23: 12 ∙ 53-(32 ∙ 5-5). 51. Знайдіть значення виразу а3+ b2, якщо: 1) а = 2, b= 12; 2)а=1,b=1; […]...

  16. Степінь числа Розділ I НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ § 3. МНОЖЕННЯ І ДІЛЕННЯ НАТУРАЛЬНИХ ЧИСЕЛ 20. Степінь числа Як ви знаєте, за допомогою добутку зручно записувати суму кількох рівних доданків. Наприклад, 7+7+7 + 7 = 7∙4. У математиці придумали спосіб коротко записувати добуток, у якому всі множники рівні. Наприклад, 7 ∙ 7 ∙ 7 ∙ […]...

  17. ТИПИ СТЕПІНЬ ЧИСЛА РОЗДІЛ 4 СТЕПІНЬ НАТУРАЛЬНОГО ЧИСЛА З НАТУРАЛЬНИМ ПОКАЗНИКОМ. ПЛОЩІ ТА ОБ’ЄМИ ФІГУР У розділі дізнаєтесь: Що таке степінь числа і як він пов’язаний із дією множення; Про дію піднесення до степеня та її властивості; Що таке квадрат і куб числа; Який порядок виконання дій у виразах, що містять степені; Що таке многокутник та які його […]...

  18. Степінь з цілим від’ємним показником Тестові завдання Тестове завдання № 3 . Степінь з цілим від’ємним показником 1. При якому t правильна рівність ? А Б В Г -2 5 -5 -3 2. Знайдіть значення виразу . А Б В Г 1 3. Перетворіть у дріб: ху -1 + ху -2. А Б В Г 4. Обчисліть: 104 : (0,01) […]...

  19. Степінь Математика – Алгебра Подільність натуральних чисел Степінь Добуток n однакових множників, кожний із яких дорівнює а, називається n-м Степенем числа А і записується : , де n – натуральне число. Вираз називається степенем, число a – основою степеня, число n – показником сте­пеня. Приклади ; ....

  20. ВЛАСТИВОСТІ СТЕПЕНЯ З НАТУРАЛЬНИМ ПОКАЗНИКОМ Цілі: – навчальна: удосконалити вміння застосовувати властивості степенів до розв’язування задач; – розвивальна: формувати вміння міркувати за аналогією; розвивати увагу, логічне мислення, пам’ять; – виховна: виховувати об’єктивність та чесність під час оцінювання власних знань, старанність, наполегливість у досягненні мети; Тип уроку : удосконалення вмінь і навичок. Обладнання та наочність: Хід уроку І. ОРГАНІЗАЦІЙНИЙ ЕТАП ______________________________________________________ […]...

Ви зараз читаєте: Степінь з раціональним показником – СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ
«
»