Головна ⇒ 📌ГДЗ з математики ⇒ Суміжні та вертикальні кути

Суміжні та вертикальні кути

§ 1. Найпростіші геометричні фігури та їхні властивості

§ 4. Суміжні та вертикальні кути

Практичні завдання

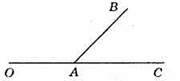
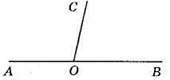
86. ∠BAC – гострий, ∠OAB – суміжний до кута ВАС.

Суміжні та вертикальні кути

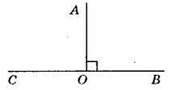
∠АОВ – прямий, ∠COA – суміжний до кута АОВ.

Суміжні та вертикальні кути

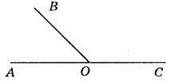
∠BOC – тупий, ∠AOB – суміжний до кута ВОС.

Суміжні та вертикальні кути

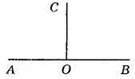
87. ∠AOC і ∠COB – суміжні.

Суміжні та вертикальні кути

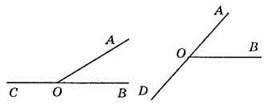
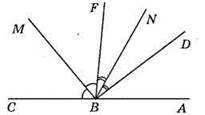
88. а) ∠ABD i ∠CBD;

Б) ∠MKP i ∠PKO; ∠MКЕ і ∠ERO;

В) ∠FCN і ∠NCE; ∠FCM і ∠MCE;

Г) ∠ABC і ∠CBD; ∠ADF і ∠FDE.

89. а) Ні;

б) так; в) ні.

90. ∠AOC i ∠COB; ∠COB і ∠BOD; ∠BOD і ∠DOA; ∠DOA і ∠AOC – суміжні.

∠AOC і ∠BOD; ∠AOD і ∠BOC – вертикальні.

91. 1) 24°+ 156°= 180°. Можуть.

2) 63° + 107° = 170° ≠ 180°. Не можуть.

Відповідь: 1) так; 2) ні.

92. 1) 180° – 29° = 151°; 2) 180° – 84° = 9G°; 3) 180° – 98° = 82°; 4) 180° – 135° = 45°.

Відповідь: 1) 151°; 2) 96°; 3) 82°; 4) 45°.

93. 1) Два гострих кута не можуть бути суміжними, бо їх сума менша 180°.

2) Два тупих кути не можуть бути суміжними, бо їх сума більша 180°.

3) Прямий і тупий кути не можуть бути суміжними, бо їх сума більша 180°.

4) Прямий і гострий кути не можуть бути суміжними,

бо їх сума менша 180°.

Відповідь: 1) ні; 2) ні; 3) ні; 4) ні.

94. Якщо один із суміжних кутів прямий, то суміжний з ним кут теж прямий.

Відповідь: прямий.

95. 1) 180° – ∠ABC= 180° -36° =144°.

2) 180° – ∠ABC = 180° – 102° = 78°.

Відповідь: 1) 144°; 2) 78°.

96. ∠2 = 180° – ∠1 = 180° – 42° = 138° (бо ∠1 і ∠2 – суміжні); ∠3 = ∠1 = 42° (бо ∠1 і ∠3 – вертикальні); ∠4 = ∠2 = 138° (бо ∠4 і ∠2 – вертикальні).

Відповідь: ∠2 = 138°; ∠3 = 42°; ∠4 = 138°.

97. 1) Нехай ∠BOC = х°, тоді ∠AOC = х° + 70°. Оскільки ∠AOC + ∠COB = 180°, маємо рівняння: х + 70 + х = 180, звідси 2х + 70 = 180; 2х = 180 – 70; 2х = 110; х = 110 : 2; х = 55, тоді х + 70 = 55 + 70 = 125. Отже, ∠BOC = 55°, ∠AOC = 125°.

Суміжні та вертикальні кути

Відповідь: 125° і 55°.

2) Нехай ∠BOC = х°, тоді ∠AOC = 8х°. Оскільки ∠AOC + ∠COB = 180°, то маємо рівняння: 8х + х = 180, звідси 9х = 180; х = 180 : 9; х = 20, тоді 8х = 8 х 20 = 160. Отже, ∠BOC = 20°, ∠AOC = 160°.

Відповідь: 20° і 160°.

Суміжні та вертикальні кути

3. Нехай ∠BOC = 2х°, тоді ∠AOC = 3х°. Оскільки ∠AOC + ∠COB = 180°, то маємо рівняння, 2х + 3х = 180, звідси 5х = 180; х = 180 : 5; х = 36, тоді 2х = 2 х 36 = 72°, 3х = 3 х 36 = 108. Отже,∠BOC = 72°, ∠AOC = 108°.

Б) Неправильне твердження, бо вони можуть прямими.

Суміжні та вертикальні кути

Відповідь: 72° і 108°.

98. 1) Нехай ∠BOC = х°, тоді ∠AOC = 17х°. Оскільки ∠AOC + ∠BOC = 180°, то маємо рівняння: х + 17х = 180, звідси 18х =180; х =180 : 18; х = 10, тоді 17х = 17 х 10 = 170. Отже, ∠BOC = 10°,∠AOC =170°.

Суміжні та вертикальні кути

Відповідь: 10° і 170°.

2) Нехай ∠BOC = 19*°, тоді ∠AOC = 26*°. Оскільки ∠AOC + ∠BOC = 180°, то маємо рівняння 19х + 26х = 180, звідси 45х = 180; х = 180 : 45; х = 4, тоді 19х = 19 х 4 = 76, 26х = 26 x 4 = 104. Отже, ∠BOC = 76°, ∠AOC = 104°.

Суміжні та вертикальні кути

Відповідь: 76° і 104°.

99. 1) Правильне твердження.

2) Неправильне твердження, бо для кожного кута, відмінного від розгорнутого, можна побудувати два суміжних кути.

Суміжні та вертикальні кути

3) Неправильне, бо якщо кути рівні, то вони не є обов’язково вертикальними.

Суміжні та вертикальні кути

4) Правильне твердження.

5) Неправильне твердження.

Б) Неправильне твердження, бо вони можуть прямими.

Суміжні та вертикальні кути

7) Неправильне твердження, бо вони можуть бути рівними.

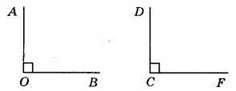
8) Неправильне твердження, бо сума кутів АОВ і DCF дорівнює 180°, проте вони не є суміжними.

Суміжні та вертикальні кути

9) Правильне твердження.

10) Правильне твердження.

11) Правильне твердження.

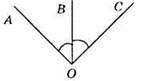
12) Неправильне твердження, бо ∠AOB = ∠BOC, проте ∠AOB і ∠BOC – не є вертикальними.

Суміжні та вертикальні кути

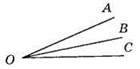
13) Неправильне твердження, бо кути АОС і ВОС мають спільну сторону ОС, проте вони не є суміжними.

Суміжні та вертикальні кути

100. Два кути, утворені при перетині двох прямих, можуть бути або суміжними, або вертикальними. Якщо б вони були суміжними, то їх сума дорівнювала б 180°, але це не так. Тому ці кути є вертикальними.

101. 1) Нехай ∠1 + ∠2 = 106°. Оскільки ∠1 і ∠2 – вертикальні, то ∠1 = ∠2 = 106° : 2 = 53°. Оскільки ∠2 і ∠3 – суміжні, то ∠3 = 180° – ∠1 = 180° – 53° = 127°. Оскільки ∠3 i ∠4 – вертикальні, то∠4 = ∠3 = 127°.

Суміжні та вертикальні кути

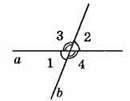
Відповідь: 53°, 127°, 53°, 127°.

2) Нехай ∠4 + ∠2 + ∠3 = 305°. Оскільки ∠2 і ∠4 – суміжні, то ∠4 + ∠2 = 180°, тоді ∠3 = 305° – 180° = 125°. Оскільки ∠3 і ∠4 – вертикальні, то ∠4 = ∠3 = 125°. Оскільки ∠2 і ∠4 – суміжні, то ∠2= 180° – 125° = 55°. Оскільки ∠1 і ∠2 – вертикальні, то ∠1 = ∠2 = 55°.

Відповідь: 55°, 125°, 55°, 125°.

102. Нехай ∠3 – ∠2 = 64°, Z2 = х°, тоді ∠3 = х° + 64°. Враховуючи, що ∠2 i ∠3 – суміжні, то х + х + 64 = 180. Звідси 2х + 64 = 180; 2х = 116; х = 116 : 2; х = 58, тоді х + 64 = 58 + 64 = 122. Отже ∠2 = 58°, Z3 = 122°. Оскільки ∠1 і ∠2, ∠3 і ∠4 – вертикальні, то ∠1 = ∠2 = 58°, ∠4 = ∠3 = 122°.

Відповідь: 58°, 122°, 58°, 122°.

103. ∠1 і ∠4, ∠3 і ∠5 – вертикальні, тоді ∠4 = ∠1, ∠3 = ∠5.

∠1 + ∠2 + ∠3 = ∠4 + ∠2 + ∠5 = 180°.

Суміжні та вертикальні кути

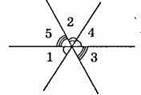
Відповідь: 180°.

104. ∠MOC = 180° – ∠BOM – ∠AOC = 180° – 70° – 15° = 95°.

∠DOK і ∠COM – вертикальні, то ∠DOK = MOC = 95°.

∠AOM = ∠AOC + ∠COM = 70°+ 95° = 165°.

∠АОD = ∠АОK + ∠КOD = 15° + 95° = 110°.

Відповідь: 95°, 165°, 110°.

105. ∠AOC i ∠BOC – суміжні, OM i ON – бісектриси кутів AOC і BOC відповідно.

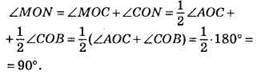
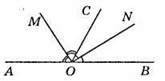
Суміжні та вертикальні кути

Суміжні та вертикальні кути

Відповідь: 90°.

106. ∠AOC і ∠DOB – вертикальні, ОМ і ON – бісектриси кутів АОС і BOD. ∠MON = ∠1 + ∠AOD + ∠3 = ∠1 + ∠2 + ∠BOC = ∠AOC + ∠BOC = 180°.

Суміжні та вертикальні кути

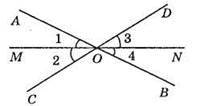
Відповідь: 180°.

107. ∠ABF = 80°, ∠ABD = 30°, BM і BN – бісектриси кутів FBC і FBD.

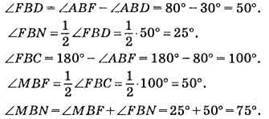
Суміжні та вертикальні кути

Суміжні та вертикальні кути

Відповідь: 75°.

108. ∠AOB i ∠BOC – суміжні, BD – бісектриса кута АОВ, ∠BOC – ∠BOD = 18°. Нехай ∠BOD = х°, тоді ∠AOD = х°, ∠BOC = х° + 18°. Враховуючи, що ∠AOD + ∠DOB + ∠BOC = 180°, маємо рівняння: х + х + х + 18 = 180, звідси 3х + 18 = 180; 3х = 180 – 18; 3х = 162; х = 162 : 3; х = 54. Тоді ∠AOB = 2 х 54° = 108°, ∠BOC = 54° + 18° = 72°.

Суміжні та вертикальні кути

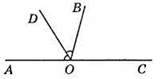
Відповідь: 72° і 108°.

109. Кути МКЕ і РКЕ – суміжні. KF – бісектриса кута МКЕ, ∠FKE – ∠PKE = 24°. Нехай ∠PKE = х°, тоді ∠MKF = ∠FKE = х° + 24°. Враховуючи, що ∠MKF + ∠FKE + ∠EKP = 180°, маємо рівняння: х + 24 + х + 24 + х = 180, звідси 3х + 48 = 180; 3х = 180 – 48; 3х = 132; х = 132 : 3; x = 44. Toдi ∠PKE = 44°, ∠MKE = 180° – 44° = 136°.

Суміжні та вертикальні кути

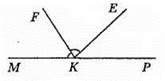
Відповідь: 136° і 44°.

110. Нехай ∠ACB = х°, тоді з умови ∠MAB + ∠ACB = 180° випливає, що ∠MAB = 180° – ∠ACB = 180° – х°. Оскільки ∠ACB і ∠KCB – суміжні, то ∠KCB = 180° – ∠ACB = 180° – х°. Отже, ∠MAB =∠KCB = 180° – х°.

111. Якщо ∠MBC = ∠BEF, тоді ∠ABE + ∠BED = ∠MBC + (180° – ∠BEF) = ∠MBC + (180° – ∠MBC) = ∠MBC + 180° – ∠MBC = 180°.

112. Якщо два кути мають спільну сторону і їхня сума дорівнює 180°, то не обов’язково ці кути будуть суміжними. ∠AOB і ∠BOC мають спільну сторону OB і ∠AOB + ∠BOC = 120° + 60° = 180°, проте ∠AOB і ∠BOC не є суміжними.

Суміжні та вертикальні кути

Спостерігайте, рисуйте, конструюйте, фантазуйте

113. Прямі а і b розбивають фігуру на шість частин.

Суміжні та вертикальні кути


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Суміжні й вертикальні кути Геометрія Основні властивості найпростіших геометричних фігур Суміжні й вертикальні кути Два кути називаються Суміжними, якщо в них одна сторона спільна, а інші сторони є доповняльними півпрямими. На рисунку і – суміжні. Властивості суміжних кутів Теорема 1. Сума суміжних кутів дорівнює . (Зверніть увагу: кути, сума яких дорівнює , не обов’язково суміжні.) Теорема 2. Коли два […]...

  2. СУМІЖНІ І ВЕРТИКАЛЬНІ КУТИ Геометрія Евкліда є лише першим кроком до вивчення форм реального простору. О. Смогоржевський РОЗДІЛ 2 ВЗАЄМНЕ РОЗТАШУВАННЯ ПРЯМИХ НА ПЛОЩИНІ У цьому розділі підручника ви розширите і поглибите свої знання про прямі і промені однієї площини, ознайомитеся з дуже важливими поняттями: суміжні кути, вертикальні кути, перпендикулярні прямі, паралельні прямі тощо, а також із важливими загальноматематичними […]...

  3. Вертикальні кути. Кут між двома прямими, що перетинаються Розділ 2. Взаємне розміщення прямих па площині § 6. Вертикальні кути. Кут між двома прямими, що перетинаються 107. 1) За властивістю вертикальних кутів – вертикальні кути рівні. Отже, кут, вертикальний до кута 15°, дорівнює 15°. 2) За властивістю вертикальних кутів – вертикальні кути рівні. Отже, кут, вертикальний до кута 129°, дорівнює 129°. Відповідь: 1) 15°; […]...

  4. Вертикальні кути Розділ 1. Найпростіші геометричні фігури та їх властивості § 5. Вертикальні кути 152. 1) ∠AYX і ∠BYZ – вертикальні; 2) ∠OLK і ∠MLN – не вертикальні. 153. 1) ∠AOD – вертикальний з кутом 1; 2) ∠АОС і ∠DOB – суміжні з кутом 1. 154. ∠BOA і ∠COD – суміжні. ∠BOA = ∠COD = 60°. 155. […]...

  5. Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих Розділ 2. Взаємне розміщення прямих па площині § 9. Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих 170. Рис. 119: ∠1 і ∠2 – внутрішні різносторонні кути. Рис. 120: ∠1 і ∠2 – відповідні кути. Рис,121: ∠1 i ∠2 – внутрішні різносторонні кути. 171. Внутрішні односторонні кути: ∠ANM і ∠NMB, ∠CNM і ∠NMD. […]...

  6. Суміжні кути Урок № 10 Тема. Суміжні кути Мета: домогтися розуміння учнями змісту наслідків з теореми про суму суміжних кутів та змісту понять “наслідок”, “посилання”; використовуючи знання теореми про суміжні кути та її наслідки, виробити вміння розв’язувати задачі на обчислення та доведення, в яких йдеться про суміжні кути. Тип уроку: застосування знань, умінь та навичок. Наочність і […]...

  7. Вертикальні кути. Кут між прямими Урок № 11 Тема. Вертикальні кути. Кут між прямими Мета: домогтися засвоєння учнями означення вертикальних кутів, формулювання і доведення теореми про властивість вертикальних кутів; означення кутів між прямими. Сформувати вміння: – будувати вертикальні кути; – знаходити вертикальні кути на рисунку; – розв’язувати задачі із застосуванням теореми про рівність вертикальних кутів та суму суміжних кутів. Тип […]...

  8. Вправи для повторення до розділу 2 Розділ 2. Взаємне розміщення прямих па площині Вправи для повторення до розділу 2 До § 5. 226. На рис. 184 суміжні кути ∠2 і ∠3. на рис. 185 суміжні кути ∠1 і ∠4 та ∠2 i ∠3. На рис. 186 суміжні кути ∠1 і ∠2 та ∠3 i ∠4. 227. 1) Так, можна. Треба побудувати […]...

  9. Вправи 150-175 150. ∠1 = 90°, ∠2 = ∠1 = 90° – вертикальні кути; ∠3 – суміжний куту ∠1. ∠3 = 180° – 90° = 90°, ∠3 = ∠4 = 90° (вертикальні кути). 151. ∠(ac) = 70°; ∠(ab) = 90°; ∠(bc) = 90° – ∠(ac) = 90° – 70° = 20°. 152. а ⊥ с; ∠(ab) = […]...

  10. Вправи 100-49 100. А || b, с || d. 4 точки перетину. 101. 1) Всі чотири прямі перетинають пряму с. 2) Одна пряма паралельна, три перетинають пряму с. 102. 1) m || с; 2) m || b; в) m || а. 103. а || b. Якщо b i c не перетинаються, то через т. М проведено 2 […]...

  11. Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною Розділ 2. Взаємне розміщення прямих па площині § 10. Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною 199. 1) ∠1 = ∠8, ∠6 = ∠3 (як відповідні кути при паралельних прямих а і b і січній с). 2) ∠2 = ∠4 (як внутрішні різносторонні кути при паралельних прямих а і b і […]...

  12. Вправи 375-424 375. ВС – бісектриса ∠ABD; ∠ABD = 80° + 80° = 160°; ∠BAC + ∠ABD = 20° + 160° = 180°; ∠BAC і ∠ABD – внутрішні односторонні кути при прямих АС і BD та січній АВ. Отже, BD || АС. 376. ∠A = 70°, ∠B = 40°, BE – бісектриса ∠ABD; ∠DBE = ∠ABE = […]...

  13. Многогранні кути 607. Правильний октаедр має 8 граней, кожна з яких – правильний трикутник. Він має 6 чотиригранних кутів. 608. Чотиригранний кут 40°; 70°; 110° і 140° існує неопуклий. 609. Якщо всі плоскі кути чотиригранного кута рівні, то кожний його двогранний кут дорівнює протилежному (октаедр). Площини, які проходять через його протилежні ребра, – перпендикулярні. 611. Якщо у […]...

  14. Зовнішній кут трикутника та його властивості Розділ 3. Трикутники. Ознаки рівності трикутників § 18. Зовнішній кут трикутника та його властивості 438. ∠BAK – зовнішній кут при вершині А. 439. ∠LDP – зовнішній кут при вершині D. 441. ∠A + ∠B = 70° – за властивістю зовнішнього кута трикутника. 442. Зовнішній кут трикутника при вершині С дорівнює 74° згідно з властивістю зовнішнього […]...

  15. Рівнобедрений трикутник і його властивості § 2. Трикутники 8. Рівнобедрений трикутник і його властивості Практичні завдання 196. 197. 198. Вправи 199. 1) Р = 13 + 2 х 8 = 29(см). Відповідь: 29 см. 2) Нехай х см – бічна сторона, тоді 15 + 2х = 39, тоді 2х = 39 – 15; 2х = 24; х = 24 : […]...

  16. Кути – ПЛАНІМЕТРІЯ Формули й таблиці МАТЕМАТИКА ПЛАНІМЕТРІЯ Паралельні прямі перетинають сторони кута. Кути Кут – плоска фігура, що складається із двох променів зі цільним початком й обмеженої ними частини площини. Промені називаються сторонами, їхня спільна точка – вершиною, обмежена ними частина площини – внутрішньою областю. α + α’ = 180° α і α’ – суміжні кути β […]...

  17. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 19. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників 466. 1) PF – гіпотенуза, PL і LF – катети. 2) PF довша за PL, PF довша за LF, оскільки PF – гіпотенуза. 467. На рис. 321 трикутники рівні за двома катетами. Оскільки АС = ML, СВ = LP, […]...

  18. Коло і його елементи Розділ 4. Коло і круг. Геометричні побудови § 21. Коло і його елементи 578. PL – хорда, що проходить через центр кола, називається діаметром. 579. 1) 5 х 2 = 10(см); 2) 4,7 х 2 = 9,4 (дм). 580. 1) 8 мм х 2 = 16 мм; 2) 4,8 см х 2 = 7,6 см. […]...

  19. Тригранні кути 562. Нехай дано тригранний кут, усі плоскі кути якого прямі. Лінійний кут кожного тригранного кута прямий, отже всі його двогранні кути прямі. 563. Якщо всі двогранні кути тригранного кута рівні, то кожний з них більше за 60°, оскільки ∠1 + ∠2 + ∠3 > 180°; ∠Α = ∠1 – ∠2 = ∠3, то 3∠A > […]...

  20. Вправи 275-324 275. Кут В. а) ВА = ВС, ?АВС – рівнобедрений, у нього дві сторони рівні; Б) ∠A = ∠C. 276. ∠A = 60°; AD – бісектриса кута А. BC ⊥ AD; AB = AC; ∠B = ∠C. 277. AB = ВС; АС – основа. Нехай АВ = ВС = х м, тоді АС = (х […]...

  21. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника Розділ 3. Трикутники. Ознаки рівності трикутників § 15. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника 351. 1) AT – висота трикутника ABC. 2) AN – медіана трикутника ABC. 3) АР – бісектриса трикутника? AВС. 352. Оскільки AK – висота, то ∠BKA = ∠CKA = 90°. 353. Оскільки АК – бісектриса, то ∠BAK = […]...

  22. Перша та друга ознаки рівності трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 13. Перша та друга ознаки рівності трикутників 301. На рис. 227 трикутники рівні за першою ознакою (за двома сторонами і кутом між ними). На рис. 228 трикутники рівні за другою ознакою (за стороною і прилеглими двома кутами). 302. У? ABC і? CDA спільний елемент – сторона AВ. У? […]...

  23. Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої Розділ 2. Взаємне розміщення прямих па площині § 7. Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої 128. m ⊥ n, MN ⊥ АВ. 129. KA ⊥ c, ВМ ⊥ с. 130. ВL ⊥ a. MВ ⊥ a. 131. 1) Відрізки AB і MN перпендикулярні, оскільки вони лежать на перпендикулярних прямих a і b. 2) […]...

  24. Ознаки паралельності двох прямих § 3. Паралельні прямі. Сума кутів трикутника 13. Ознаки паралельності двох прямих Практичні завдання 300. 1) Кути АОМ і CEO – відповідні; 2) кути АОЕ і СЕК – відповідні; 3) кути АОE і OED – різносторонні; 4) кути АОЕ і CEO – односторонні. 1) відповідні; 2) односторонні; 3) різносторонні. 301. 1) ∠1 i ∠5; ∠2 […]...

  25. Властивості й ознака рівнобедреного трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 12. Властивості й ознака рівнобедреного трикутника 476. На мал. 72: ML і МК – бічні сторони, KL – основа, ∠K = ∠L. 477. KD = DF, КЕ = EF, ∠K = ∠F, ∠KDE = ∠FDE, ∠DEK = ∠DEF = 90°. 478. Щоб провести бісектрису, медіану і […]...

  26. Рівність геометричних фігур Розділ 1. Найпростіші геометричні фігури та їх властивості § 11. Рівність геометричних фігур 397. Щоб сумістити фігури F1 i F, можна скопіювати фігуру F1 на кальку, потім перевернути кальку і покласти на фігуру F. 398. Відрізки OP і MN сумістити не можна, бо вони мають різну довжину. 399. Кути ABC і MON сумістити не можна, […]...

  27. Кути трикутника і чотирикутника. Розв’язання задач Урок № 51 Тема. Кути трикутника і чотирикутника. Розв’язання задач Мета. Продовжити формування в учнів. вміння розв’язувати задачі геометричного змісту, повторити основні поняття теми, сприяти формуванню практичних навичок при виконанні вправ. Форми роботи: фронтальна бесіда, індивідуальна робота біля дошки, виконання тренувальних вправ, робота з підручником. Обладнання: лінійка, транспортир, кольорова крейда, косинець, таблиці. Тип уроку: урок […]...

  28. Двогранні кути 520. Нехай дано двогранний кут, міра якого 60°, ∠AOB = 60°. AO + MN, BO + MN, АВ + β, АВ = 12 см. ΔАОВ – прямокутний. 521. Нехай дано двогранний кут, який дорівнює 45°. т. В? α, ОВ = 8 дм. АВ + β. Δ ΟΒΑ – прямокутний. 522. Нехай дано двогранний кут ∠BOA. […]...

  29. Теореми § 2. Трикутники 11. Теореми 269. Теорема Умова Висновок 4.1 Кути АОС і СОВ – суміжні ∠AOC + ∠COB = 180° 8.2 X належить серединному перпендикуляру відрізка AB ХА = ХВ 9.1 ?ABC – рівнобедрений з основою АС 1) ∠A = ∠C; 2) бісектриса кута В є медіаною і висотою 10.3 Два кути трикутника ABC […]...

  30. Кут. Вимірювання кутів. Бісектриса кута Розділ 1. Елементарні геометричні фігури та їхні властивості § 3. Кут. Вимірювання кутів. Бісектриса кута 33. 1) М – вершина кута, МА і МК – сторони кута АМК; 2) L – вершина кута, LP і LF – сторони кута PLF; 3) N – вершина кута, NB i NC – сторони кута BNC. 34. 1) O […]...

  31. Властивості прямокутного трикутника § 3. Паралельні прямі. Сума кутів трикутника § 17. Властивості прямокутного трикутника 457. Найбільший катет трикутника дорівнює 24 см. 458. ?DEF – прямокутний, ∠F = 90°, ∠D = 30°, DE = 18 см. Відповідь: 9 см. 459. ?KCM – прямокутний, ∠M = 90°, ∠C = 60°, MC = 7 см. ∠MKC = 90° – 60° […]...

  32. Ознаки рівнобедреного трикутника § 2. Трикутники 9. Ознаки рівнобедреного трикутника 232. ?ABC – рівнобедрений, тому ВК є бісектрисою кута ABC, отже, ∠ABC = 2 х ∠ABK = 2 x 25° = 50°. Відповідь: 50°. 233. BK є висотою та медіаною, тому? ABC – рівнобедрений, AB = ВС, отже, ∠C = ∠A =17°. Відповідь: 17°. 234. AС = ВС, […]...

  33. Ознаки рівності прямокутних трикутників Розділ 1. Найпростіші геометричні фігури та їх властивості § 14. Ознаки рівності прямокутних трикутників 549. Ні, трикутники не рівні. 550. Мал. 319. ?САВ = ?HDQ (за катетом і гострим кутом: CA = HD, ∠C = ∠H). Мал. 320. ?ABC = ?CDA (за гіпотенузою АС і гострим кутом: ∠BAC = ∠DAC). Мал. 321. ?АОВ = ?DCО […]...

  34. Вправи 325-374 325. ?ABC; AB = AC; ?A1B1C1; A1B1 = A1C1; ∠B = ∠B1; BK = B1K1. ∠AKB = ∠CKB = ∠A1K1B1 = ∠C1K1B1 = 90°. ?АВK = ?A1B1K1. 1) BK = В1K1; 2) ∠1 = ∠2; 3) ∠3 = ∠4, отже, AB =A1B1. ?АВС = ?А1В1С1. AB = A1B1; BC = В1С1; ∠B = ∠B1. 326. […]...

  35. Тригранний і многогранний кути Геометрія Многогранники Тригранний і многогранний кути Нехай промені a, b, c виходять з однієї точки й не лежать в одній площині. Тригранним кутом називається фігура, яка складається з трьох плоских кутів , , (див. рисунок). Ці кути називаються Гранями тригранного кута, а їх сторони – Ребрами. Спільна вершина плоских кутів називається Вершиною тригранного кута. Двогранні […]...

  36. Промінь. Кут. Вимірювання кутів § 1. Найпростіші геометричні фігури та їхні властивості 3. Промінь. Кут. Вимірювання кутів Практичні завдання 49. Промені AB і АС – не доповняльні. Промінь AN – доповняльний до променя AB, а промінь AM – доповняльний до променя АС. На рисунку зображено промені АB, АС, AN, AM. 50. Промені AB і ВА не е доповняльними, оскільки […]...

  37. Рівні трикутники. Висота, медіана, бісектриса трикутника § 2. Трикутники 6. Рівні трикутники. Висота, медіана, бісектриса трикутника Практичні завдання 132. 133. ВН – спільна висота трикутників ABD, ABC, BDC. ВН лежить поза трикутником BCD. 134. 135. 136. Вправи 137. 1) ME; 2) ∠E; 3) MK i KE; 4) ∠K i ∠E. 138. 1) ∠E; 2) ∠C i ∠E;3) CF; 4) CF і […]...

  38. Властивості кутів трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 10. Властивості кутів трикутника 344. ∠E = 60°, ∠F = 40°, ∠D = 80°. ∠E + ∠F + ∠D = 60° + 40° + 80° = 180°. 345. На мал. 208 неправильно сказано градусну міру кутів? АВС, оскільки? ABC – прямокутний, a ∠B + ∠C = […]...

  39. Кути трикутника і чотирикутника Урок № 50 Тема: Кути трикутника і чотирикутника Мета. Познайомити учнів з видами кутів і трикутників в залежності від кутів, які входять до кута. Навчити учнів вимірювати кути за допомогою транспортира. Формувати уміння і навички розв’язувати геометричні задачі. Розвивати логічне мислення учнів, шляхом розв’язування задач, продовжувати формувати вміння працювати з підручником. Форми роботи: бліцопитування, робота […]...

  40. Вправи 475-524 475. ?ABC – прямокутний; ∠A = 30°; АС = 18 см; ВК – бісектриса, проведена до катета АС; ∠CBK = ∠ABK = ∠CBA : 2 = 60° : 2 = 30°; ∠CBA = 90° – ∠CAB = 90° – 30° = 60°; СК = х, тоді AK = 18 – х. ?АВК – прямокутний; ∠A […]...

Ви зараз читаєте: Суміжні та вертикальні кути
«
»