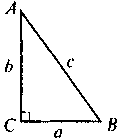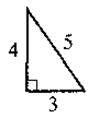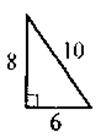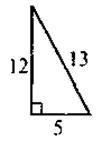Теорема Піфагора
Урок № 34
Тема. Теорема Піфагора
Мета: сформувати в учнів розуміння змісту теореми Піфагора та її доведення. Формувати вміння відтворювати зміст теореми Піфагора, застосовувати її формулювання для розв’язування задач на знаходження невідомих сторін прямокутних трикутників.
Типу уроку: засвоєння нових знань.
Наочність та обладнання: конспект “Теорема Піфагора”.
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Під час усного обговорення контрольних моментів розв’язання домашніх задач
Обговорення розв’язування задачі 4 сприяє повторенню опорного факту: медіана прямокутного трикутника, що проведена до гіпотенузи, ділить:
– даний трикутник на два рівнобедрених трикутники, основами яких є катети даного трикутника;
– прямий кут прямокутного трикутника на два купи, що дорівнюють гострим кутам даного прямокутного трикутника.
III. Формулювання мети і завдань уроку
Для усвідомлення учнями важливості матеріалу,
Задача. Чи можна прямокутник зі сторонами 6 см і 8 см вписати в коло з радіусом 5 см?
Щоб знайти відповідь на запитання задачі, учні мають скласти математичну модель задачі, яка має такий вигляд: знайти діагональ прямокутника зі сторонами 6 см і 8 см або знайти гіпотенузу прямокутного трикутника з катетами 6 см і 8 см. Аналіз ситуації приводить учнів до усвідомлення неможливості (або нераціональності) розв’язання задачі засобами, якими оволоділи учні на попередніх етапах вивчення геометрії. Таким чином, констатується необхідність розширення знань учнів щодо співвідношень в прямокутному трикутнику. Тому завдання на урок формулюється так: спираючись на відомі учням співвідношення в прямокутному трикутнику, сформулювати твердження, що виражає залежність між сторонами прямокутного трикутника, довести його. А також сформувати вміння застосовувати ці залежності для знаходження невідомих сторін прямокутного трикутника.
IV. Актуалізація опорних знань
З метою успішного засвоєння учнями змісту теореми Піфагора та її доведення учням слід активізувати знання і вміння щодо означення прямокутного трикутника; метричних співвідношень у прямокутному трикутнику.
Виконання усних вправ за готовими рисунками
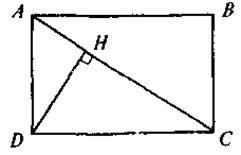
1 |
|
1) АС2, СН, якщо АН = 2, ВН = 8; 2) АН, якщо ВС = 6, НВ = 4; 3) СН, якщо АС = 3, ВС = 4; 4) АВ, якщо ВС = 10, СН = 6 |
2 |
| DH 1) РАBCD, якщо АН = 9, СН = 16; 2) DH, якщо АВ = 12, AD = 5; 3) АС, якщо AD = 15, DH = 12; 4) РABCD, якщо AD + DC = 70, AH – HC = 9 – 16 |
V. Засвоєння знань
План вивчення нового матеріалу
1. Теорема Піфагора: доведення та формулювання.
2. Приклади застосування.
@ На відміну від попередніх років, коли доведення теореми Піфагора здійснювалось із посиланням на властивості косинуса гострого кута прямокутного трикутника, в новому підручнику теорема Піфагора дуже просто доводиться із посиланням на метричні співвідношення в прямокутнику трикутнику. Тому доведення теореми Піфагора можна провести в такому порядку:
– розглянути прямокутний трикутник з катетами а і b, гіпотенузою с і висотою, проведеною до гіпотенузи hc;
– для нього трикутника записати метричні співвідношення для катетів;
– виконати почленне додавання обох частин здобутих рівностей;
– перетворити праву частину здобутої рівності, використавши аксіому вимірювання відрізків.
Після здобуття шуканої рівності вчитель пропонує учням “перекласти” її з математичної мови на звичайну. Таким чином учні формулюють твердження теореми Піфагора.
На завершення вивчення матеріалу як приклад на застосування теореми учні розв’язують задачу, з якої почалося вивчення матеріалу на уроці: знайти гіпотенузу, якщо катети дорівнюють 6 см і 8 см (c2 = 62 + 82 = 100, с = 10). Таким чином демонструється практичне значення вивченої теореми.
Наостанок можна підкреслити, що з теореми Піфагора випливає властивість, вивчена у 7 класі: гіпотенуза даного прямокутного трикутника завжди більша за його катет.
Під час розгляду прикладів розв’язання задач на застосування теореми Піфагора за підручником слід перевірити відповідність знань учнів щодо змісту поняття квадратний корінь. Так само у відборі задач до уроку слід пам’ятати про необхідність дотримання відповідності між геометричним та алгебраїчним матеріалом.
Конспект 13 |
|
Теорема Піфагора. Обернена теорема до теореми Піфагора Теорема Піфагора. Якщо в? ВС | |
Обернена теорема. Якщо в? АВС АВ2 = АС2 + ВС2, то | |
Піфагорові трійки чисел Якщо числа а, b, с такі, що а2 + b2 = с2, то трійка чисел а, b, с – піфагорова трійка, а трикутники зі сторонами а, b, с – піфагорові. | |
|
|
Єгипетський трикутник | Піфагорові трикутники |
VI. Формування первинних умінь
Виконання усних вправ
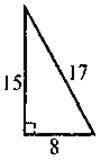
1. Для яких трикутників, зображених нарис. 1, виконується теорема Піфагора? Виконайте відповідні записи.
Рис. 1
2. “Мені вдалося побудувати прямокутний трикутник, у якого довжини всіх сторін – цілі непарні числа”, – сказав учень. Доведіть, використовуючи теорему Піфагора, що він помилився.
3. У ромбі відомі сторона та одна з діагоналей. Як знайти іншу діагональ ромба, не користуючись рисунком?
4. 1) Катети прямокутного трикутника 5 см і 12 см. Знайдіть гіпотенузу.
2) Гіпотенуза трикутника 5 см, а один із катетів дорівнює 3 см.
Знайдіть другий катет.
3) Катети прямокутного трикутника відносяться як 3 . 4, а гіпотенуза дорівнює 15 см. Знайдіть периметр трикутника.
4) Периметр квадрата дорівнює 4 см. Знайдіть діагональ квадрата.
5) Визначте вид трикутника ABC, якщо: 1) АС = 5, ВС = 6 , АС = 7; 2) АС = 4. ВС = 2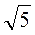 , AC = 6.
, AC = 6.
Виконання графічних вправ
Накресліть прямокутний трикутник із катетами 3 см і 4 см. Обчисліть за теоремою Піфагора довжину його гіпотенузи. Перевірте результат вимірюванням.
Виконання письмових вправ
1. У прямокутному трикутнику з катетами а і b та гіпотенузою с знайдіть с, якщо а = 7, b = 24 .
2. У прямокутнику знайдіть периметр, якщо діагональ дорівнює 10 см, а одна зі сторін – 6 см.
3. Основа рівнобедреного трикутника дорівнює 16 см. Знайдіть периметр трикутника, якщо його бісектриса, проведена до основи, дорівнює 6 см.
4. У прямокутному трикутнику знайдіть невідомі сторони, якщо:
А) катети відносяться як 3 : 4. а гіпотенуза дорівнює 45 см;
Б) різниця між гіпотенузою і катетом дорівнює 1 см, а другий катет дорівнює 5 см;
В) висота, проведена до гіпотенузи, дорівнює 12 см, а проекція одного з катетів на гіпотенузу має довжину 16 см.
5. Основи рівнобедреної трапеції дорівнюють 8 см і 18 см, а висота 12 см. Знайдіть периметр трапеції. Чи можна вписати в неї коло?
6. Дві більші сторони прямокутного трикутника дорівнюють 65 см і 63 см. Знайдіть третю сторону.
Оскільки на уроці розпочинається робота із формування вмінь застосовувати теорему Піфагора, то слід одразу виробляти в учнів навички математичної культури, тобто застосуванню теореми Піфагора для деякого прямокутного трикутника мають передувати такі міркування:
Розглянемо трикутник…, у ньому кут… – прямий, отже, трикутник прямокутний із гіпотенузою… Тому за теоремою Піфагора… (робиться загальний запис теореми для даного прямокутного трикутника).
Тільки після цього можливе виконання обчислень, складання рівняння, вираження невідомих тощо. (Згодом ці міркування можна буде скорочувати, але на першому уроці цього робити не слід).
VII. Підсумки уроку
На якому з рисунків (див. рис. 2) допущені помилки в зображенні прямокутного трикутника?
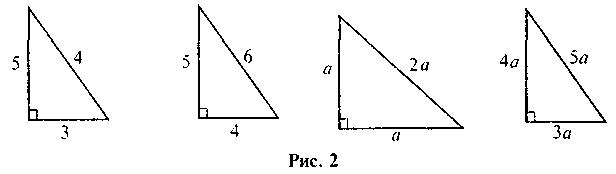
VIII. Домашнє завдання
Вивчити зміст та доведення теореми Піфагора.
Розв’язати задачі.
1. У прямокутнику знайдіть діагональ, якщо сторони дорівнюють 10 см і 24 см.
2. Периметр рівнобедреного трикутника дорівнює 36 см, а бічна сторона – 13 см. Знайдіть медіану трикутника, проведену до основи.
3. У прямокутному трикутнику знайдіть невідомі сторони, якщо:
А) катет і гіпотенуза відносяться як 12 : 13, а другий катет дорівнює 10см;
Б) катет більший за свою проекцію на гіпотенузу на 8 см, а висота, проведена до гіпотенузи, дорівнює 24 см.
4. Основи прямокутної трапеції дорівнюють 21 см і 28 см, а більша бічна сторона – 25 см. Знайдіть периметр трапеції. Чи можна вписати в неї коло?
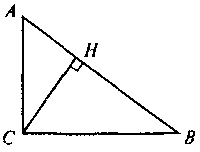
 АСВ = 90°, СН
АСВ = 90°, СН АВ. Знайдіть:
АВ. Знайдіть: