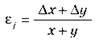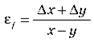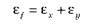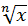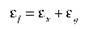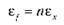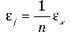Вимірювання. Похибки вимірів. Математика
1-й семестр
ВСТУП
Урок 2/2
Тема. Вимірювання. Похибки вимірів. Математика – мова фізики
Мета уроку: ознайомити учнів з поняттям “похибка вимірювань”. Ознайомити учнів з математичним апаратом у курсі фізики
Тип уроку: вивчення нового матеріалу
План уроку
Вивчення нового матеріалу | 40 хв. | 1. Похибки вимірювань. Абсолютна та відносна похибки вимірювання. 2. Як визначають абсолютну та відносну похибки непрямих вимірювань. 3. Як правильно записати результат 4. Скалярні й векторні величини. 5. Наближені обчислення. 6. Графіки функцій та правила їх побудови |
Закріплення вивченого матеріалу | 5 хв. | Розв’язування задач |
ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ
1. Похибки вимірювань. Абсолютна та відносна похибки вимірювання
Під час вимірювання будь-якої фізичної величини зазвичай виконують три послідовні операції:
1) вибір, перевірка й встановлення приладів;
2) фіксування показань приладів;
3) обчислення шуканої величини за результатами вимірювань, оцінка похибки.
Значення будь-якої фізичної
O Похибка вимірювання – оцінка відхилення величини вимірюваного значення величини від Ті справжнього значення. Похибка вимірювання є мірою точності вимірювання.
Помилки у вимірюванні фізичних величин поділяють на два класи: випадкові похибки й систематичні похибки.
Випадкові похибки зобов’язані своїм походженням ряду причин, дія яких неоднакова в кожному досліді й може бути не врахована. Випадкова похибка – похибка, що змінюється (за величиною та за знаком) від вимірювання до вимірювання. Випадкові похибки можуть бути пов’язані:
– з недосконалістю приладів (тертя в механічних приладах і т. п.);
– тряскою в міських умовах;
– з недосконалістю об’єкта вимірювання (наприклад, під час вимірювання діаметра тонкого дроту, який може мати не зовсім круглий перетин у результаті недосконалості процесу виготовлення);
– з особливостями самої вимірюваної величини.
Припустимо, що використовуючи ту ж саму апаратуру і той самий метод вимірювання, визначили N вимірювань величини х і отримали N значення, де величина х1 – результат першого вимірювання, х2 – другого, xN – N – го виміру.
Щоб проаналізувати результати, необхідно відповісти на два запитання:
– Як знайти найбільш імовірне значення вимірюваної величини?
– Як визначити випадкову похибку через вимірювання? Відповідь на ці запитання можна знайти в теорії ймовірностей.
Найбільш вірогідне значення вимірюваної величини (хвим) дорівнює середньому арифметичному значень, отриманих у результаті вимірів: випадкова похибка – середня помилка, отримана в результаті всіх вимірювань, обчислюється за формулою:
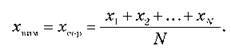
O Систематична похибка – похибка, що змінюється в часі, підпорядковуючись певному закону.
Систематичні похибки можуть бути пов’язані з помилками приладів (неправильна шкала, калібрування і т. п.),які не враховувалися експериментатором.
Щоб правильно оцінити точність експерименту, необхідно врахувати як систематичну похибку, яка є результатом роботи приладу, так і випадкову похибку, зумовлену помилками вимірювань. Цю сумарну похибку називають абсолютною похибкою вимірювання.
Сама по собі абсолютна похибка не розкриває якість вимірювання. Тому є сенс говорити про відносну похибку.
Відносна похибка характеризує якість вимірювання й дорівнює відношенню абсолютної похибки до середнього значення вимірюваної величини. Відносну похибку іноді називають точністю. Найчастіше відносну похибку визначають у відсотках.
2. Як визначають абсолютну та відносну похибки непрямих вимірювань
Багато фізичних величин неможливо виміряти безпосередньо, їх непряме вимірювання має два етапи. Спочатку вимірюють величини х, у, z, які можна виміряти методом прямих вимірювань, а потім, використовуючи значення вимірювань х, у, z обчислюють шукану величину f. Нижче в таблиці виведено формули обчислення відносної похибки для деяких функцій.
Вид формули | F = x + y | F = х – у | F = ху |
Відносна похибка |
|
|
|
Вид формули | F = x/y | F = xn | F = |
Відносна похибка |
|
|
|
Абсолютну похибку (?f) можна знайти, скориставшись визначенням відносної похибки (?f). Використовуючи визначення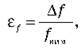 
отримуємо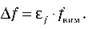 
3. Як правильно записати результат вимірювання
Абсолютна похибка експерименту визначає точність, з якою можна проводити обчислення величини, що вимірюється. Якщо помилка округлення більша за абсолютну похибку – округлення зменшує фактично досягнуту точність вимірювання; а якщо помилка округлення менша за абсолютну похибку – останні цифри запису результату будуть недостовірними. Тому округлювати результати вимірів та обчислень треба так, щоб остання значуща цифра була в тому ж десятковому розряді, що й абсолютна похибка вимірювання величини, що знаходилася.
У шкільних лабораторних роботах можна обмежуватися двома значущими цифрами. Остаточний результат для значення величини записують у вигляді: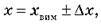 
де хвим – виміряне (середнє) значення.
4. Скалярні та векторні величини
Якщо деяка величина цілком визначається її числовими значеннями, то її називають скалярною. Прикладами скалярних величин можуть служити: маса, густина, робота, сила струму, температура.
Скалярні величини є алгебраїчними величинами, які можуть застосовуватися під час будь-яких алгебраїчних дій: додавання, віднімання, множення, ділення, знаходження ступеня і т. ін.
Якщо під час визначення певної величини для її повної характеристики, крім числового значення, треба знати й її напрям, то така величина називається векторною, або вектором.
Прикладами векторних величин є швидкість, прискорення, сила. Довжина вектора називається також його модулем або абсолютною величиною. Вектор позначається графічно відрізком прямої, на який ставиться стрілка, що вказує на напрям вектора.
Будемо позначати вектор однією буквою зі стрілкою над нею, наприклад швидкість v. Модуль вектора швидкості позначають так: v. Вектор дорівнює нулю, якщо його модуль дорівнює нулю. Такий вектор називається нульовим. Два вектори а та b називаються рівними, якщо:
1) рівні їх модулі,
2) вони паралельні і
3) спрямовані в один бік.
Два вектори з рівними модулями, що лежать на паралельних прямих, але протилежно спрямовані, називаються протилежними. Вектор, протилежний вектору а, позначається через –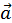
.
Дії з векторними величинами виконуємо за правилами дій з векторами. Наприклад, складання векторних величин проводиться або за правилом трикутника (рис. а), або за правилом паралелограма (рис. б).
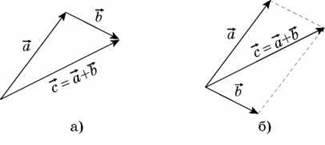
Розв’язування багатьох задач, у яких використовуються векторні величини, значно спрощується, завдяки тому, що будь-яку векторну величину можна задати за допомогою декількох чисел, які звуться проекціями цієї векторної величини на осі координат. Якщо вектор напрямлений вздовж якої-небудь однієї з координатних осей – його проекція на цю вісь дорівнює модулю цього вектора, взятому зі знаком “+”, якщо вектор напрямлений у позитивному напрямі координатної осі, і модулю вектора зі знаком “-“, якщо вектор напрямлений у негативному напрямі осі. Проекції ж такого вектора на решту координатної осі дорівнюють нулю. На рисунку як приклад зображені вектори 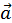і 
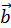, напрямлені вздовж осі х. Проекція вектора 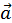на вісь х позитивна, тому ах = а, а проекція вектора 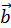– негативна, тому bх = – b.
Якщо напрям вектора не збігається з напрямом якої-небудь з координатних осей, його можна подати у вигляді суми векторів, кожен з яких напрямлений уздовж однієї з координатних осей. Таке уявлення називається розкладанням вектора на складові. У такому випадку проекції вектора – це проекції його складових. На рисунку показано розкладання вектора на складові, одна з яких напрямлена вздовж осі х, а інша – уздовж осі у.
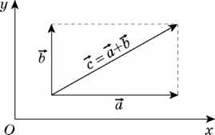
Проекції вектора с такі: сх = ах; сy = by.
5. Наближені обчислення
Виконуючи обчислення, завжди необхідно пам’ятати про ту точність, яку потрібно або яку можна отримати. Неприпустимо вести обчислення з великою точністю, якщо дані завдання не допускають або не вимагають цього. Якщо наближене число містить зайві (або невірні) знаки, то його слід округлити. Під час округлення зберігаються тільки правильні знаки; зайві знаки відкидаються. Причому якщо остання цифра більша або дорівнює 5, то попередня цифра збільшується на одиницю, а якщо остання цифра менша 5, то попередня цифра не змінюється. При округленні виникає додаткова похибка, що не перевищує половини одиниці розряду останньої значущої цифри округленого числа. Тому, щоб після округлення всі знаки були правильними, похибка до округлення повинна бути не більшою за половину одиниці того розряду, до якого робитиметься округлення.
6. Графіки функцій та правила їх побудови
Розглянемо побудову графіків двох простих функцій: лінійної функції y = y0 + kx і квадратичної функції у = ах2 + bх + с. Прикладом функцій такого виду може служити залежність переміщення від часу під час рівномірного руху (лінійна функція) і під час рівноприскореного руху (квадратична функція). Загальний метод побудови графіків будь-якої функції наступний: для функції, графік якої потрібно побудувати, складають таблицю. В одному рядку цієї таблиці записують значення аргументу (х), а в іншій – обчислені для цього аргументу значення функції. Потім будують осі координат: вісь х – вісь абсцис, і вісь у – вісь ординат. Після цього відкладають точки з парою координат (хi, yi) з таблиці і через отримані точки проводять плавну криву.
Графіком лінійної функції є пряма лінія. Для його побудови досить знайти положення двох точок і через ці точки провести пряму лінію. Графіком квадратичної функції є парабола, для побудови якої необхідно: знайти точки перетину графіка з осями координат; знайти вершину параболи; побудувати вісь симетрії.
ЗАКРІПЛЕННЯ ВИВЧЕНОГО МАТЕРІАЛУ
1. Які послідовні операції виконують, вимірюючи будь-яку величину?
2. Що таке прямі вимірювання? Наведіть приклади.
3. Що таке непрямі вимірювання? Наведіть приклади.
4. З якою метою необхідно оцінювати точність вимірів?
5. Наведіть приклади випадкових похибок; систематичних похибок.
6. Наведіть приклади абсолютної та відносної похибок.
7. Для чого необхідно робити оцінку абсолютної похибки?
8. Які величини називаються скалярними? Наведіть приклади скалярних величин у фізиці.
9. Які величини називаються векторними? Наведіть приклади векторних величин у фізиці.
10. Що таке проекція векторної величини на вісь координат? Який знак може мати ця проекція?
Задачі для розв’язування на уроці
1. Тіло перемістилося з певної точки з координатами х0 = 2 м, y0 = 3 м у точку з координатами х = 4 м і у = 1 м. Знайдіть модуль вектора та його проекції на осі координат.
2. Тіло перемістилося з певної точки з координатами x1 = 0, у1 = 2 м у точку з координатами х2 = 4 м і у2 = -1 м. Знайдіть модуль вектора та його проекції на осі координат.
Що ми дізналися на уроці
– Похибка вимірювання – оцінка відхилення величини виміряного значення величини від її справжнього значення. Випадкові похибки зобов’язані своїм походженням ряду причин, дія яких неоднакова в кожному досліді й не може бути врахована. Найбільш вірогідне значення вимірюваної величини (хвим) дорівнює середньому арифметичному значень, отриманих у результаті вимірів.
– Випадкова похибка (?хвим) – середня помилка, отримана в результаті всіх вимірювань,- обчислюється за формулою:
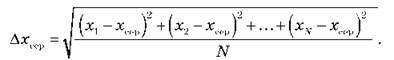
– Відносна похибка характеризує якість вимірювання й дорівнює відношенню абсолютної похибки (?х) до середнього значення вимірюваної величини (хвим):
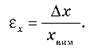
– Абсолютна похибка – це модуль відхилення виміряного значення фізичної величини від її справжнього значення:
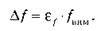
Домашнє завдання
1. П.: Вступ. §§ 3, 4.
2. 36:
Р1) – 1.5; 1.8. 1.12; 1.13; 1.18;
Р2) – 1.21;1.22;1.24, 1.26;
Р3) – 1.34,1.35, 1.37,1.38.
(1 votes, average: 5.00 out of 5)
Loading...