Властивість медіани, бісектриси й висоти рівнобедреного трикутника
Урок № 25
Тема. Властивість медіани, бісектриси й висоти рівнобедреного трикутника
Мета: домогтися свідомого сприйняття учнями змісту теореми про властивість медіани, бісектриси й висоти рівнобедреного трикутника та наслідків з неї; сформувати вміння відтворювати названі властивості та застосовувати їх під час розв’язування задач.
Тип уроку: засвоєння знань, умінь та навичок.
Наочність і обладнання: набір демонстраційного креслярського приладдя; таблиця; роздавальний матеріал.
ХІД УРОКУ
I. Організаційний момент
II.
Домашнє завдання перевіряємо в учнів, які потребують додаткової педагогічної уваги.
III. Актуалізація опорних знань
Практична робота за готовими рисунками
1. Перевірте, чи є трикутник рівнобедреним. Якщо так, назвіть та запишіть його основу, бічні сторони.
2. З вершини, протилежній до основи, проведіть послідовно:
А) медіану;
Б) бісектрису;
В) висоту.
Що ви помітили? Сформулюйте гіпотезу.
3*. З вершин при основі проведіть:
А) медіани, порівняйте їх довжини;
Б) бісектриси, порівняйте їх довжини;
В) висоти, порівняйте їх довжини.
Що ви помітили?
Методика проведення практичної роботи
Кожен учень (або мала група – на розсуд учителя) отримує аркуш із зображенням рівнобедреного трикутника та виконує послідовно завдання практичної роботи. Після виконання роботи групи презентують свої гіпотези, відбувається осмислене цілепокладання уроку (вчитель може зібрати аркуші та оцінити вміння учнів виконувати побудови медіан, бісектрис та висот трикутника.)
V. Засвоєння нових знань
План вивчення нового матеріалу
1°. Формулювання теореми про медіану, бісектрису, висоту рівнобедреного трикутника.
2°. Наслідок з теореми.
3°. Застосування теореми:
А) для доведення того, що трикутник рівнобедрений [метод подвоєння медіани];
Б) для виконання зображення рівнобедреного трикутника.
Метод подвоєння медіани не є обов’язковим для розглядання, але можна його вивчити в класах з високим рівнем підготовки учнів і бажано підкріпити задачним матеріалом.
Також важливим є питання про практичне застосування теореми про медіану, бісектрису, висоту рівнобедреного трикутника, а саме: як побудувати рівнобедрений трикутник на практиці?
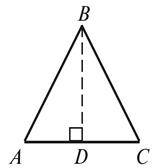
1. Будуємо довільний відрізок, AC – основа.
2. Ділимо відрізок AC навпіл, D – середина AC.
3. Через точку D проведемо перпендикуляр до AC. На прямій позначимо точку B.
4. Δ ABC – шуканий рівнобедрений.
VI. Первинне усвідомлення нового матеріалу
Виконання усних вправ
1. У трикутнику ABC відрізок AD – медіана, бісектриса й висота. Назвіть рівні сторони трикутника.
2. У трикутнику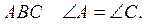 
Бісектриса якого з кутів трикутника збігається з медіаною та висотою?
3. У рівнобедреному, але не рівносторонньому трикутнику проведено всі медіани, бісектриси й висоти. Скільки різних відрізків проведено? Як зміниться відповідь, якщо даний трикутник є рівностороннім?
4. У трикутнику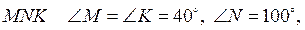 
NP – медіана. Знайдіть кути ΔMNP.
5. Як у рівнобедреному трикутнику OMK з основою OK провести висоту (бісектрису) з вершини M, використовуючи тільки лінійку з поділками?
Виконання письмових вправ
1. Накресліть рівнобедрений трикутник ABC з основою AC і тупим кутом B.
А) Проведіть висоту AD. Чи лежить точка D на відрізку BC?
Б) Проведіть медіану BM. Чи є рівними кути ABM і CBM? Чому?
2. У трикутнику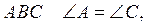 
BD – бісектриса трикутника. Доведіть, що AD = CD.
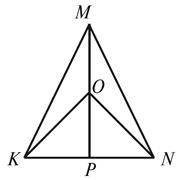
3. На висоті MP рівнобедреного трикутника KMN з основою KN позначено точку O (рис. 1). Доведіть, що трикутник KON рівнобедрений.
4. Доведіть, що медіани рівних трикутників, проведені до відповідно рівних сторін, рівні.
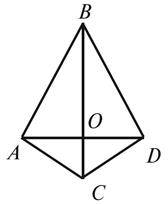
5. Трикутники ABC і DBC рівні (рис. 2). Доведіть, що точка перетину відрізків AD і BC ділить відрізок AD навпіл.
Підчасрозв’язуваннязадачслідвимагативідучнівзастосуваннясформульованих на уроці тверджень для аргументації своїх міркувань якомога частіше. Також бажано продовжувати розпочату на попередніх уроках роботу щодо формування вмінь міркувати “від кінця до початку” (там, де це доречно – у задачах достатнього та високого рівня).
VII. Підсумки уроку
Чи правильне твердження: “Медіана рівнобедреного трикутника збігається з висотою та бісектрисою”?
VIII. Домашнє завдання
Усно виконати вправу.
Чи може медіана трикутника збігатися з його висотою, але не збігатися з бісектрисою, проведеною з тієї самої вершини?
Письмово розв’язати задачі.
1. У трикутнику ABC відрізок CD є медіаною й висотою. Доведіть, що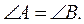 
2. У рівнобедреному трикутнику KON з основою KN на продовженні бісектриси OP позначено точку M (рис. 3). Доведіть, що трикутник KMN рівнобедрений.
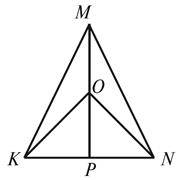
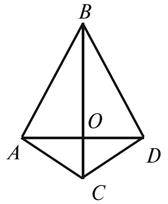
3. Перпендикулярні відрізки AD і BC перетинаються в точці O, причому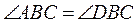 
(рис. 4). Доведіть, що трикутник ACD рівнобедрений.
Джерела:
1. Уроки геометрії. 7 клас./ С. П. Бабенко – Х.: Вид. група “Основа”, 2007.- 208 с.
(1 votes, average: 5.00 out of 5)
Loading...