Властивості додавання
Розділ 4 Раціональні числа і дії мідними
§40. Властивості додавання
Для додавання раціональних чисел, як і для додавання додатних чисел, справджуються переставна і сполучна властивості.
Переставна властивість додавання.
Для будь-яких раціональних чисел а і b виконується рівність а + b = b + а.
Перевіримо цю властивість на прикладах.
Приклад 1. -8 + (-3) = -11; -3 + (-8) = -11, тому -8 + (-3) = -3 + (-8).
Приклад 2. -2 + 5 = 3; 5 + (-2) = 3, тому -2 + 5 = 5 + (-2).
Сполучна властивість додавання.
Для будь-яких раціональних чисел а, b і c виконується рівність (а
Перевіримо цю властивість на прикладі.
Приклад 3. (-2 + 7) + (-8) = 5 + (-8) = -3; -2 + (7 + (-8)) = -2 + (-1) = -3, тому (-2 + 7) + (-8) = -2 + (7 + (-8)).
Для будь-якого раціонального числа а виконуються рівності: а + 0 = 0 + а = а; а + (-а) = – а + а =0.
Властивості додавання дають можливість спростити процес обчислення суми кількох доданків, обираючи зручний порядок обчислень. Якщо необхідно додати кілька чисел, серед яких є додатні і від’ємні числа, то можна окремо додати всі додатні числа і окремо всі від’ємні, а потім до суми додатних чисел додати суму від’ємних. Якщо серед доданків є протилежні числа, то сума цих доданків дорівнює
Приклад 4. Обчислити суму:
-7 + (-4) + 11 + (-5) + 7 + (-12) + 8 + 1.
Розв’язання. Зазначимо, що серед доданків є протилежні числа: -7 і 7, сума яких дорівнює нулю. Їх можна закреслити. Далі згрупуємо числа з однаковими знаками:
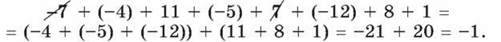
У чому полягають переставна та сполучна властивості додавання? ) Чому дорівнює x + 0; x + (-x)?
1061. (Усно) Обчисли, враховуючи, що а + (-а) = 0:
1) 7 + (-7) + 8; 2) -11 + (-9) + 9; 3) -2 + 9 + 2.
1062. Знайди суму:
1) 4 + (-4); 2) -17 + 17 + (-2); 3) -4 + (-8) + 4.
1063. Перевір переставну властивість додавання а + b = b + а, якщо:
1) а = -5; b = 7; 2) а = 4; b = -8; 3) а = -4; b = -7.
1064. (Усно) Обчисли:
1) 5 + (-3) + 2; 2) -7 + 2 + (-1);
3) -4 + (-2) + 5; 4) 6 + (-3) + (-5) + 2.
1065. Виконай додавання, обираючи зручну послідовність обчислень:
1) -8 + 7 + (-7) + 8;
2) 43 + (-20) + (-37) + 20;
3) -3,63 + 4,28 + 2,72 + (-7,37);
4) -1,48 + 5 + 1,48 + (-7) + 2.
1066. Виконай додавання, обираючи зручну послідовність обчислень:
1) -19 + 11 + (-11) + 19;
2) -41 + (-17) + 37 + 17;
3) 3,47 + (-1,11) + (-8,89) + 5,53;
4) 1,5 + (-8) + (-1,5) + 7 + (-2).
1067. Перевір сполучну властивість додавання (а + b) + c = а + (b + c), якщо:
1) а = -5; b = 7; c = -9; 2) а = 11; b = -7; c = -3.
1068. Перевір сполучну властивість додавання (а + b) + c = а + (b + c), якщо:
1) а = -8; b = -7; c = 19; 2) а = 14; b = 17; c = -40.
1069. Знайди значення виразу:
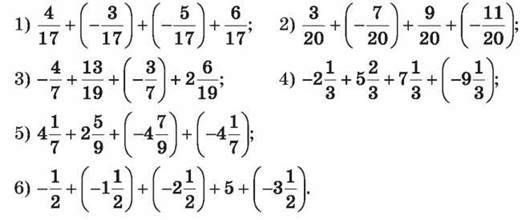
1070. Обчисли:
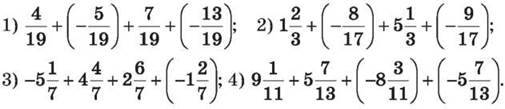
1071. Обчисли значення виразу x + (-3) + у, якщо: 1) x = -8,5; у = 7,9; 2) x = 4; у = 1,2.
1072. Виконай додавання:
1) 12 + 15 + (-17) + (-18) + 19 + (-1);
2) -23 + 28 + (-11) + (-34) + 29 + 11;
3) -44,03 + (-62,07) + 92,13 + 1,05;
4) -1592,69 + (-29,47) + 113,92 + (-18,01).
1073. Виконай додавання:
1) -18 + (-7) + 14 + 25 + 13 + (-10);
2) 37 + (-18) + 23 + 1 + (-42) + (-5);
3) 15,7 + 16,3 + (-8,13) + (-18,5);
4) 14,5 + (-18,3) + (-17,1) + (-8,9).
1074. Заміни зірочку знаком >, < або =, щоб утворилася правильна рівність або нерівність:
1) 2 + (-7) + (-2) * 8 + (-8) + 3;
2) 14 + (-2) + (-3) * (-3) + 14 + (-2);
3) 0 + 9 + (-8) * 0 + 8 + (-9);
4) 4 + (-7) + (-4) + 7 * 11 + 1 + (-11).
1075. У касі було 1000 грн. Протягом дня касир кілька разів приймав і видавав гроші та занотував це так: -140 грн; 300 грн; -500 грн; -120 грн; 180 грн; 320 грн. Скільки гривень стало в касі в кінці дня?
1076. На складі було 45 банок з фарбою. Протягом дня комірник кілька разів приймав і видавав банки з фарбою та зробив такі записи: 12 банок; -18 банок; 7 банок; -8 банок; -11 банок. Скільки банок з фарбою стало на складі в кінці дня?
1077. Знайди суму всіх цілих чисел, що розміщені на координатній прямій між числами:
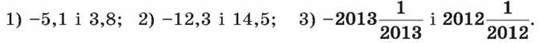
1078. Знайди суму всіх цілих чисел, що задовольняють нерівність:
1) -4,17 < x < 5,91; 2) -12,5 < x < 10,7.
1079. Виконай дії:
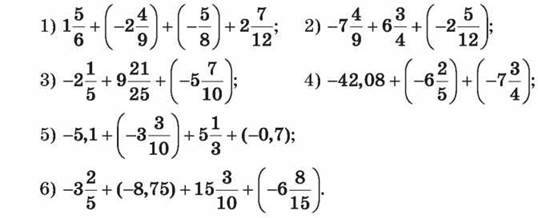
1080. Знайди значення виразу:
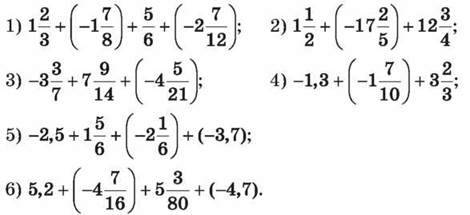
1081. Спрости вираз і знайди його значення:
1) -9,6 + х + 4,42 + (-1,8) + 1,13, якщо х = 5; -1,7;
2) 4,31 + (-2,42) + а + (-1,17) + (-1,18), якщо а = -0,8; 0,47;
3) 5,42 + x + (-2,17) + (-2,38) + у + 1,18, якщо x = -1,13; у = 1,19.
1082. Спрости вираз і знайди його значення:
1) 5,7 + (-4,8) + а + 1,17 + (-3,92), якщо а = 1,19; -2,32;
2) 4,47 + m + (-2,37) + n + (-0,32) + 1,12, якщо m = -3,17; n = 0,27.
1083. Дано числа 9; -8; 7,3; -6,7; -5 і 1,4. Знайди:
1) число, протилежне до суми цих чисел;
2) суму чисел, протилежних до даних чисел;
3) суму модулів цих чисел;
4) модуль суми цих чисел.
1084. Дано числа 1,8; -2,3; 4,7; -5,8; -4,1. Знайди:
1) число, протилежне до суми цих чисел;
2) суму чисел, протилежних до даних чисел.
1085. За якої умови рівність а + b + c + d = 0 буде правильною, якщо а і d – протилежні числа?
1086. За 0 ,8 кг печива заплатили 23,04 грн. Скільки треба заплатити за 1,5 кг такого печива?
1087. Андрій під час канікул мав розв’язати 28 задач, а розв’язав 35 задач. Скільки відсотків завдання він виконав і на скільки відсотків перевиконав?
1088. Три однакових за вагою яблука важчі, ніж чотири однакові груші. Що важче: 4 яблука чи 5 груш?