Головна ⇒ 📌ГДЗ з математики ⇒ Властивості кола. Дотична до кола

Властивості кола. Дотична до кола

§ 3. Паралельні прямі. Сума кутів трикутника

§ 19. Властивості кола. Дотична до кола

Практичні завдання

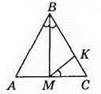
507. АК = КВ.

Властивості кола. Дотична до кола

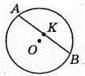
508. AB ⊥ CD – дотичні до кола.

Властивості кола. Дотична до кола

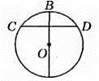
509. АС i ВС – дотичні до кола.

Властивості кола. Дотична до кола

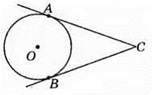
510. Таких кіл може бути два.

Властивості кола. Дотична до кола

Вправи

511. CD ⊥ AB. ?АОК = ?ВОК (за катетом і гіпотенузою: ОК – спільний катет, ОА = OB – як радіуси кола), тоді ∠AOD = ∠BOD.

Властивості кола. Дотична до кола

512. Нехай AB = CD, OM ⊥ AB, ON ⊥ CD. Доведемо, що ОМ

= ON.

Оскільки ОМ ⊥ AB, то AM = MB; оскільки ON ⊥ CD, то CN = ND.

?ОМА = ?ONC (за гіпотенузою і катетом: АО = СО – як радіуси, AM = CN – як половини рівних відрізків), тоді ОМ = ON.

Властивості кола. Дотична до кола

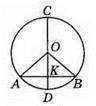
513. Якщо хорди рівновіддалені від центра кола, то вони рівні. Нехай ОМ ⊥ AB, ON ⊥ CD і ОМ = ON. Доведемо, що AB = CD.

Оскільки ОМ ⊥ AB, ON ⊥ CD, то AM = MD, CN = ND, тобто щоб довести, що AB = CD, достатньо довести, що AM = CN.

?АОМ = ?CON (за гіпотенузою і катетом: ОМ = ON за умовою, АО = ОС – як радіуси кола), тоді AM = CN. Отже, AB = 2AM = 2CN = CD.

514. Hi. Наприклад АВ ⊥ OM, але АВ не дотична.

Властивості кола. Дотична до кола

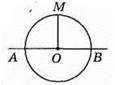
Дотична до кола перпендикулярна

до радіуса, проведеного в точку дотику.

Властивості кола. Дотична до кола

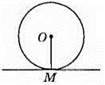
515. ∠OAB = 90° – ∠BAD = 90° – 35° = 55°, АО = OB, тому ∠OBA = ∠OAB = 55°, ∠AOB = 180° – 2 • 55° = 180° – 110° = 70°.

Відповідь: 70°.

516. ∠OAB = ∠OBA, тому ∠OAB = 1/2. (180° – 80°) = 50°, ∠BAC = ∠OAB + ∠OAC = 50° + 90° = 140°.

Відповідь: 140°.

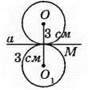
517. Радіус кола дорівнює 1/2 • 6 = 3 (см). Тому пряма а є дотичною у випадку 2).

518. 1) АС є радіусом, АС ⊥ СВ, тому СВ – дотична;

2) AB не перпендикулярна до радіуса АС, тому вона не є дотичною.

Властивості кола. Дотична до кола

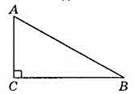
519. СВ = СО + ОВ = АО + OB > АВ.

Властивості кола. Дотична до кола

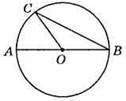
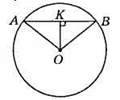
520. ОС ⊥ AB, OK = CK.

Із прямокутного? АОК маємо: ∠OAK = 30° (оскільки АО = 2ОК).

Із прямокутного? ВОК маємо: ∠OBK = 30° (оскільки ВО = 2ОК).

∠AOB = 180° – ∠OAB – ∠OBA = 180° – 30° – 30° = 120°.

Властивості кола. Дотична до кола

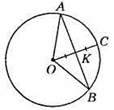
521. 1) OK = 1/2AB.

?АОК = ?ВОК (за катетом і гіпотенузою: ОК – спільний катет, ОА = ОВ – як радіуси кола). AK = КВ, тому ОК = KB; ∠KOB = 45°; ∠AOB = 2 х 45° = 90°.

Відповідь: 90°.

2) OK = 1/2OB, тому ∠OBK = 30°; ∠OAK = ∠OBK =30°, ∠AOB = 180° – 30° – 30° = 120°.

Властивості кола. Дотична до кола

Відповідь: 120°.

522. АС = 12 см, ∠CAB = 30°.

З? АСК: 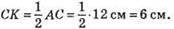Властивості кола. Дотична до кола

CK = KB – оскільки AB ⊥ CD. Отже, CD = 2СK = 2 х 6 = 12 см.

Властивості кола. Дотична до кола

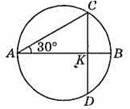
Відповідь: 12 см.

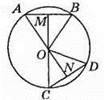
523. ∠OBA = ∠OAB = 20°.

∠BAM = ∠OAM – ∠OAB = 90° – 20° = 70°. ∠ABM = ∠OBM – ∠OBA = 90° – 20° = 70°.

Тоді ∠AMB = 180° – ∠BAM – ∠ABM = 180° – 70° – 70° = 40°.

Властивості кола. Дотична до кола

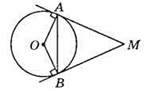
Відповідь: 40°.

524. OA = OB = AB. Тому ∠OAB = ∠OBA = 60°. ∠CAB = ∠CBA = 90° – 60° = 30°. ∠ACB = 180° – 30° – 30° = 120°.

Властивості кола. Дотична до кола

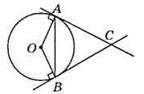
Відповідь: 120°.

525. ОА = ОС, отже, ?OAC – рівнобедрений.

∠OAC = ∠OCA, ∠OCA = ∠CAD, тому ∠OAC = ∠CAD, отже, CD – бісектриса ∠BAD.

Властивості кола. Дотична до кола

526.

Властивості кола. Дотична до кола

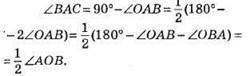
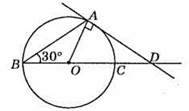
527. ∠ABC = 30°. ∠AOD – зовнішній кут? АОВ; ∠AOD = ∠OBA + ∠OAB = 30° + 30° = 60°; ∠ADB = 90° – ∠AOD = 90° – 60° – 30°. Отже, ∠ABD = ∠ADB, тому? ABD – рівнобедрений.

Властивості кола. Дотична до кола

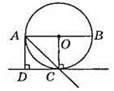
528. Якщо б хорда CD не була діаметром, то діаметр AB, який ділить її навпіл, був би перпендикуляром до неї, але це не так. Тому CD – діаметр.

529. Геометричним місцем центрів кіл, які дотикаються до даної прямої в даній точці є перпендикулярна пряма до даної прямої, яка проходить через дану точку.

Властивості кола. Дотична до кола

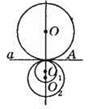
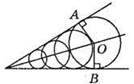
530. Геометричним місцем центрів кіл, які дотикаються до обох сторін кута, є бісектриса цього кута.

Властивості кола. Дотична до кола

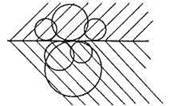
531. Геометричним місцем центрів кіл, які дотикаються до даної прямої є усі точки площини, за винятком самої прямої.

Властивості кола. Дотична до кола

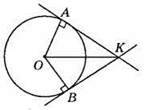
532. ∠AKB = 120°. ?ОАК = ?ОВК (за гіпотенузою і катетом: ОК – спільна, ОA = OB – як радіуси), тому ∠AKO = ∠BKO = 120° : 2 = 60°, АК = ВК.

З? ОАК: ∠AOK = 90° – ∠AKO = 90° – 60° = 30°. Отже, OK = 2АК, або OK = АК + ВК.

Властивості кола. Дотична до кола

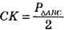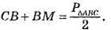
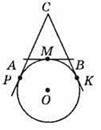
533. AM = АР – як відрізки дотичних, проведених із однієї точки до кола, ВМ = BK, CP = СК – як відрізки дотичних, проведених із однієї точки до кола. Р? ABC = АС + CB + AB = АС + СВ + AM +MB = АС + CB + АР + ВК = (АС + АР) + (СВ + ВК) = СР + СК. Оскільки СР = СК, то маємо: Р? ABC = 2 x СК, звідки Властивості кола. Дотична до кола або Властивості кола. Дотична до кола

Властивості кола. Дотична до кола

534. Р? DEC = CD + СЕ + DE = CD + СЕ + DM + EM. Оскільки DM = DA, BE = EM – як відрізки дотичних, проведених із однієї точки до кола, то маємо Р? DEC = CD + СЕ + DA + BE = (CD + DA) + (CE + BE) = CA + CB. Отже, периметр трикутника DEC не залежить від вибору точки М.

Вправи для повторення

535. М – середина відрізка AB, а || b.

Властивості кола. Дотична до кола

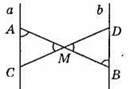
?АМС = ?BMD – за стороною і двома прилеглими кутами: АМ = ВМ, ∠AMС = ∠CBMD – як вертикальні кути, ∠А = ∠B як внутрішні різносторонні кути при паралельних прямих а і b і січній AB). Із рівності цих трикутників випливає, що CM = DM.

536. AN = NB, СN = CD. Оскільки? AMB – рівнобедрений і MN є медіаною, то MN є і висотою.

?CMN = ?DMN (за вдома катетами: MN – спільний катет, CN = ND за умовою). Із рівності цих трикутників випливає, що MC = MD, тобто? CMD – рівнобедрений.

Властивості кола. Дотична до кола

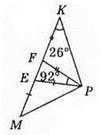
537. ME = ЕР, FK = FP, ∠К = 26°, ∠EPF = 92°.

?KFP – рівнобедрений, оскільки FK = FP. Отже, ∠KPF = ∠К = 26°.

∠EFP – зовнішній кут? EFP, ∠EFP = ∠К + ∠КРЕ = 26° + 26° = 52°.

∠МЕР – зовнішній кут? EFP, ∠МЕР = ∠EFP + ∠EPF = 52° + 92° = 144°.

Оскільки? МЕР – рівнобедрений, то ∠М = (180° – ∠МЕР): 2 = (180° – 144°) : 2 = 18°.

Властивості кола. Дотична до кола

Відповідь: 18°.

538. ВМ – бісектриса ∠АВС, ∠АВМ = ∠МВС = α. Тоді ∠КМС = α.

З? МКС: ∠С = 90° – α. З? АВС: ∠А = 180° – ∠В – ∠С = 180° – 2α – (90° – а) = 180° – 2α – 90° + α = 90° – α. Отже, ∠А = ∠С, тобто? АВС – рівнобедрений.

Властивості кола. Дотична до кола


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Дотична до кола, її властивості Розділ 4. Коло і круг. Геометричні побудови § 22. Дотична до кола, її властивості 607. Проведемо радіус ОР, а потім за допомогою косинця побудуємо пряму m, перпендикулярну до радіуса. За теоремою 2 пряма m є дотичною до кола. 608. Проведемо радіус ОМ, а потім за допомогою косинця побудуємо пряму n, перпендикулярну до радіуса. За теоремою […]...

  2. Дотична до кола Урок № 43 Тема. Дотична до кола Мета: вивчити означення дотичної до кола, теореми про властивість та ознаку дотичної до кола. Сформувати вміння: – відтворювати формулювання означення, властивості та ознаки дотичної; – використовувати ці формулювання під час розв’язування задач. Тип уроку: засвоєння знань, умінь та навичок. Наочність і обладнання: набір демонстраційного креслярського приладдя; таблиця “Дотична […]...

  3. Властивості прямокутного трикутника § 3. Паралельні прямі. Сума кутів трикутника § 17. Властивості прямокутного трикутника 457. Найбільший катет трикутника дорівнює 24 см. 458. ?DEF – прямокутний, ∠F = 90°, ∠D = 30°, DE = 18 см. Відповідь: 9 см. 459. ?KCM – прямокутний, ∠M = 90°, ∠C = 60°, MC = 7 см. ∠MKC = 90° – 60° […]...

  4. Ознаки рівнобедреного трикутника § 2. Трикутники 9. Ознаки рівнобедреного трикутника 232. ?ABC – рівнобедрений, тому ВК є бісектрисою кута ABC, отже, ∠ABC = 2 х ∠ABK = 2 x 25° = 50°. Відповідь: 50°. 233. BK є висотою та медіаною, тому? ABC – рівнобедрений, AB = ВС, отже, ∠C = ∠A =17°. Відповідь: 17°. 234. AС = ВС, […]...

  5. Описані і вписані кола Розділ 1. Найпростіші геометричні фігури та їх властивості § 17. Описані і вписані кола 671. Коло, описане навколо трикутника, зображено на мал. 372. 672. Коло, вписане у трикутник, зображено на мал. 375. 673. Центр кола, описаного навколо гострокутного трикутника, лежить всередині трикутника. Центр кола, описаного навколо прямокутного трикутника, лежить на середині гіпотенузи. Центр кола, описаного […]...

  6. Описане та вписане коло трикутника § 3. Паралельні прямі. Сума кутів трикутника § 20. Описане та вписане коло трикутника 540. 1) Різносторонній гострокутний трикутник. 2) Прямокутний трикутник. 3) Тупокутний трикутник. 541. 1) Рівнобедрений гострокутний трикутник. 2) Рівнобедрений тупокутний трикутник. 542. 543. 544. Вправи 545. Медіана BD рівнобедреного трикутника ABC є в той же час і серединним перпендикуляром до сторони АС […]...

  7. Зовнішній кут трикутника та його властивості Розділ 3. Трикутники. Ознаки рівності трикутників § 18. Зовнішній кут трикутника та його властивості 438. ∠BAK – зовнішній кут при вершині А. 439. ∠LDP – зовнішній кут при вершині D. 441. ∠A + ∠B = 70° – за властивістю зовнішнього кута трикутника. 442. Зовнішній кут трикутника при вершині С дорівнює 74° згідно з властивістю зовнішнього […]...

  8. Довжина кола і дуги кола УРОК № 20 Тема. Довжина кола і дуги кола Мета уроку: виведення формул для знаходження довжини кола та довжини дуги кола. Формування вмінь учнів застосовувати виведені формули до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Довжина кола і площа круга” [13]. Вимоги до рівня підготовки учнів: записують і пояснюють формули довжини кола і […]...

  9. Рівнобедрений трикутник і його властивості § 2. Трикутники 8. Рівнобедрений трикутник і його властивості Практичні завдання 196. 197. 198. Вправи 199. 1) Р = 13 + 2 х 8 = 29(см). Відповідь: 29 см. 2) Нехай х см – бічна сторона, тоді 15 + 2х = 39, тоді 2х = 39 – 15; 2х = 24; х = 24 : […]...

  10. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 19. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників 466. 1) PF – гіпотенуза, PL і LF – катети. 2) PF довша за PL, PF довша за LF, оскільки PF – гіпотенуза. 467. На рис. 321 трикутники рівні за двома катетами. Оскільки АС = ML, СВ = LP, […]...

  11. Коло і його елементи Розділ 4. Коло і круг. Геометричні побудови § 21. Коло і його елементи 578. PL – хорда, що проходить через центр кола, називається діаметром. 579. 1) 5 х 2 = 10(см); 2) 4,7 х 2 = 9,4 (дм). 580. 1) 8 мм х 2 = 16 мм; 2) 4,8 см х 2 = 7,6 см. […]...

  12. Властивості й ознака рівнобедреного трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 12. Властивості й ознака рівнобедреного трикутника 476. На мал. 72: ML і МК – бічні сторони, KL – основа, ∠K = ∠L. 477. KD = DF, КЕ = EF, ∠K = ∠F, ∠KDE = ∠FDE, ∠DEK = ∠DEF = 90°. 478. Щоб провести бісектрису, медіану і […]...

  13. Властивості конуса 1. 1) Твірна конуса не може утворювати з його основою прямий кут, оскільки Вона є гіпотенузою трикутника обертання, яка утворює бічну поверхню конуса. 2) Теж не може (обгрунтування у п. 1). Якщо конус зрізаний 1) ні; 2) так. Відповідь: 1) ні; 2) ні для зрізаного конуса 1) ні, 2) так. 2. Нехай SA – твірна […]...

  14. Довжина кола Геометрія Многокутники Довжина кола Теорема. Відношення довжини кола до його діаметра не залежить від кола, тобто є одним і тим самим числом для будь-яких двох кіл. Це число позначається . , де l – довжина кола, R – радіус. Отже, або ; – число ірраціональне, . Довжина дуги кола, яка відповідає центральному куту : . […]...

  15. КОЛО, КРУГ ТА ЇХ ЕЛЕМЕНТИ. ЦЕНТР КОЛА (круга), РАДІУС, ДІАМЕТР. ПОБУДОВА КОЛА. РОЗВ’ЯЗУВАННЯ ВПРАВ І ЗАДАЧ НА ВИВЧЕНІ ВИПАДКИ АРИФМЕТИЧНИХ ДІЙ АРИФМЕТИЧНІ ДІЇ МНОЖЕННЯ ТА ДІЛЕННЯ (продовження) Урок 68. КОЛО, КРУГ ТА ЇХ ЕЛЕМЕНТИ. ЦЕНТР КОЛА (круга), РАДІУС, ДІАМЕТР. ПОБУДОВА КОЛА. РОЗВ’ЯЗУВАННЯ ВПРАВ І ЗАДАЧ НА ВИВЧЕНІ ВИПАДКИ АРИФМЕТИЧНИХ ДІЙ Мета: ознайомити учнів із кругом і колом; навчати відрізняти круг і коло; вчити працювати з циркулем; формувати вміння розв’язувати приклади і задачі на вивчені випадки арифметичних […]...

  16. Взаємне розміщення двох кіл Розділ 4. Коло і круг. Геометричні побудови § 25. Взаємне розміщення двох кіл 656. На рис. 404 кола перетинаються. На рис. 405 кола дотикаються. На рис. 406 кола не мають спільних точок. 657. 1) Кола мають внутрішній дотик. 2) Кола перетинаються. 3) Кола концентричні. 658. 1) Кола мають зовнішній дотик. 2) Кола не перетинаються. 659. […]...

  17. Властивості кутів трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 10. Властивості кутів трикутника 344. ∠E = 60°, ∠F = 40°, ∠D = 80°. ∠E + ∠F + ∠D = 60° + 40° + 80° = 180°. 345. На мал. 208 неправильно сказано градусну міру кутів? АВС, оскільки? ABC – прямокутний, a ∠B + ∠C = […]...

  18. Рівняння кола УРОК № 26 Тема. Рівняння кола Мета уроку: виведення рівняння кола. Формування вмінь учнів використовувати рівняння кола до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати і вектори на площині” [13]. Вимоги до рівня підготовки учнів: записують і пояснюють рівняння кола. Розпізнають рівняння кола. Хід уроку I. Перевірка домашнього завдання Перевірити наявність […]...

  19. Дуга кола й круговий сектор – КОЛО Формули й таблиці МАТЕМАТИКА КОЛО Р – пряма, що не має спільних точок з колом T – дотична К – радіус D – діаметр G – січна S – хорда С – довжина кола Дотична й радіус, проведений у точку дотику, перпендикулярні. B – дуга кола α – кут між дотичною і хордою β – […]...

  20. Властивості сфери і кулі 1. Відстань, яка б відділяла мене від мого антипода дорівнювала б Двом радіусам Землі. Відповідь: 2R Землі. 2. Нехай АО – радіус Землі, ОА = 6400 км, О1А – радіус Полярного кола Землі. Координати Полярного кола Землі 66°31′ п. ш. ∠АОВ = 66°31′; ∠О1ОА = 90° – 67° = 23°. З ΔO1ОA: Ο1Α = ОА […]...

  21. Коло. Довжина кола Розділ 3 Відношення і пропорції §29. Коло. Довжина кола Дуже давно люди винайшли колесо та побачили його корисні в побуті властивості. Геометричними фігурами, які дають уявлення про колесо, є коло і круг. На малюнку 15 зображено креслярський інструмент – циркуль. На одній його ніжці – вістря, а на другій – грифель. Якщо поставити ніжку з […]...

  22. Коло і круг Розділ 1. Найпростіші геометричні фігури та їх властивості § 15. Коло і круг 588. 1) Хордами є відрізки: KB, NC, KN, CB, LD. 2) Діаметрами є відрізки: LD, NC, КВ. 3) Радіусами кола є відрізки: OL, OK, ОС, OD, OB, ON. 589. Дотичні до кола: АС, CB, AB. ON ⊥ AC, ОМ ⊥ CB, OK […]...

  23. Взаємне розміщення кола і прямої – СТЕРЕОМЕТРІЯ Формули й таблиці МАТЕМАТИКА СТЕРЕОМЕТРІЯ Взаємне розміщення кола і прямої Коло і пряма не мають спільних точок. Коло і пряма мають одну спільну точку. А – дотична А – точка дотику Коло і пряма мають дві спільні точки. А – січна Рівняння кола (х – а)2 + (y – b)2 = R2, де (а, b) […]...

  24. Закон Ома для ділянки кола 7. Електрика 7.16. Закон Ома для ділянки кола Сила струму в ділянці кола прямо пропорційна напрузі на кінцях цієї ділянки й обернено пропорційна її опору. Де I – сила струму; U – напруга; R – опір. Закон Ома відкритий німецьким вченим Г. Омом у 1826 році....

  25. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника Розділ 3. Трикутники. Ознаки рівності трикутників § 15. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника 351. 1) AT – висота трикутника ABC. 2) AN – медіана трикутника ABC. 3) АР – бісектриса трикутника? AВС. 352. Оскільки AK – висота, то ∠BKA = ∠CKA = 90°. 353. Оскільки АК – бісектриса, то ∠BAK = […]...

  26. Рівняння кола Геометрія Декартові координати на площині Рівняння кола – рівняння кола з центром у точці і радіусом R. Зверніть увагу: рівняння , де , задає коло й може бути зведеним до стандартного виду....

  27. Вправи 525-574 525. АВ = CD; AO : OB = CO : OD; ?СОВ = ?AOD (за двома сторонами і кутом МІНІ ними). З рівності трикутників маємо: BC = AD. ?ВСА = ?DAC. 1) АС – спільна сторона; 2) AB = CD; 3) BC = DA; ∠MCA = ∠MAC; отже, ∠A = ∠C; ?CMА – рівнобедрений; МС […]...

  28. Властивості циліндра 1. 1) В перерізі циліндра площиною трикутник отримати не можна. 2) Прямокутник може бути перерізом циліндра, який проходить через вісі циліндра, або їй паралельний. 3) Трапеція не може бути перерізом циліндра. 4) Квадрат може бути перерізом циліндра, який є рівностороннім. Відповідь: 1) ні; 2) так; 3) ні; 4) так для рівносторонього циліндра. 2. ГМТ, рівновіддалених […]...

  29. Пропорційність відрізків хорд і січних кола Геометрія Кути, пов’язані з колом Пропорційність відрізків хорд і січних кола Теорема 1. Якщо хорди AB і CD кола перетинаються в точці S, то (рисунок 1). Теорема 2. Якщо з точки P до кола проведені дві січні, що перетинають коло відповідно в точках A, B, C, D, то (рисунок 2). Тобто добуток січної, проведеної до […]...

  30. Довжина кола. Число n Урок № 5 6 Тема. Довжина кола. Число n Мета: повторити відомості, які учні мають з початкової школи про коло; сформувати більш строге геометричне уявлення про коло, його елементи та співвідношення між ними; дати зміст поняття “довжина” кола і виробити вміння знаходити довжину кола за відомим радіусом або діаметром та розв’язувати обернену задачу. Тип уроку: […]...

  31. ЕРС. ЗАКОН ОМА ДЛЯ ПОВНОГО КОЛА. З’ЄДНАННЯ ЕЛЕМЕНТІВ – ЗАКОНИ ПОСТІЙНОГО СТРУМУ Фізика підготовка до ЗНО комплексне видання ЕЛЕКТРОДИНАМІКА 2. ЗАКОНИ ПОСТІЙНОГО СТРУМУ 2.4. ЕРС. ЗАКОН ОМА ДЛЯ ПОВНОГО КОЛА. З’ЄДНАННЯ ЕЛЕМЕНТІВ Джерело струму – це пристрій, у якому діють сторонні сили, що розділяють заряди (рис. 22). Рис. 22 Кулонівські сили завжди з’єднують різнойменні заряди. У замкненому колі діють сторонні сили в джерелі й кулонівські сили у […]...

  32. Лабораторна робота № 6 “Дослідження електричного кола з паралельним з’єднанням провідників” 1-й семестр ЕЛЕКТРОМАГНІТНІ ЯВИЩА 2. Електричний струм Урок 17/23 Тема. Лабораторна робота № 6 “Дослідження електричного кола з паралельним з’єднанням провідників” Мета уроку: експериментально перевірити закони паралельного з’єднання провідників. Тип уроку: урок контролю й оцінювання знань. Обладнання: джерело струму, амперметр, вольтметр, ключ, дві електричні лампочки на підставці, з’єднувальні проводи. РЕКОМЕНДАЦІЇ ЩОДО ПРОВЕДЕННЯ ЛАБОРАТОРНОЇ РОБОТИ 1. […]...

  33. Вправи 425-474 425. АС – основа; AB = CB; ∠ADC = 150°. ∠CAD = ∠BAD = x; ∠ACD = 2x; x + 2x + 150° = 180°; 3x = 180° – 150°; 3x = 30°; x = 10°; ∠C = ∠A = 20°; ∠B = 180° – (20° + 20°) = 140°. Відповідь: 20°, 20°, 140°. 426. […]...

  34. Ознаки паралельності двох прямих § 3. Паралельні прямі. Сума кутів трикутника 13. Ознаки паралельності двох прямих Практичні завдання 300. 1) Кути АОМ і CEO – відповідні; 2) кути АОЕ і СЕК – відповідні; 3) кути АОE і OED – різносторонні; 4) кути АОЕ і CEO – односторонні. 1) відповідні; 2) односторонні; 3) різносторонні. 301. 1) ∠1 i ∠5; ∠2 […]...

  35. Лабораторна робота № 6 “Дослідження електричного кола з послідовним з’єднанням провідників” 1-й семестр ЕЛЕКТРОМАГНІТНІ ЯВИЩА 2. Електричний струм Урок 15/21 Тема. Лабораторна робота № 6 “Дослідження електричного кола з послідовним з’єднанням провідників” Мета уроку: експериментально перевірити закони послідовного з’єднання провідників. Тип уроку: урок контролю й оцінювання знань. Обладнання: джерело струму, амперметр, вольтметр, ключ, два резистори, з’єднувальні проводи. РЕКОМЕНДАЦІЇ ЩОДО ПРОВЕДЕННЯ ЛАБОРАТОРНОЇ РОБОТИ 1. Накресліть схему електричного […]...

  36. Властивості тригонометричних функцій УРОК 10 Тема. Властивості тригонометричних функцій Мета уроку: вивчення властивостей тригонометричних функцій у = sin х, у = cos х, у = tg х, у = ctg x (область визначення; область значень; парність (непарність); симетричність графіків; періодичність; нулі; проміжки спадання (зростання); проміжки знакопостійності; найбільші і найменші значення). І. Перевірка домашнього завдання Перевірити правильність побудови графіків […]...

  37. Лабораторна робота № 2 “Дослідження електричного кола з напівпровідниковим діодом” 1-й семестр ЕЛЕКТРОДИНАМІКА 2. Електричний струм УРОК 13/24 Тема. Лабораторна робота № 2 “Дослідження електричного кола з напівпровідниковим діодом” Мета уроку: досліджувати залежність електричного опору кола з напівпровідниковим діодом від напрямку електричного струму. Тип уроку: урок контролю й оцінювання знань. Обладнання: джерело постійного струму, ключ, амперметр, вольтметр, два резистори, сполучні проводи. ХІД РОБОТИ 1. Накресліть […]...

  38. ЕРС. Закон Ома для повного кола 1-й семестр ЕЛЕКТРОДИНАМІКА 2. Електричний струм УРОК 3/14 Тема. ЕРС. Закон Ома для повного кола Мета уроку: розглянути, які потрібні умови для протікання струму в замкнутому колі, й з’ясувати роль джерела струму. Тип уроку: урок вивчення нового матеріалу. ПЛАН УРОКУ Контроль знань 5 хв. 1. Послідовне з’єднання провідників. 2. Паралельне з’єднання провідників. 3. Закон Ома […]...

  39. Властивості піраміди 1. 1) Оскільки піраміда за своїми властивостями має парну кількість ребер, то піраміда не може мати 13 ребер. 2) З’ясуємо, чи має система розв’язки. Розв’язків не має. Отже не існує піраміди, яка має 12 ребер і 6 граней. 2. SABCDEF правильна шестикутна піраміда. AB = BC = CD = DE = EE = AF = […]...

  40. ЗАКОН ОМА ДЛЯ ДІЛЯНКИ КОЛА. ОПІР МЕТАЛЕВИХ ПРОВІДНИКІВ. НАДПРОВІДНІСТЬ – ЗАКОНИ ПОСТІЙНОГО СТРУМУ Фізика підготовка до ЗНО комплексне видання ЕЛЕКТРОДИНАМІКА 2. ЗАКОНИ ПОСТІЙНОГО СТРУМУ 2.2. ЗАКОН ОМА ДЛЯ ДІЛЯНКИ КОЛА. ОПІР МЕТАЛЕВИХ ПРОВІДНИКІВ. НАДПРОВІДНІСТЬ Закон Ома для ділянки кола. Сила струму І в ділянці кола прямо пропорційна прикладеній напрузі U та обернено пропорційна опору провідника R (рис. 16) : Рис. 16 Опір провідника (R) – це властивість провідника […]...

Ви зараз читаєте: Властивості кола. Дотична до кола
«
»