Властивості степеня з натуральним показником
Розділ 1. ЦІЛІ ВИРАЗИ
& 4. Властивості степеня з натуральним показником
Розглянемо властивості степеня з натуральним показником. Вираз а3а2 є добутком двох степенів з однаковими основами. Застосувавши означення степеня, цей добуток можна переписати так:
А3а2 = (ааа) ∙ (аа) = ааааа = а5.
Отже, а3а2 = а5, тобто a5 = а2 + 3. У той самий спосіб неважко перевірити, що х5х4х2 = х5 + 4 + 2 = х11. Тому добуток степенів з однаковими основами дорівнює степеню з тією самою основою і показником, який дорівнює сумі показників множників. Ця властивість справджується
Доведення.
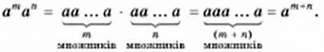
Рівність аmаn = аm+n називають основною властивістю степеня. Вона поширюється на добуток трьох і більше степенів. Наприклад:
Аmаnаk =am + n + k.
З основної властивості степеня випливає правило множення степенів з однаковими основами:
Наприклад, 37 ∙ 35 = 37+5 = 312; 73 ∙ 7 = 73 ∙ 71 = 73+1 = 74; a7a2а3= a7+2+3 =a12.
Оскільки а3а2 = а5, то за означенням частки а5 : а3 = а2, тобто а2 = а5-3. У той самий спосіб неважко пересвідчитися, що х15 : х4 = х11. Тому частка степенів з однаковими основами дорівнює степеню з тією самою основою і показником, який
Доведення. Оскільки аm – n ∙ аn = аm – n + n =аm, тобто аm – n аn =аm, то за означенням частки маємо аm : аn = аm – n.
З доведеної властивості випливає правило ділення степенів.
Наприклад, 318 : 35 = 318 – 5 =313; m9 : m = m9 : m1 = m9 -1 = m8.
Вираз (а7)3 – степінь, основа якого є степенем. Цей вираз можна подати у вигляді степеня з основою а:
(а7)3 = а7 ∙ а7 ∙ а7 = а7 + 7 + 7 = а7∙3 = а21.
У той самий спосіб можна пересвідчитися, що ((х7)3)2 = х42. Тобто степінь при піднесенні до степеня дорівнює степеню з тією самою основою і показником, що дорівнює добутку показників даних степенів.
Доведення.
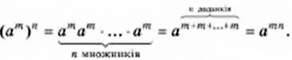
З доведеної властивості випливає правило піднесення степеня до степеня.
Наприклад, (45)4 = 45∙4 = 420; (а8)11 = а8∙11 = а88; ((р3)2)6 = (p3∙2)5 = (p6)5 = p6∙5 = p30.
Вираз (аb)3с степенем добутку множників а і b. Цей вираз можна подати у вигляді добутку степенів а і b:
(ab)3 = аb ∙ ab ∙ ab = (ааа) ∙ (bbb) = a2b3.
Отже, (аb)3 = а3b3.
Таку саму властивість при піднесенні до степеня має будь-який добуток.
Доведення.
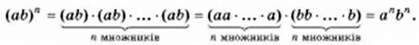
Ця властивість степеня поширюється на степінь добутку трьох і більше множників. Наприклад,
(mpk)n =mnpnkn; (abcd)n = аnbnсndn тощо.
Маємо правило піднесення добутку до степеня.
Наприклад,
(7 ab)2= 72а2b2 = 49 а2b2; (-2хy)3 = (-2)3х3y3 = -8 х3у3.
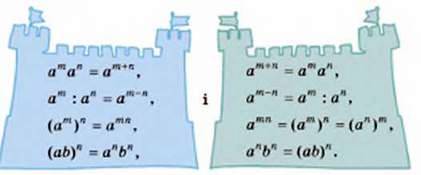
Ліву і праву частини розглянутих тотожностей можна міняти місцями:
Розглянемо, як спростити вирази, що містять степені, та обчислити їх значення.
Приклад 1.
Спростити (а2)3 ∙ (а4а)6.
Р о з в’ я з а н н я.
(а2)3 ∙ (а4а)6 = а6 ∙ (а5)6 = а6а30 =а36.
Приклад 2.
Обчислити:
1) 0,713 : 0,711;
2) 35 ∙ 92 : 272;
3) 27 ∙ 0,58.
Р о з в’ я з а н н я.
1) 0,713 : 0,711 = 0,72 = 0,49.
2) Подамо 92 і 272 у вигляді степеня з основою 3, тобто 92 = (32)2, 272 = (33)2.
Отже, маємо:
35 ∙ 92 : 272 = 35 ∙ (32)2 : (33)2 = З5 ∙ 34 : 36 = 39 : 36 = 33 = 27.
3) Оскільки 0,58 = 0,57 ∙ 0,5, маємо:
27 ∙ 0,58 = 27 ∙ 0,57 ∙ 0,5 = (2 ∙ 0,5)7 ∙ 0,5 = 17 ∙ 0,5 = 1 ∙ 0,5 = 0,5.
Сформулюйте основну властивість степеня. Сформулюйте правила множення степенів, ділення степенів, піднесення степеня до степеня та піднесення добутку до степеня.
95. (Усно) Які з рівностей є правильними:
1) а6 ∙ а2 = а12;
2) а7 а3 = а10;
3) b10 : b5 = b2;
4) b8 : b2 = b6
5) (а7)3 = a21;
6) (а4)5 = а9?
96. (Усно) Подайте добуток у вигляді степеня:
1) m7m4;
2) а9а;
3) 107105;
4) 9 ∙ 95.
97. Запишіть добуток у вигляді степеня:
1) a4а9;
2) c3с10;
3) у5y;
4) 28 ∙ 223.
98. Подайте добуток у вигляді степеня:
1) m3m2;
2) р9р4;
3) 3 ∙ 317;
4) a5а2.
99. (Усно) Представте частку у вигляді степеня:
1) а9 : а2;
2) 715 : 712;
3) b9 : b;
4) 198 : 197.
100. Запишіть частку у вигляді степеня:
1) а7 : а4;
2) х10 : х5;
3) с7 : с;
4) р9 : р8.
101. Подайте частку у вигляді степеня:
1) р9 : р5;
2) х12 : х3;
3) 108 : 10;
4) t12 : t11.
102. (Усно) Запишіть у вигляді степеня:
1)(с7)3;
2) (210)7;
3) (р3)5;
4) (78)11.
103. Подайте у вигляді степеня:
1) (х2)4;
2) (а7)2;
3) (89)3;
4) (103)5.
104. Подайте у вигляді степеня:
1) (m3)4;
2) (Р9)2;
3) (73)10;
4) (192)7.
105. Запишіть вираз x12 у вигляді добутку двох степенів, один з яких дорівнює:
1) х3; 2) х6; 3) х9; 4) х11.
106. Запишіть степінь у вигляді добутку двох степенів з однаковими основами:
1)m7; 2) с12; 3) 517; 4) р8.
107. Подайте добуток у вигляді степеня:
1) (-7)3 ∙ (-7)4 ∙ (-7);
2) aa5a11;
3) bbbb9;
4) (х – у)3(х – у)12;
5) 147 ∙ 145 ∙ 149;
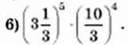
108. Запишіть у вигляді степеня вираз:
1) 123 ∙ 129 ∙ 12;
2) ррр7р;
3) (а + b)3(а + b)5;
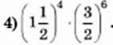
109. Обчисліть значения виразу, використовуючи властивості степенів і таблицю степенів з основами 2 і 3 (див. вправу 71 на с. 20).
1) 23 ∙ 24;
2) 36 : 3;
3) 3 ∙ 33 ∙ 34;
4) 29 : 23.
110. Виконайте піднесення до степеня:
1) (ху)9;
2) (аbс)7;
3) (0,1а)3;
4) (2xу)4;
5) (-2а)5;
6) (- 0,3а)2;
7) (4аb)3;
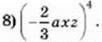
111. Запишіть степінь у вигляді добутку степенів або числа і степенів:
1) (аb)5;
2) (2р)4;
3) (-5аx)3;
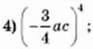
5) (-0,1m)3;
6) (-0,07mx)2.
112. Знайдіть значення виразу:
1) 618 : 616;
2) 0,38 : 0,35;
3) 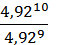
4) 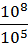 ;
;
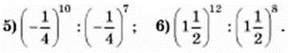
113. Обчисліть:
1)910 : 98;
2)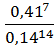
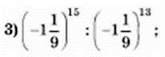
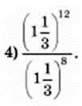
114. Знайдіть значення виразу:
1) 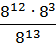 ; 2)
; 2)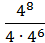 ; 3)
; 3)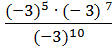 ; 4)
; 4) 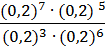
115. Обчисліть:
1) 54 ∙ 512 : 513;
2) 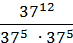 ;
;
3)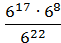 ;
;
4)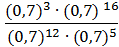
116. Спростіть вираз, використовуючи правила множення і ділення степенів:
1) а7 ∙ а9 : а3;
2) b9 : b5 : b3;
3) m12 : m7 ∙ m;
4) р10 : р9 ∙ р3.
117. Запишіть вираз у вигляді степеня:
1) (a3)4 ∙ а8;
2) ((а7)2)3;
3) (b3)2 : b4;
4) (а4)5 ∙ (а7)2.
118. Подайте вираз у вигляді степеня:
1) (b3)4 ∙ b7;
2) ((х4)5)6;
3) (с3)8 : с10;
4) (m3)6 ∙ (m2)7.
119. Запишіть у вигляді степеня з основою mn:
1) m9n9;
2) m7n7;
3) m2n2;
4) m2015n2015.
120. Подайте у вигляді степеня з основою ab:
1) а5b5;
2) а3b3;
3) а18b18;
4) а2016b2016.
121. Запишіть добуток у вигляді степеня:
1) а4b4;
2) 49a2x2;
3) 0,001a3b3;
4) -8р3;
5)-32а5b5;
6)-а7b7с7;
7) 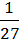 Х3у3;
Х3у3;
8) 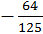 p3q3.
p3q3.
122. Знайдіть таке значення х, при якому рівність є правильною:
1) 35∙ 32=35 + x;
2) 27 ∙ 28 = 21 + х;
3) 4х ∙ 45 = 48;
4) 98 : 9х = 95.
123. Замініть зірочку степенем з основою а так, щоб рівність стала тотожністю:
1) а2 ∙ * = а7; 2)а8 ∙ * = а9; 3) а4 ∙ * ∙ а7 =а19.
124. Замініть зірочку степенем з основою b (b ≠ 0) так, щоб рівність стала тотожністю:
1) b7 : * = b3;
2) * : b5 = b9;
3) b9 : * ∙ b3 = b7;
4) * : b9 ∙ b4 = b10.
125. Знайдіть таке значення х, при якому є правильною рівність:
1) 1,89 : 1,8 = 1,89 – х;
2) 19х : 197 = 199;
3) 412 : 4х = 47.
126. Подайте вираз:
1) 87; (163)5 у вигляді степеня з основою 2;
2) 253; 6257 у вигляді степеня з основою 5.
127. Подайте вираз:
1) 97; (813)5 у вигляді степеня з основою 3;
2) 1004; 10009 у вигляді степеня з основою 10.
128. Обчисліть, використовуючи властивості степенів:
1) 256 : 26;
2) 243 : 34 ∙ 9;
3) 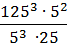 ;
;
4) 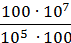
129. Подайте у вигляді степеня (n – натуральне число):
1) x5xn;
2) x8 : хn, n < 8;
3) xn : (х8 ∙ x9), n > 17;
4) х2n : хn ∙ х3n+1;
5) ((x)3)5;
6) (-х4)2n.
130. Знайдіть значення виразу:
1) 53 ∙ 23;
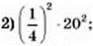
3) 0,213 ∙ 513;
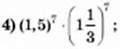
5) 0,57 ∙ 28;
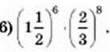
131. Обчисліть:
1) 0,257 ∙ 47;
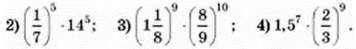
132. Знайдіть значення виразу, використовуючи властивості степенів:
1) 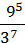 ; 2)
; 2) 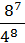 ; 3)
; 3) 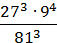 ; 4)
; 4)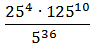 .
.
133. Знайдіть значення виразу:
1) 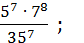 2)
2) 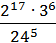 ; 3)
; 3) 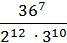 4)
4) 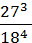
134. Обчисліть:
1) 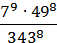 ; 2)
; 2) 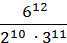 ; 3)
; 3) 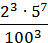 ; 4)
; 4) 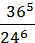
135. Порівняйте вирази:
1) 610 і 365;
2) 1020 і 2010;
3) 514 і 267;
4) 23000 і 32000.
Вправи для повторення
136. Спростіть вираз:
1) 5,2 ∙ 6а;
2) -4,5b ∙ 8;
3) -5х ∙ (-12);
4)  m ∙
m ∙  K;
K;
5)1  x ∙(- 1
x ∙(- 1  y);
y);
6) 1,8а ∙ (-6) ∙ 5с.
137. Вартість деякого товару становила 80 грн. Спочатку її знизили на 15 %, а потім підвищили на 10 %. Знайдіть:
1) вартість товару після зниження;
2) вартість товару після підвищення;
3) як саме і на скільки гривень змінилася вартість товару;
4) як саме і на скільки відсотків змінилася вартість товару.
138. Нехай а + b = 5 і с = -2. Знайдіть значення виразу:
1) а + b – с;
2) а – 2с + b;
3)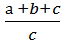 ;
;
4) с(а + b – 4c).
139. Спростіть вираз 1,7 (1  A – 4b) – 1,5(1,2b – а) і знайдіть його значення, якщо а = 5; b =-10.
A – 4b) – 1,5(1,2b – а) і знайдіть його значення, якщо а = 5; b =-10.
Цікаві задачі для учнів неледачих
140. Задача Ньютона. Трава па галявині росте рівномірно щільно й швидко. Відомо, що 70 корів з’їли б її за 24 дні, а 30 корів – за 60 днів. Скільки корів з’їли б усю траву за 96 днів?
цифрами, ділиться на 4.