Вправи 275-324
275. Кут В. а) ВА = ВС, ?АВС – рівнобедрений, у нього дві сторони рівні;
Б) ∠A = ∠C.
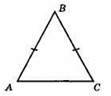
276.
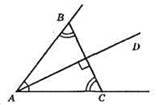
∠A = 60°; AD – бісектриса кута А. BC ⊥ AD; AB = AC; ∠B = ∠C.
277. AB = ВС; АС – основа.
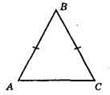
Нехай АВ = ВС = х м, тоді АС = (х + 0,2) м.
Рівняння: х + х + х + 0,2 = 2,6; 3х + 0,2 = 2,6; 3х = 2,4; х = 2,4 : 3; х = 0,8; AB = ВС = 0,8 м; АС = 0,8 + 0,2 = 1 м.
Відповідь: 0,8 м; 0,8 м; 1 м.
278. а) Нехай основа трикутника х см, тоді бічна 7,5 см.
Х + 7,5 + 7,5 = 20; х + 15 = 20; х = 5 (см).
Основа 5 см.
Б) Основа 4 см; бічна х см. х + х +
Бічна сторона 8 см.
В)
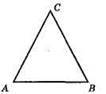
АС : AB = 3 : 4; х – спільна міра відрізків.
АС = ВС = 3х; АВ = 4х.
3х + 3х + 4х = 20; 10х = 20; х = 2.
АС = ВС = 6 см, AB = 8 см.
279. 
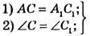за умовою.
AC = BC; A1C1 = B1С1;
3) AC = BC ⇒ A1C1 = B1C1 = BC. ?ABC = ?A1B1C1 за двома сторонами і кутом між ними.
280.
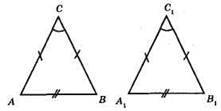
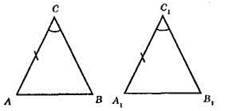
?ABC – рівнобедрений, АС = ВС, ∠A = ∠B; ?A1B1C1 – рівнобедрений, А1С1 = B1C1; ∠A1 = ∠B1.
За умовою маємо: AB = А1В1, ∠A = ∠A1, ∠A = ∠B = ∠A1, ∠A1 = ∠B1, отже, ∠B = ∠B1.
?ABC = ?A1B1C1 за стороною і двома прилеглими кутами (друга
281.
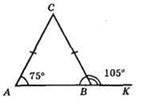
∠CBA – суміжний куту ∠CBK. ∠CBA = 180° – ∠CBK = 180° – 105° = 75°; ∠B = ∠A = 75°; ?ABC – рівнобедрений, AB – основа.
282.
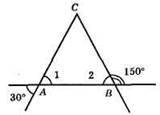
∠1 – вертикальний куту 30°; ∠1 = 30°; ∠2 – суміжний куту 150°; ∠2 = 180° – 150° = 30°; ∠1 = ∠2 = 30°. ?АВС – рівнобедрений, AB – основа.
283.
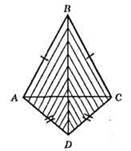
?ABD = ?CBD. З рівності трикутників маємо: АВ = BC, AB = DC.
?ABC – 2 сторони рівні; ?ADC – 2 сторони рівні. ?ABC і? ADC – рівнобедрені трикутники.
284.
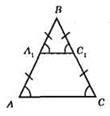
?ABC – рівнобедрений; AB = ВС, ∠A = ∠C. ?А1ВС1 – рівнобедрений, тому що А1В = 1/2AВ; BC1 = 1/2BC, AB = BC, отже, A1B = C1B. У рівнобедреного трикутника кути при основі рівні; ∠A1 =∠C1; ∠BA1C1 = ∠BC1A1.
285.
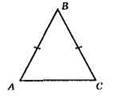
1) Нехай АС = x м, AB = ВС = (x + 3) м.
Рівняння: x + x + 3 + x + 3 = 21; 3x + 6 = 21; 3x = 21 – 6; 3x = 15; x = 15 : 3; x = 5. АС = 5 м, AB = ВС = 8 м.
2) Нехай АВ = ВС = x м, тоді АС = (x + 3) м.
Рівняння: x + x + x + 3 = 21; 3x = 21 – 3; 3x = 18; x = 6. AB = ВС = 6 м, АС = 9 м.
Відповідь: 5 м, 8 м, 8 м або 6 м, 6 м, 9 м.
286. Нехай АС = x см, тоді АВ = ВС = (x + 3) см.
Рівняння: x + x + 3 + x + 3 = 18; 3x + 6 = 18; 3x = 18 – 6; 3x= 12; x = 4; АС = 4 см, AB = ВС = 4 + 3 = 7 (см).
?АDС – рівносторонній, AD = DC = АС = 4 см. Р? ABC = 4 + 4 + 4 = 12 (см).
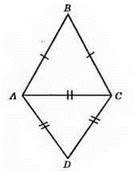
Відповідь: 12 CM.
287.
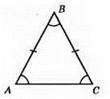
?АВС – рівнобедрений, AB = ВС, ∠A = ∠C, за умовою ∠A = ∠B, ∠C = ∠B. Отже, ∠A = ∠B = ∠C. ?ABC – рівносторонній.
288.
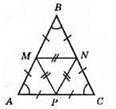
?ABC – рівносторонній, AB = ВС = AC, ∠A = ∠B = ∠C, AM = MB, BN = NC, AP = PC. ?AMP = ?BMN = ?CNP (за першою ознакою рівності трикутників). З рівності трикутників маємо: MN = NP = МР, отже, ?MNP – рівносторонній.
289.
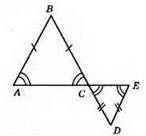
AB = ВС, CD = DE. ?ABC – рівнобедрений. Кути при основі рівні: ∠BAC = ∠BCA. ?CDE – рівнобедрений, кути при основі рівні: ∠DEC = ∠DCE.
∠DCE = ∠ACB (вертикальні кути). Отже, ∠BAC = ∠DEC.
290.
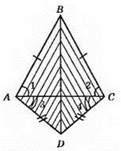
AB = BC, AD = DC – за умовою. ∠BAC = ∠BCA; ∠CAD = ∠DCA; ∠A = ∠1 + ∠3; ∠C = ∠2 + ∠4; ∠A = ∠C. ?ABD = ?CBD за двома сторонами і кутом між ними.
291.
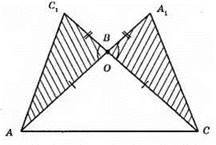
А) AB = ВС; BA1= ВС1; ?С1ВА = ?A1ВС.
1) ВС1 = ВА1; 2) AB = ВС; 3) ∠C1BA = ∠A1BC – вертикальні кути.
Трикутники рівні за першою ознакою рівності трикутників.
Б) ?AС1С = ?СА1A.
1) С1С = С1В + ВС; А1А = А1В + АВ ⇒ С1С = А1А; 3) ∠C1CA = ∠A1AC; 3) АС – спільна сторона.
?AС1С = ?СА1А за двома сторонами і кутом між ними.
292.
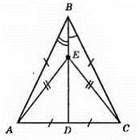
?АВС – рівнобедрений, АС – основа, AB = BC, AD = DC.
Доведемо, що? АЕС – рівнобедрений.
1) ?ABD = ?CBD; ∠ABD = ∠CBD;
2) ?АВЕ = ?СВЕ; АВ = ВС; BE – спільна сторона, ∠ABE = ∠CBE;
3) з рівності? АВЕ і? СВЕ маємо: АЕ = ЕС, отже, ?АЕС – рівнобедрений.
293.
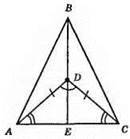
1) ∠ADE = ∠CDE; ∠DAE = ∠DCE; AD = DC;
2) ?ABD = ?CBD; 1) BD – спільна; 2) AD = DC; 3) ∠BDA = ∠BDC – суміжні кути до рівних кутів. З рівності? ABD і? CBD: AB = ВС. Отже, ?ABC – рівнобедреник.
294. а) Якщо сума кутів 180°, то вони суміжні (неправильне твердження).
Б) Якщо прямі паралельні одна одній, то вони паралельні третій (неправильне твердження).
В) Якщо трикутники рівні, то у них рівні дві сторони і кут між ними (правильне твердження).
296.
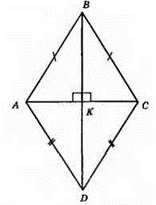
?ABC – рівнобедрений, AB = ВС; ?АВК = ?СВК. З рівності? ABD і? CBD: ∠САКВ і ∠CKB – рівні суміжні кути; ∠САКВ = ∠CKB = 90°; AK = КС, точка К – середина відрізка АС.
297.
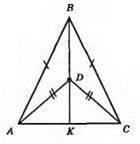
?ВАК = ?ВСК, ?АВС – рівнобедрений, AB = ВС; ∠DAK = ∠DCK, ?ADC – рівнобедрений. ?ABD = ?CBD (AB = ВС, AD = DC, ∠BAD = ∠BCD). З їх рівності: ∠ABK = ∠CBK. ?АВК = ?СВК (AB = ВС, ∠A= ∠C, ∠ABK = ∠CBK). З їхньої рівності: ∠AKB = ∠CKB, в це суміжні кути, отже, вони рівні, ВК ⊥ АС, ∠AKB = ∠CKB = 90°. .
298.
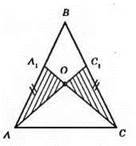
?ABC – рівнобедрений. АА1 = СС1, АВ = ВС; АС1 і СА1 перетинаються в т. О. AA1 = СС1; ?АА1С = ?СС1А; АС – спільна; ∠A = ∠C; AA1 = CC1.
?АА1O = ?СС1O; ∠AA1O = ∠CC1O; А1А = С1С; ∠A1AO = ∠C1CO.
З рівності цих трикутників: АО = ОС, отже, ?АОС – рівнобедрений, AO = СО.
299.
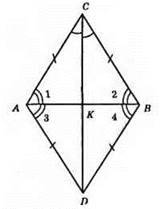
?ABC = ?ABD. З їх рівності: 1) АС = AD; 2) ВС = BD; 3) ∠A = ∠1 + ∠3, ∠B = ∠2 + ∠4, ∠1 = ∠2, ∠3 = ∠4.
?CAD = ?CBD (за першою ознакою). З їх рівності: ∠ACK = ∠BCK. ?АСК = ?ВСК (АС = ВС, СК – спільна, ∠ACK = ∠BCK). Отже, ∠АКС = ∠BKC, а це суміжні кути, ∠AKB = ∠BKC = 90°, CK ⊥ AB, CD ⊥AB.
300. AD ⊥ OB, ∠AOB – гострий.
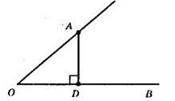
Точка О не лежить між точками В і D.
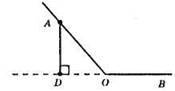
∠AOB – тупий, AD ⊥ OB. Точка О лежить між точками B i D.
301.
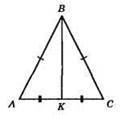
Відрізок BD ділить рівнобедрений? ABC на 2 рівні трикутники? АВК i? CBK. BK ⊥ AC, AK = KC, ∠ABK = ∠CBK.
302.
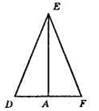
А) DA = AF, ЕА – медіана;
Б) ∠DAE = ∠FAE, ЕА – висота;
В) ∠DEA = ∠FEA, ЕА – бісектриса;
Г) DE = EF, DA = AF, медіана, висота, бісектриса.
303. Якщо трикутник тупокутний, всередині лежить тільки одна висота.
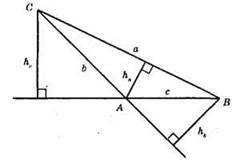
Тільки дві висоти не можуть лежати в трикутнику.
304. Не може.
305.
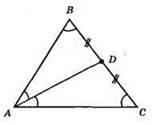
AD – медіана, висота, бісектриса; AB = ВС; ∠ABC = ∠ACD.
306.
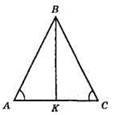
∠A = ∠C. Бісектриса ∠B.
307. У рівнобедреному трикутнику проведено всі медіани, висоти, бісектриси. До бічних сторін по 3 відрізки, до основи 1 відрізок. Всього 7 відрізків.
У рівносторонньому трикутнику проведено всі висоти, медіани, бісектриси. Всього 3 відрізки.
308.
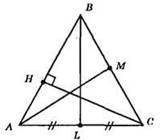
А) ВМ = MC, AM – медіана;
Б) BL – медіана, висота, бісектриса;
В) СН – висота? ABC.
309.
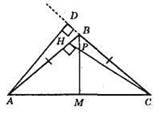
?ABC; ∠B – тупий кут.
А) AD – висота до сторони ВС. Точка D не лежить на відрізку ВС.
Б) ВМ – медіана. ∠ABM = ∠CBM.
В) CH ⊥ AB, СН – висота.
310.
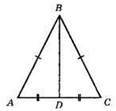
AB = ВС; ?ABC – рівнобедрений, AD = DC, BD – медіана.
P? ABD = 12 CM; BD = 4 см. P? ABC =АВ + ВС + АС; Р? ABD = АВ + AD + BD; AB + AD = Р? ABD – BD = 12 – 4 = 8 (см). Р? ABC = 2(AB + AD) = 2 x 8 = 16 (CM).
Відповідь: 16 см.
311.
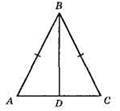
?АВС – рівнобедрений. AB = ВС; AD = DC. Р? ABC = 18 см; BD = 5 см. Р? ABD = (АВ + AD) + BD; Р? ABC = (AB + AD) + (BC + DC); AB + AD = Р? ABC : 2; AB + AD = 18 : 2 = 9 (см). Р? ABD = 9 + 5 = 14 (CM).
Відповідь: 14 см.
312.
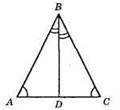
?ABC; ∠A = ∠C, BD – бісектриса кута В. Якщо ∠A = ∠C, то? ABC – рівнобедрений, отже, BD є медіаною, тому AD = CD.
313.
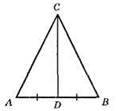
CD – медіана; AD = BD. CD – висота; CD ⊥ AB; ∠ADC = ∠BDC = 90°; ?ACD = ?BCD. 1) CD – спільна сторона; 2) AD = BD; 3) ∠CDA = ∠CDB. Трикутники рівні за першою ознакою рівності трикутників. Отже, ∠A = ∠B.
314.
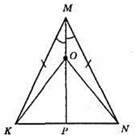
?KMN – рівнобедрений, KN – основа, МР – висота.
МР – висота і бісектриса, ∠KMO = ∠NMO; ?КМО = ?NMO. 1) KM = MN; 2) МО – спільна сторона; 3) ∠KMO = ∠NMO. Трикутники рівні за першою ознакою. З їхньої рівності маємо: OK = ON. ?KON – рівнобедрений.
315.
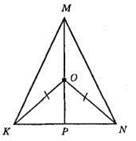
?KON – рівнобедрений, OK = ON; OP – бісектриса; ∠KOP = ∠NOP; ?MOK = ?MON; 1) ОМ – спільна сторона; 2) OK = ON; 3) ∠MOK = ∠MON, кути суміжні рівним кутам ∠KOP і ∠NOP. З рівності трикутників маємо: КМ = NM, ?KMN – рівнобедрений.
316.
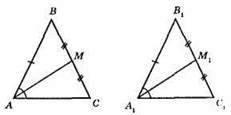
?ABC = ?A1B1C1; AM i А1М1 – медіани рівних трикутників.
?AMВ = ?А1М1В1 (за першою ознакою).
1) AB = A1B1; 2) BM = B1M1; 3) ∠B = ∠B1. З рівності трикутників маємо: AM = A1M1.
317.
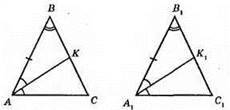
?ABC = ?A1B1C1; AK і A1K1 – медіани трикутників.
?ABK = ?A1B1K1. 1) AB = A1B1; 2) ∠B = ∠B1; 3) ∠BAK = ∠B1A1K1.
?ABK = ?A1B1K1 за другою ознакою рівності трикутників. З рівності трикутників маємо: AK = A1K1.
318.
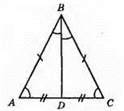
P? ABC = 28 см; P? ABC = 20 см; AB = BC; BD – бісектриса, медіана, висота. AD = DC.
(AB + AD) + (DC + BC) = 28 см; AB + AD = 14 cм; (AD + AD) + BD = 20 (cм). 14 + BD = 20; BD = 20 – 14; BD = 6 CM.
Відповідь: 6 см.
319.
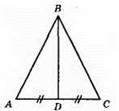
?АBС; BD – медіана; P? ABC = AB + BC + АС; AC = AD + DC; AB + AD = BC + DC, D – середина AC; AD = DC, тобто у рівності AB + AD = BC + DC; AB = DC; ?ABC – рівнобедрений.
320.
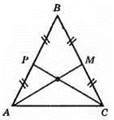
?ABC – рівнобедрений; СР і AM – медіани. ?ABM = ?СВР (за першою ознакою).
1) AB = CD; 2) PB = MB; 3) ∠B – спільний. З їх рівності маємо: AM = СР.
321.
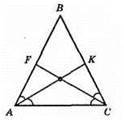
?ABC – рівнобедрений; АК і CF – бісектриси; ?AFC = ?СКА. 1) АС – спільна сторона; 2) ∠A = ∠C; 3) ∠FCA = ∠KAC (АК і CF – бісектриси).
?AFC = ?АСК за стороною і двома прилеглими кутами. Отже, AK = CF.
322.
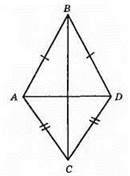
?ABC = ?DBC. Доведемо, що AO = OD.
З їхньої рівності маємо: ∠ABO = ∠DBO, OB – бісектриса у рівнобедреному AABD, а отже, OB і медіана, тому AO = OD.
323.
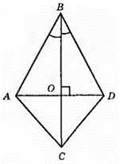
AD ⊥ BC; ∠ABC = ∠DBC. Доведемо, що? ACD – рівнобедрений. ?АОВ = ?DOB.
1) OB – спільна сторона;
2) ∠ABO = ∠DBO; 3) ∠BOA = ∠BOD = 90°, AD ⊥ BC. З рівності трикутників маємо: AO = OD. ?АОС = ?DOC. 1) AO = OD; 2) OC – спільна сторона; 3) ∠AOC = ∠DOC = 90°. З рівності трикутників маємо: АС = DC. Тобто? ACD – рівнобедрений.
324.
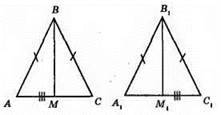
Дано: ?ABC і? A1B1C1; AB = BC; A1B1 = B1C1; AC = A1C1; BM = B1M1.
В рівнобедреному трикутнику медіана є висотою, отже ∠AMB = ∠CMB = 90°.
1) ∠A1M1B1 = ∠C1M1B1 = 90°; 2) BM = B1M1; 3) AM = A1M1.
?АВМ = ?А1В1М1, отже, AB = А1В1, ∠A = ∠A,.
?ABC = ?A1B1C1. 1) AC = A1C1; 2) ∠A = ∠A1; 3) AB = A1B1.
(1 votes, average: 5.00 out of 5)
Loading...