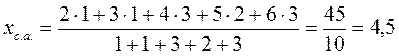Характеристики варіаційних рядів. Середні величини. Мода, медіана вибірки
УРОК № 46
Тема. Характеристики варіаційних рядів. Середні величини. Мода, медіана вибірки
Мета уроку: домогтися засвоєння учнями змісту понять: середнє значення, мода вибірки, медіана вибірки. Закріпити знання учнів про зміст понять, вивчених на попередньому уроці. Працювати над формуванням умінь пояснювати зміст вивчених понять, наводити приклади, що ілюструють ці поняття, а також розв’язувати задачі, що передбачають відшукання середніх значень величин, моди та медіани вибірки.
Тип уроку: засвоєння знань, вироблення вмінь.
Наочність
Хід уроку
I. Організаційний етап
Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.
II. Перевірка домашнього завдання
Учитель організує роботу учнів з перевірки домашнього завдання за зразком.
III. Формулювання мети і завдань уроку.
Мотивація навчальної діяльності учнів
Учитель повідомляє учнів про те, що варіаційні ряди характеризуються не тільки частотою та відносною частою, а й іншими параметрами. Метою даного уроку є вивчення питання про види цих параметрів, їхній зміст та спосіб обчислення.
IV. Актуалізація опорних
Усні вправи
1. Обчисліть значення виразу:
1) | -0,6 ? (-0,3) | 2) | (3,1 + 0,09)0 |
-0,2 | : | ||
Х10 | -1,5 | ||
:5 | :0,5 | ||
? | ? |
2. Спростіть вираз:
1) (а2)9 : а3;
2) (x + 2)(х – 6);
3) 4,9а5 ? 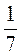 А;
А;
4) 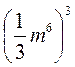 ;
;
5) (3а + 5) – (2 – а);
6) 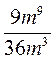 .
.
3. Для вибірки 1; 1; 3; 3; 3; 5; 8; 8 укажіть: варіанти; варіаційний ряд; частоти; відносні частоти; об’єм.
V. Формування знань
План вивчення нового матеріалу
1. Середні значення. Обчислення середнього арифметичного величини.
2. Мода вибірки.
3. Медіана вибірки.
4. Приклади розв’язування задач.
Опорний конспект № 27
Вибірки характеризуються центральними тенденціями: середнім значенням, модою і медіаною |
Середнє арифметичне значення
|
Зважене середнє арифметичне значення
|
Мода вибірки – це значення ознаки, яка найбільш часто повторюється у вибірці. |
Медіаною вибірки називається варіанта, яка розміщена посередині варіаційного ряду. |
Приклад. Дано вибірку вимірювання повітря температури (t, °С) у першу декаду квітня: 5; 6; 4; 3; 4; 5; 6; 2; 4; 6. Складіть статистичний ряд; визначте варіанти та їхні частоти; складіть варіаційний ряд, для якого знайдіть середнє зважене значення, моду та медіану. |
Розв’язання Статистичний ряд даної вибірки: 2, 3, 4, 4, 4, 5, 5, 6, 6, 6. Варіанти, варіаційний ряд: 2, 3, 4, 5, 6; частоти відповідно дорівнюють 1, 1, 3, 2, 3. |
Середнє зважене значення:
|
Мода дорівнює 4 і 6, бо 4 і 6 повторюються найчастіше – по 3 рази. |
Оскільки у варіаційному ряді 5 чисел: 2, 3, 4, 5, 6, то медіана дорівнює 4. |
Методичний коментар
Вивчення матеріалу уроку починається з формування загального уявлення учнів про існування різних видів характеристик варіаційних рядів. Після цього послідовно формуються знання про зміст понять: середнє арифметичне та зважене середнє арифметичне значення, мода та медіана вибірки. Так само, як і на попередньому уроці, наголошуємо на тому, що згідно з програмовими вимогами учні мають лише описувати поняття середнього значення, а також розв’язувати задачі на знаходження середніх значень та моди і медіани вибірки. Тому після формулювання означень названих понять приділяємо увагу закріпленню змісту та виробленню схеми дій при розв’язуванні задач на відшукання названих величин, розв’язавши якомога більше задач на обробку статистичних даних із різних галузей науки і техніки.
VI. Формування вмінь
Усні вправи
1. Знайдіть середнє арифметичне значення за таблицею:
Крамниця | Порядковий номер крамниці | ||||
1 | 2 | 3 | 4 | 5 | |
Площа крамниці, м2 | 50 | 60 | 90 | 70 | 70 |
2. Знайдіть моду за даною таблицею статистичного розподілу:
Розмір чоловічого взуття | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 |
Кількість проданих пар | – | 7 | 8 | 19 | 28 | 25 | 10 | 1 |
Що показує мода в даному випадку?
3. Стаж роботи п’яти робітників становить: 4, 5, 8, 9, 11 років. Знайдіть медіану цієї вибірки.
4. Стаж роботи шести робітників становить: 7, 8, 9, 10, 12, 14 років. Знайдіть медіану цієї вибірки.
Письмові вправи
Для реалізації дидактичної мети уроку слід розв’язати вправи такого змісту:
1) обчислити середнє арифметичне та зважене середнє арифметичне значення для статистичних даних;
2) знайти моду та медіану варіаційної вибірки;
3) на повторення: задачі на застосування понять, вивчених на попередньому уроці, та на побудову полігона частот і гістограми.
VII. Підсумки уроку
Контрольні запитання
1. Запишіть формулу для обчислення простого середнього арифметичного. Наведіть приклади.
2. Запишіть формулу для обчислення зваженого середнього арифметичного. Наведіть приклади.
3. Що таке мода? Що показує мода? Наведіть приклади.
4. Що таке медіана? Наведіть приклад.
VIII. Домашнє завдання
1. Вивчити означення понять, розглянутих на уроці, навести свої власні приклади до вивчених понять і записати їх у зошит.
2. Виконати самостійну роботу (див. нижче) за варіантом, указаним учителем.
3. Повторити: основні поняття теми 3 (див. опорні конспекти № 23-27), поняття середнього арифметичного даних чисел.
Самостійна робота
Варіант 1
Знайдіть центральні тенденції, складіть частотну таблицю вибірки та побудуйте відповідну гістограму:
1) для вибірки 2, 3, 3, 5, 6, 6, 6, 7, 9;
2) для вибірки 1, 5, 7, 3, 7, 1, 7, 8, 3, 2;
3) якщо в таблиці подано відомості про вік 20 дітей, які прийшли на сеанс до кінотеатру:
12 | 14 | 15 | 12 | 16 |
13 | 14 | 16 | 15 | 14 |
14 | 15 | 15 | 16 | 14 |
12 | 13 | 15 | 16 | 14 |
4) для статистичного дослідження успішності складання учнями 9 класів ДПА з алгебри, якщо вони отримали такі бали: 7, 7, 9, 12, 4, 5, 11, 11, 12, 9, 9, 9, 10, 10, 7, 9, 9, 8, 4, 5, 8, 8, 8, 9, 10, 11, 7, 6, 9, 5, 5, 12, 9, 10, 10, 7, 9, 12, 4, 5, 11, 7, 8, 9, 10, 11, 7, 6, 9, 8, 10, 7, 9, 12, 4, 9, 8, 10, 10, 12, 11, 12, 9, 10, 7, 7, 4, 7.
Варіант 2
Знайдіть центральні тенденції, складіть частотну таблицю вибірки та побудуйте відповідну гістограму:
1) для вибірки 1, 3, 3, 4, 4, 4, 6, 6, 7;
2) для вибірки 11, 15, 17, 16, 16, 13, 15, 14, 13, 15, 12;
3) якщо в таблиці подано відомості про помилки під час тестування 25 дітей:
2 | 1 | 2 | 2 | 0 |
3 | 4 | 0 | 1 | 5 |
0 | 1 | 2 | 2 | 4 |
4 | 3 | 0 | 2 | 2 |
3 | 3 | 3 | 1 | 2 |
4) для статистичного дослідження успішності складання учнями 9 класів ДПА з алгебри, якщо вони отримали такі бали: 6, 7, 9, 12, 4, 5, 12, 9, 9, 8, 10, 10, 7, 9, 9, 8, 4, 5, 6, 8, 8, 9, 10, 5, 7, 6, 9, 5, 5, 7, 9, 10, 10, 7, 9, 12, 4, 5, 8, 7, 8, 9, 10, 11, 7, 6, 10, 7, 9, 11, 4, 9, 8, 10, 10, 12, 11, 12, 9, 10, 7, 7, 4, 3.
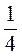
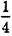
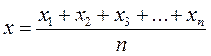 , де xi – значення ознаки (варіанти); n – число одиниць сукупності; де x – середнє арифметичне значень xi ознаки.
, де xi – значення ознаки (варіанти); n – число одиниць сукупності; де x – середнє арифметичне значень xi ознаки.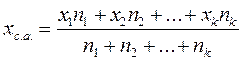 , де хi – варіанти; nі – частоти.
, де хi – варіанти; nі – частоти.