Застосування модуля числа. Відстань між точками на координатній прямій
Урок № 6 7
Тема. Застосування модуля числа. Відстань між точками на координатній прямій
Мета: поглибити знання учнів про властивості модуля раціонального числа та відпрацювати навички застосування означення та властивостей модуля для розв’язування рівнянь та нерівностей.
Тип уроку: застосування знань, умінь і навичок
Хід уроку
I. Перевірка домашнього завдання
Математичний диктант
Варіант 1 [2]
1. Запишіть рівність: модуль числа -5 дорівнює 5. [Модуль числа 7 дорівнює 7.] Чи правильна ця рівність?
2. Чому дорівнює
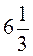
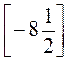 ?
?3. Чому дорівнює модуль числа 0 [9]?
4. Чому дорівнює модуль числа -3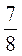 [0] ?
[0] ?
5. Модуль числа х [у] дорівнює 4,1 [8,2]. Чому дорівнює модуль числа, протилежного до х [у]?
6. Розв’яжіть рівняння | х | = 3 [| y | = 4].
II. Актуалізація опорних знань
Бесіда. Запитання до класу
– Що називають модулем числа?
– Як позначають модуль?
– Чому дорівнює модуль додатного числа? нуля?
– Чому дорівнює модуль від’ємного числа?
– Чи може модуль якого-небудь числа бути від’ємним числом?
– Чи правда, що якщо модулі
Точка А належить відрізку MN. Виразіть:
A) MN через МА і AN; б) МА через MN та AN;
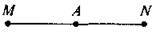
В) AN через MN та AM.
III. Поглиблення знань
1. Мотивація навчальної діяльності
Слово вчителя
@ Ми знаємо, що таке модуль числа, як знайти модуль різних раціональних чисел та як розв’язати рівняння вигляду | х | = а, а – невід’ємне число. Виникає запитання, а чи є завдання, де можна застосувати поняття модуля?
2. Відстань між двома точками на координатній прямій
А) 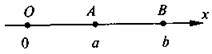
Нехай дано А(а) і B(b) і нехай b > а додатні; тоді АВ = ОВ – ОА = b – а = |b| – |а|.
Наприклад, якщо A(5,3); В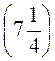 ,то АВ = 7
,то АВ = 7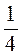 – 5,3 = 7,25 – 5,30 = 1,95 (од. відр.)
– 5,3 = 7,25 – 5,30 = 1,95 (од. відр.)
Б)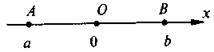
Нехай дано А(а) і B(b), причому а – від’ємне, b – додатне. Тоді АВ = AO + OB = |a| + |b|.
Наприклад, якщо А (-5,3), В 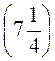 , то АВ = |-5,3| +
, то АВ = |-5,3| +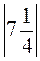 = 5,3 + 7,25 = 12,25 (од. відр.)
= 5,3 + 7,25 = 12,25 (од. відр.)
В)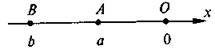
Нехай дано А(а) і B(b), причому а і b – від’ємні, тоді якщо а ближче до О (|a| < |b|), то AB = |a| – |b|.
Якщо ж а далі від 0, ніж b, то AB = |b| – |а|.
Наприклад, A(-5,3), В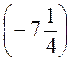 , тоді оскільки |-5,3| <
, тоді оскільки |-5,3| < 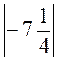 , то АВ=
, то АВ= 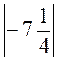 – |-5,3| = 7
– |-5,3| = 7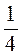 – 5,3 = 1,95 (од. відр.).
– 5,3 = 1,95 (од. відр.).
3. Розв’язування нерівностей з модулем
Ми знаємо, що |х| = а, якщо а – додатне, має два розв’язки: а і – а.
Як розв’язати нерівність |х| < а, а – додатне. Зрозуміло, що за означенням модуля цю нерівність задовольняють усі числа, відстань від яких до точки О(0) менша за а. Можна здогадатися, що таких чисел (ближчих до 0, ніж до а безліч, і всі вони лежать між точками з координатами а та – а (див. рис.)).
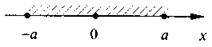
Тобто – а < х < а.
Наприклад. Розв’яжіть нерівність |х| < 3.
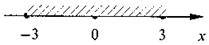
-3 < х < 3.
4. Висновок
Означення і властивості модуля ми використовуємо для:
А) знаходження модуля числа;
Б) розв’язування рівнянь |х| = а;
В) розв’язування нерівностей |х| < a;
Г) знаходження відстані між двома точками на координатній прямій.
IV. Відпрацювання навичок
Письмові вправи
1. Скільки існує цілих чисел, які задовольняють нерівність |х| < 5? Позначте їх на координатній прямій.
2. Позначте на координатній прямій множину всіх значень х, які задовольняють нерівність | x | < 0,5.
3. Скільки існує натуральних чисел, які задовольняють нерівність |х| < 12? Скільки цілих від’ємних чисел? Скільки цілих чисел?
4. Знайдіть відстань між точками А і В на координатній прямій, якщо:
А) A(3,4) і B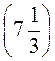 ; б) А(-0,14) і В(-5,03); в) A
; б) А(-0,14) і В(-5,03); в) A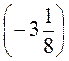 i В
i В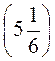 .
.
5. З двох чисел оберіть те, в якого модуль більше:
А) -5,87 та -7,82; б) 2,75 та 0; в) -700,1 та 0,24; г) -2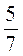 та 3
та 3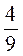 ; д) –
; д) –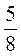 та
та 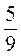 ; є) –
; є) –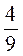 та –
та –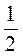 .
.
6. Де на координатній прямій може лежати точка, яка відповідає х, якщо а) |х| = 3; б) |х| < 3; в) |х| > 3?
Додатково (на повторення)
7. Серед чисел -(-7); -3; 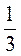 ; -7; 3; –
; -7; 3; –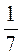 ; –
; –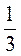 ;
; 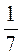 випишіть пари: а) протилежних чисел; б) обернених чисел.
випишіть пари: а) протилежних чисел; б) обернених чисел.
8. Ніна витратила в магазині 4,8 грн. Скільки грошей витратила Оля, якщо відомо, що Ніна витратила:
А) на 0,3 грн більше за Олю;
Б) на 0,5 грн менше від Олі;
В) у 2 рази більше за Олю;
Г) у 1,5 рази менше від Олі;
Д) 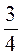 того, що витратила Оля;
того, що витратила Оля;
Є) 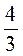 того, що витратила Оля;
того, що витратила Оля;
Ж) 0,2 того, що витратила Оля;
З) 25 % того, що витратила Оля;
К) на 25 % більше того, що витратила Оля;
Л) 125 % того, що витратила Оля?
V. Підсумки уроку
Ігровий момент
Тестові запитання
На дошці записано ціле від’ємне число, наприклад -19. Учні (або 1 учень-експерт) повинні швидко відповісти на запитання, які вчитель ставить у короткій формі:
1) Яке це число?
2) Його модуль?
3) Йому протилежне?
4) Йому обернене?
5) Де розташовано на координатній прямій?
6) Відстань від початку відліку?
7) Відстань між ним і йому протилежним?
8) Число, що має менший модуль.
VI. Домашнє завдання
1. З двох чисел оберіть те, яке має менший модуль:
А) – 45,1 та 8,31; б) – 45,3 та 57,8; в) 76,9 та -57,1; г) -13,8 та -13,7; д) -2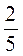 та 3
та 3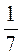 ; є) 2
; є) 2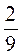 та -5
та -5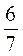 ; ж) –
; ж) –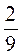 та
та 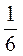 ; з)
; з) 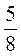 та –
та –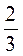 .
.
2. Знайдіть цілі значення х, які задовольняють нерівність: a) |х| < 6; б) |х| < 4,8; в) *8 > |y|.
3. Яка відстань між точками С(-20,3) і D(-3,75) на координатній прямій?
4. Знаючи, що а, b, с – додатні числа, а х, у, z – від’ємні числа, допишіть рівності: а) |а| = …; б) |-b| = …; в) |с| = …; г) |х| = …; д) |у| = ..:, е) |-z| = ….
5. Знайдіть значення виразу 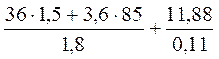 .
.