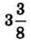ЗНАХОДЖЕННЯ ЧИСЛА ЗА ЙОГО ДРОБОМ
Цілі:
– навчальна: удосконалити вміння виконувати вправи, у яких передбачено знаходження числа за його дробом; узагальнити та систематизувати знання учнів з теми “Звичайні дроби”;
– розвивальна: формувати вміння аналізувати інформацію, узагальнювати та робити висновки;
– виховна: виховувати відповідальність за результати своєї роботи, свідоме ставлення до навчання;
Тип уроку: комбінований.
Обладнання та наочність:
Хід уроку
І. ОРГАНІЗАЦІЙНИЙ ЕТАП
____________________________________________
____________________________________________
____________________________________________
II.
1. Перевірка завдання, заданого за підручником
____________________________________________
____________________________________________
2. Самостійна робота з подальшою самоперевіркою за готовими розв’язаннями
Варіант 1
1) Турист подолав 2/3 маршруту. Яка довжина маршруту, якщо він пройшов 4 км?
2) Частину огірків, що принесли з городу, засолили, а 12 кг залишили свіжими. Скільки кілограмів огірків засолили, якщо свіжими залишили 2/7 усіх огірків, принесених із городу?
Варіант 2
1) Велосипедист подолав 5/8 дороги. Яка довжина дороги, якщо він проїхав 40 км?
2) Частину
III. УДОСКОНАЛЕННЯ ВМІНЬ І НАВИЧОК
1. Робота за підручником (§ 25)
Письмово: № 993, 994, 995, 997.
2. Додаткове завдання
Заповніть порожні комірки в таблиці.
Число а | 12 | 60 |
2/3 від а | 16 | 88 |
3/4 від а | 27 | 135 |
IV. УЗАГАЛЬНЕННЯ ТА СИСТЕМАТИЗАЦІЯ ЗНАНЬ Фронтальне опитування
1. Наведіть приклади звичайних дробів. Що показує чисельник і знаменник дробу?
2. Сформулюйте правила порівняння дробів з однаковими знаменниками.
3. Який дріб називають правильним? неправильним? Який із цих дробів більший за одиницю, який дорівнює одиниці і який менший від одиниці? Наведіть приклади.
4. Як неправильний дріб перетворити на мішане число? Поясніть на прикладі дробів 14/5, 103/10.
5. Як записати у вигляді неправильного дробу:
1) натуральне число; 2) мішане число? Наведіть приклади.
6. Сформулюйте правило знаходження дробу від числа. Наведіть приклади.
7. Сформулюйте правило знаходження числа за його дробом. Наведіть приклади.
V. ПІДСУМКИ УРОКУ
1.
____________________________________________
____________________________________________
2. Виконання тестових завдань
Обведіть кружечком букву, яка, на вашу думку, відповідає правильній відповіді.
Варіант 1 | Варіант 2 | ||||||
1. Яке з наведених чисел найбільше? | 1. Яке з наведених чисел найбільше? | ||||||
А | Б | В | Г | А | Б | В | Г |
4 |
| 33/8 | 4/4 | 5 | 34/11 | 28/28 | 35/6 |
2. Чому дорівнює х, якщо х:4 від 12 дорівнює 9? | 2. Чому дорівнює у, якщо у:5 від 15 дорівнює 12? | ||||||
А | Б | В | Г | А | Б | В | Г |
3 | 16 | 8 | 6 | 9 | 5 | 4 | 10 |
Відповіді
Варіант 1 | 1-В, 2-А |
Варіант 2 | 1-Г, 2-В |
VI. ДОМАШНЄ ЗАВДАННЯ
1. Завдання за підручником: § 25, № 996, 998.
На повторення. Тестові завдання (с. 223).
2. Додаткове завдання. Знайдіть 3/4 від числа а, якщо 7/8 числа а становлять 21.
Відповідь. 18.