Головна ⇒ 📌Математика ⇒ ЗВЕДЕННЯ ДРОБІВ ДО СПІЛЬНОГО ЗНАМЕННИКА. ПОРІВНЯННЯ ДРОБІВ

ЗВЕДЕННЯ ДРОБІВ ДО СПІЛЬНОГО ЗНАМЕННИКА. ПОРІВНЯННЯ ДРОБІВ

Розділ 2 ЗВИЧАЙНІ ДРОБИ ТА ДІЇ З НИМИ

§ 7. ЗВЕДЕННЯ ДРОБІВ ДО СПІЛЬНОГО ЗНАМЕННИКА. ПОРІВНЯННЯ ДРОБІВ

Ви вже знаєте, що дріб 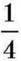можна замінити дробом 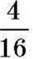тому, що значення цих дробів рівні: 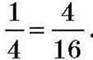Про таку рівність кажуть, що дріб 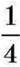звели до нового знаменника 16.

Під час зведення дробу до нового знаменника застосовують основну властивість дробу.

Часто наперед відомо, до якого саме знаменника треба звести даний дріб. Наприклад, дріб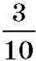

class=""/> треба звести до знаменника 50. Для цього спочатку слід дізнатись, у скільки разів новий знаменник. 50 більший за знаменник даного дробу: 50: 10=5 (разів). Потім – у стільки ж разів треба збільшити чисельник даного дробу:

3 ∙ 5 = 15. Отже,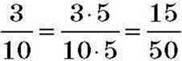

Число 5 називають додатковим множником.

Зверніть увагу:

– додатковий множник є натуральним числом;

– щоб знайти додатковий множник, поділіть новий знаменник на знаменник даного дробу.

Чи до будь-якого знаменника можна звести даний дріб? Ні. Наприклад, дріб 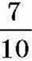знаменника 11 або 25, оскільки ані число 11, ані

число 25 не ділиться на число 10.

Запам’ятайте!

Правило зведення дробу до нового знаменника

Щоб звести дріб до нового знаменника, треба:

1) записати новий знаменник у знаменнику нового дробу;

2) визначити додатковий множник як частку нового знаменника і знаменника даного дробу;

3) помножити чисельник даного дробу на додатковий множник і результат записати в чисельнику нового дробу.

Наприклад:

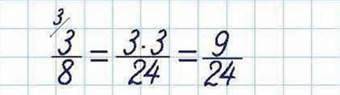
Якщо дроби звели до нових знаменників і їх знаменники дорівнюють один одному, то кажуть, що дроби звели до спільного знаменника. Іноді наперед відомо, до якого саме спільного знаменника треба звести дроби. Тоді кожен дріб окремо зводять до заданого знаменника за відомим правилом.

Частіше новий знаменник наперед не задано. Тоді треба спочатку з’ясувати, до якого спільного знаменника можна звести дані дроби.

Як правило, дроби зводять до такого спільного знаменника, який е найменшим з усіх можливих. Такий знаменник називають найменшим спільним знаменником даних дробів.

Запам’ятайте!

Найменшим спільним знаменником дробів є число, що дорівнює найменшому спільному кратному (НСК) знаменників даних дробів.

Сформулюємо правило зведення дробів до найменшого спільного знаменника.

Запам’ятайте!

Правило зведення двох дробів до найменшого спільного знаменника

Щоб звести два дроби до найменшого спільного знаменника, треба:

1) знайти НСК знаменників даних дробів;

2) знайти додатковий множник для першого дробу;

3) звести перший дріб до нового знаменника;

4) знайти додатковий множник для другого дробу;

5) звести другий дріб до нового знаменника.

Задача 1

Зведіть до найменшого спільного знаменника дроби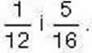

Розв’язання.

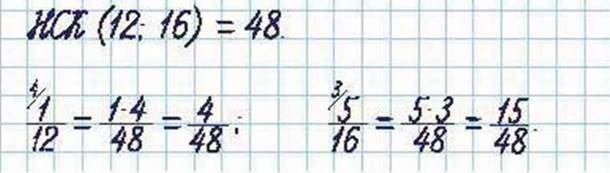
Наприклад:

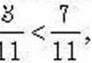оскільки В < 7; 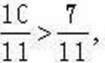оскільки 10 > 7.

? Чи можна порівняти два дроби з різними знаменниками? Так. Розглянемо приклад.

Задача 2. Порівняйте дроби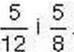

Розв’язання. Зведемо дані дроби до найменшого спільного знаменника 24. Тоді 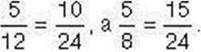Оскільки знаменники отриманих дробів є рівними, можемо порівняти їх чисельники:

10 < 15. Звідси: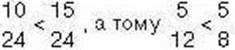

Дізнайтеся більше

Якщо два дроби мають однакові чисельники і різні знаменники, то їх можна порівняти, не зводячи до спільного знаменника. Для цього користуються правилом: із двох дробів з однаковими чисельниками більшим є той, у якого знаменник менший. Напри

Клад, 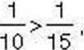оскільки 10 < 15. Спробуйте самостійно пояснити цей висновок за малюнками 4 і 5.

Мал. 4

Мал. 5

ПРИГАДАЙТЕ ГОЛОВНЕ

1. Що означає звести дріб до нового знаменника?

2. Яке число називають додатковим множником?

3. Поясніть, як знайти додатковий множник.

4. Сформулюйте правило зведення дробу до нового знаменника.

5. Яке число називають найменшим спільним знаменником дробів?

6. Сформулюйте правило зведення двох дробів до спільного знаменника.

7. Як порівняти два дроби з різними знаменниками?

РОЗВ’ЯЖІТЬ ЗАДАЧІ

240′. Чи можна звести дріб 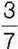до знаменника: 1) 15; 2) 21; 3) 27; 4) 42?

241′. Чи правильно, що:

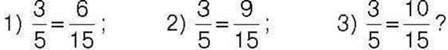
242′. Чи правильно, що найменшим спільним знаменником дробів 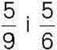є число: 1)9; 2) 6; 3) 54; 4) 18?

243°. Дано рівності: 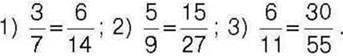Який додатковий множник використали, щоб отримати з першого дробу другий дріб?

244°. На який додатковий множник треба помножити дріб 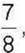щоб звести його до знаменника: 1) 24; 2) 48; 3) 96; 4) 120?

245°. Зведіть дріб 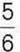до знаменника: 1) 12; 2) 18; 3) 24; 4) 48.

246°. Зведіть дроби 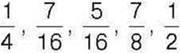до знаменника 32.

247°. Зведіть дроби 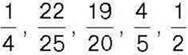до знаменника 100.

248°. До якого найменшого спільного знаменника можна звести дані дроби? Виконайте цю дію.

249°. До якого найменшого спільного знаменника можна звести дані дроби? Виконайте цю дію.

250°. Порівняйте дроби:

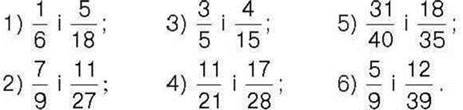
251 . Порівняйте дроби: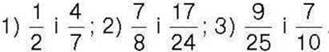

252°. Розмістіть у порядку зростання числа: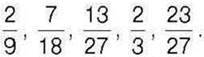

253°. Розмістіть у порядку спадання числа: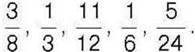

254. Зведіть до найменшого спільного знаменника дроби:

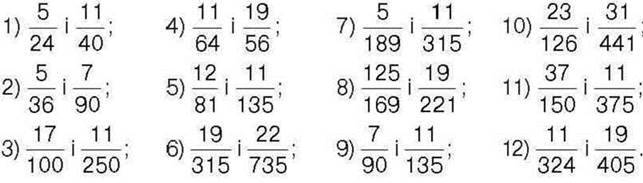
255. Зведіть до найменшого спільного знаменника дроби:

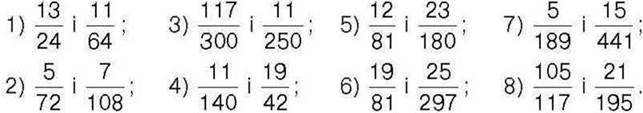
256. Які дроби зі знаменником 12 лежать між числами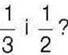

257. Які дроби зі знаменником 18 лежать між числами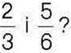

258. Накресліть координатний промінь (одиничний відрізок – 10 клітинок зошита). Позначте на цьому промені точки 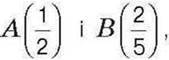а також усі точки з координатами виду 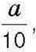де а – натуральне число. Яким числам відповідає одна й та сама точка? Запишіть відповідні рівності.

259. Накресліть координатний промінь (одиничний відрізок – 8 клітинок зошита). Позначте на цьому промені точки 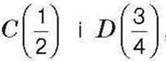а також усі точки з координатами виду 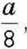де а – натуральне число. Яким числам відповідає одна й та сама точка? Запишіть відповідні рівності.

260. Зведіть до найменшого спільного знаменника дроби:

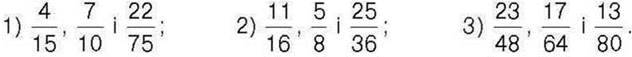
261. Зведіть до найменшого спільного знаменника дроби:

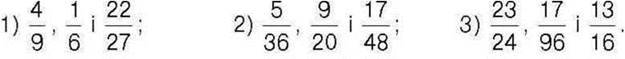
262. Порівняйте числа:

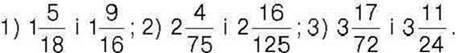
263. Порівняйте числа:

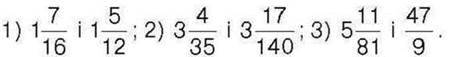
264. Через першу трубу басейн заповнюється за 10 год, а через другу – за 6 год. З якої труби витече більше води: з першої за 4 год чи з другої за 3 год?

265. Тканину червоного кольору за вдовжки 15 м розрізали на 6 рівних частин, а тканину зеленого кольору завдовжки 24 м – на 9 рівних частин. Частина тканини якого кольору довша?

266. У продуктовому магазині 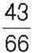усього товару – це хлібобулочні вироби, 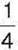– цукерки та печиво, 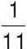– вода та соки. Яких продуктів у магазині найбільше?

267*. Порівняйте дроби, не зводячи їх до спільного знаменника:

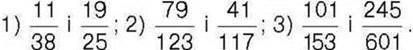
Відповідь поясніть.

268*. Порівняйте дроби, не зводячи їх до спільного знаменника:

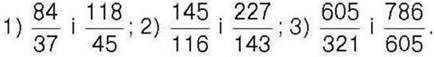
Відповідь поясніть.

269*. 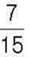одного числа дорівнюють 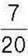другого числа. Яке з чисел більше?

270″. Який дріб більший: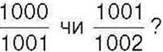

271*. Доведіть, що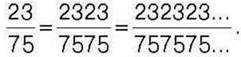

ЗАСТОСУЙТЕ НА ПРАКТИЦІ

272. Тато проходить за 10 кроків 9 м, а мама за 14 кроків – 10 м. Чий крок довший?

273. Улітку на дачі Настя зібрала 2 відра огірків за 40 хв, а її бабуся – 4 відра огірків за ЗО хв. Хто з них швидше збирав одне відро огірків?

274. Мама зліпила за 10 хв 60 пельменів, а донька за 15 хв – 90 пельменів. Хто з них ліпив більше пельменів за 1 хв?

ЗАДАЧІ НА ПОВТОРЕННЯ

275. У числі 347* замість зірочки вставте таку цифру, щоб отримане число ділилося: 1)на 9; 2)на З; 3) на 5.

276. Знайдіть площу найбільшої грані прямокутного паралелепіпеда, якщо його об’єм становить 360 см3, а два ребра дорівнюють 12 см і 40 мм.

(1 votes, average: 5.00 out of 5)

Ви зараз читаєте: ЗВЕДЕННЯ ДРОБІВ ДО СПІЛЬНОГО ЗНАМЕННИКА. ПОРІВНЯННЯ ДРОБІВ

« Обслуговування зовнішнього боргу

Стилістика власне неповних речень, еліптичних і приєднувальних неповних речень »

Related posts: