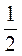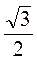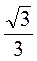Формули доповнення. Значення тригонометричних функцій кутів 30°, 45°, 60°
Урок № 57
Тема. Формули доповнення. Значення тригонометричних функцій кутів 30°, 45°, 60°
Мета: сформувати в учнів свідоме розуміння змісту та доведення теореми, що містить формули доповнення, а також наслідку з неї; домогтися засвоєння учнями способу обчислення та значень тригонометричних функцій кутів 30°, 45° і 60°. Закріпити знання вивчених формул та сформувати вміння їх застосовувати під час розв’язування задач.
Тип уроку: засвоєння вмінь та навичок.
Наочність та обладнання: конспект “Формули доповнення. Значення тригонометричних
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
З огляду на досить великий об’єм матеріалу, який слід вивчити на уроці, перевірку здійснюємо усно, за записами, виконаними на дошці заздалегідь.
III. Формулювання мети і завдань уроку
Поштовхом до інтелектуальної діяльності учнів може бути завдання, одного разу вже запропоноване та вдосконалене вчителем.
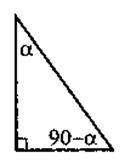
Завдання. Виконайте зображення прямокутного трикутника з катетами а, b і гіпотенузою с. Кути, протилежні катетам а, b, позначте відповідно?, ?. Запишіть, чому дорівнюють sin? та cos?. Порівняйте
Мета запропонованого завдання – наочно продемонструвати учням існування певних залежностей між тригонометричними функціями гострих кутів прямокутного трикутника. Далі слід наголосити на тому, що для гострих кутів будь-якого прямокутного, трикутника існує загальна властивість. Тому, узагальнивши проведені Спостереження для кутів, що мають із гострими кутами прямокутного Трикутника спільну властивість, ми дістанемо нові твердження. Вивчення цих тверджень та способу їх застосування – основна мета уроку.
IV. Актуалізація опорних знань та вмінь
Учням слід відтворити набуті ними раніше знання про властивість гострого кута прямокутного трикутника, медіани рівностороннього трикутника, а також теореми Піфагора, та поновити вміння використовувати ці знання під час розв’язування задач. Для цього учнями пропонується виконати усні вправи.
Виконання усних вправ
1. Знайдіть кут х на рис. 1.
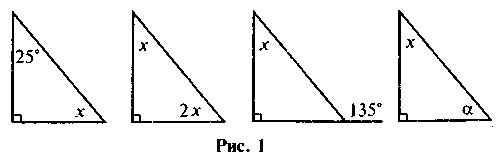
2. За даними рисунка 2 знайдіть  DAC, AD, якщо АВ = ВС,
DAC, AD, якщо АВ = ВС,  B = 60°.
B = 60°.
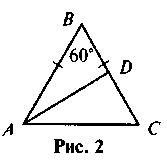
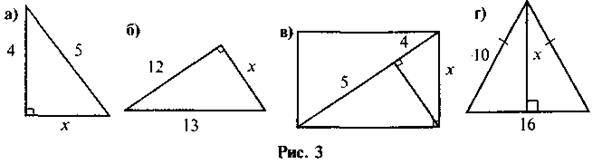
3. Знайдіть х на рис. 3.
V. Засвоєння знань
План вивчення нового матеріалу
1. Теорема (формули доповнення).
2. Наслідок з теореми.
3. Значення тригонометричних функцій кутів 30°, 45°, 60°.
@ Зміст матеріалу, поданого в п. 20.1 і 20.2 нового підручника, відрізняється від змісту відповідного пункту традиційного підручника лише тим, що з теореми (формули доповнення) виведено наслідок для тангенсу і котангенсу гострого кута. Доведення теореми та знаходження значень тригонометричних функцій кутів 30°, 45°, 60° здійснюється традиційним способом (через застосування теореми Піфагора, означення тригонометричних функцій та формул доповнення до прямокутних трикутників із гострими кутами 30° і 45°). Оскільки зміст матеріалу уроку грунтується на добре засвоєних знаннях учнів і вимагає спостережливості та вмінь виконувати обчислення відповідно до змісту теореми Піфагора, то вивчення матеріалу уроку проводиться у формі практичної роботи (можна в малих групах), результати якого після закінчення оголошуються, коригуються та узагальнюються, а також фіксуються в зошитах учнів у вигляді записів, аналогічних до записів конспекту 22.
Конспект 22 | |||
Формули доповнення. Значення тригонометричних функцій кутів 30°, 45°, 60° Формули доповнення: Якщо 0° < ? < 90°, то Sin (90° – ?) = cos?. Cos (90° – ?) = sin?. Tg (90° – ?) = ctg?. Ctg (90° – ?) = tg?. |
| ||
Значення тригонометричних функцій кутів 30°, 45°, 60° | |||
Функція | Кут? | ||
30° | 45° | 60° | |
Sin? |
|
|
|
Cos? |
|
|
|
Tg? |
| 1 |
|
Ctg? |
| 1 |
|
Після виконання цієї частини роботи вчитель має зробити акцент на тому, що, з огляду на широку вживаність записаних у таблиці чисел, їх треба вивчити напам’ять. Кращому запам’ятовуванню сприятиме застосування формул доповнення та існування певного закону у послідовності запису чисел (значення синусів кутів 30°, 45°, 60° є дробами, в знаменнику яких стоїть число 2, а в чисельнику – значення квадратного кореня з перших трьох натуральних чисел: 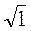 = 1,
= 1, 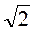 ,
, 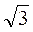 ), а також використовування інших мнемонічних прийомів (наприклад, виділення однакових чисел у таблиці однаковим кольором).
), а також використовування інших мнемонічних прийомів (наприклад, виділення однакових чисел у таблиці однаковим кольором).
VI. Формування первинних умінь
Виконання усних вправ
1. У прямокутному трикутника ABC з гіпотенузою АВ sin В = а. Чому дорівнює косинус кута А?
2. Чи можуть синус і косинус гострого кута прямокутного трикутника дорівнювати один одному? В якому випадку?
3. У прямокутному трикутнику ABC з гіпотенузою АВ tg А > tg B. Чи може один із цих тангенсів дорівнювати одиниці?
4. Кути? і? – гострі кути прямокутного трикутника. Знайдіть добуток tg? – tg?.
Виконання письмових вправ
1. Знайдіть гострий кут х, якщо:
А) sin x = cos 36°;
Б) cos x = sin 82°;
В) tg x = 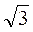 ;
;
Г) cos x = sin x.
2. Обчисліть:
а) sin 30° + tg 45°;
Б) cos 30° – tg 60°;
В) 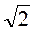 Sin 45° – cos 60°.
Sin 45° – cos 60°.
3. Кути А і В – гострі кути прямокутного трикутника. Знайдіть:
А) sin В і cos В, якщо cos A = 0,6;
Б) cos А і tg А, якщо sin В = 0,5.
4. Знайдіть гострий кут х, якщо:
A) tg х = ctg 22°;
Б) cos (90° – x) = 0,5.
@ Розв’язування запропонованих вправ сприяє закріпленню знань формул доповнення та значень тригонометричних функцій кутів 30°, 45°, 60°, а також формуванню вмінь використовувати ці знання під час розв’язування стандартних завдань на розуміння.
VII. Підсумки уроку
Знайдіть помилки в таких рівностях:
1) sin 12° = cos 78°;
2) sin 70° = sin 10°;
3) cos 53° = sin 47°;
4) cos 25° = sin 65°;
5) cos 21° = sin 69°;
6) sin 34° = cos 56°.
VІІІ. Домашнє завдання
Вивчити зміст і доведення теореми та наслідку з неї, значення тригонометричних функцій кутів 30°, 45°, 60°.
Розв’язати задачі.
1. Накресліть прямокутний трикутник.
А) Виміряйте катет і гіпотенузу трикутника й обчисліть їх відношення.
Б) Виділіть червоним кольором кут, синус якого знайдено, і синім кольором – косинус якого знайдено.
2. Знайдіть гострий кут х, якщо:
A) cos x = sin 50°;
Б) sin x = 0,5;
В) tg х = 1.
3. Обчисліть:
А) 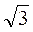 Cos 30° – cos 60°;
Cos 30° – cos 60°;
Б) cos 45° – sin45°;
В) sin 60° – tg 30°.
4. Знайдіть:
a) cos? і sin?, якщо sin (90° – ?) = 0,8;
Б) tg(90° – ?), якщо sina = 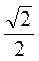 .
.
Повторити теорему Піфагора; тригонометричні тотожності; нерівність трикутника.