ДІЇ ЗІ СТЕПЕНЯМИ
РОЗДІЛ II ОДНОЧЛЕНИ
&6. ДІЇ ЗІ СТЕПЕНЯМИ
Ви знаєте, що додавання і віднімання – це дії першого ступеня, множення і ділення – дії другого ступеня, а піднесення до степеня – дія третього ступеня. Зі степенями можна виконувати всі ці дії. Наприклад:
33 + 32 = 27 + 9 = 36,
33 – 32 = 27 – 9 = 18,
33 ∙ 32 = 27 ∙ 9 = 243,
33 : 32 = 27 : 9 = 3,
(33)2 = 272 = 729.
Проте безпосередні обчислення не завжди легко виконувати, наприклад, якщо основа і показник кожного зі степенів – великі числа. Якщо ж степені задано в буквеному вигляді, тоді безпосередні
Тут дії зі степенями виконують на основі властивостей степенів. При цьому розрізняють два випадки: 1) рівні основи;
2) різні основи.
1. Дії першого ступеня зі степенями
Для степенів як з рівними, так і з різними основами виконуються переставний і сполучний закони додавання.
2. Дії другого ступеня зі степенями
Для степенів як з рівними, так і з різними основами виконуються переставний і сполучний закони множення, а також розподільний закон множення відносно додавання.
Інші властивості дій другого ступеня зі степенями дозволяють згортати в один степінь добуток
Запам’ятайте!
Теорема 1 (основна властивість степенів).
Добуток двох степенів з рівними основами дорівнює степеню з тією ж основою і показником, що дорівнює сумі показників множників:
An ∙ am = an+m
Дано: аn, аm, де а – будь-яке число, n і m – натуральні числа.
Д о в е с т и: an ∙ am = аn+m.
Доведення. Спираючись на означення степеня, спочатку розгорнемо кожний степінь у добуток, а потім згорнемо отриманий результат у степінь:
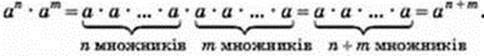
Отже, аn ∙ am = аn+m.
? Чи можна застосувати основну властивість степенів до множення кількох степенів з однією основою? Так.
Наприклад:
Аn ∙ аn ∙ аk = (аn ∙ аm) ∙ аk = аn+m ∙ аk = аn+m+k.
Запам’ятайте!
Теорема 2 (властивість частки степенів із рівними основами).
Частка двох степенів з рівними основами, відмінними від нуля, дорівнює степеню з тією ж основою і показником, що дорівнює різниці показників діленого і дільника:
Аn : аm = аn-m (n>m).
Д а н о: аn, аm, де а ≠ 0, n і m – натуральні числа, n > m.
Д о в е с т и: аn : am = аn-m.
Доведення. Спираючись на означення степеня, спочатку розгорнемо кожний степінь у добуток:
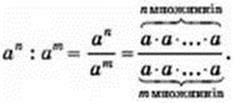
Оскільки n > m і для a ≠ 0  = 1,то в отриманому виразі можна виділити m множників
= 1,то в отриманому виразі можна виділити m множників  , що дорівнюють 1, і n – m множників, що дорівнюють а:
, що дорівнюють 1, і n – m множників, що дорівнюють а:

За означенням степеня:
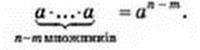
Отже, аn : аm = аn-m.
? Чому в теоремі 2 на показники степенів накладено обмеження n > m? Тому що для n ≤ m у частці дістанемо степінь, показник якого не є натуральним числом.
Зверніть увагу:
Дії другого ступеня зі степенями, що мають рівні основи, зводяться до відповідних дій першого ступеня з їх показниками:
– множення степенів – до додавання їх показників;
– ділення степенів – до віднімання їх показників.
Запам’ятайте!
Теорема 3 (властивість добутку степенів із різними основами і рівними показниками).
Добуток n-их степенів чисел а і b дорівнює n-му степеню добутку аb:
Аn ∙ bn = (аb)n.
Д а н о: an, bn, а і b – будь-які числа, n – натуральне число.
Д о в е с т и: аn ∙ bn = (ab)n.
Д о в е д е н н я. Спираючись на означення степеня, спочатку розгорнемо колений степінь у добуток, перегрупуємо множники, а потім згорнемо отриманий результат у степінь:
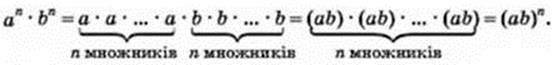
Отже, аn ∙ bn = (ab)n.
Сформулюємо без доведення властивість степеня добутку двох чисел: n-й степінь добутку чисел а і b дорівнює добутку їх n-их степенів. Тобто для будь-яких чисел а i b:
(ab)n = an ∙ bn.
Розглянемо властивість ділення степенів.
Теорема 4 (властивість частки степенів із різними основами і рівними показниками).
Частка n-их степенів чисел а і b (b ≠ 0) дорівнює n-му степеню частки  :
:
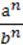 = (
= ( )n
)n
Д а н о: аn, bn, а – будь-яке число, b ≠ 0, n – натуральне число.
Д о в е с т и:
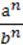 = (
= ( )n.
)n.
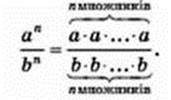
Д о в е д е н н я. Спираючись на означення степеня, розгорнемо в добуток степені, що є відповідно діленим і дільником:
Перегрупуємо компоненти отриманого виразу і застосуємо означення степеня:
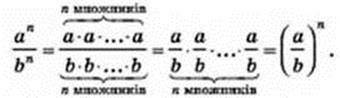
Отже,
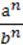 = (
= ( )n.
)n.
Сформулюємо без доведення властивість степеня чистки двох чисел: n-й степінь частки чисел а і b (b ≠ 0) дорівнює частці їх n-их степенів. Тобто для будь-якого числа а і b ≠ 0:
( )n =
)n = 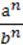
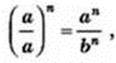
Або (а : b)n = аn : bn.
3. Дії третього ступеня зі степенями
Ви знаєте, що до дій третього ступеня належить дія піднесення до степеня. Степені також можна підносити до степеня з натуральним показником. Розглянемо властивість такої дії.
Запам’ятайте!
Теорема 5 (властивість піднесення степеня до степеня).
Для степеня з показником m його n-й степінь дорівнює степеню з тією ж основою і показником mn:
(аm)n = аmn
Д а н о: аm, (аm)n, де m і n – натуральні числа.
Д о в е с т и: (аm)n = аmn.
Доведення. Скористаємось означенням та основною властивістю степеня. Тоді дістанемо:
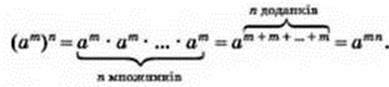
Отже, (аm)n = аmn.
У виразі (аm)n показники m і n називатимемо відповідно внутрішнім і зовнішнім показниками.
Зверніть увагу:
Дія третього ступеня зі степенем зводиться до відповідної дії другого ступеня із внутрішнім і зовнішнім показниками:
Піднесення степеня до степеня – до множення двох показників.
Дізнайтеся більше
Михайло Пилипович Кравчук (1892-1942) – український математик, академік АН УРСР (з 1929), доктор фізико-математичних наук (з 1924), професор Київського Політехнічного інституту. Народився в селі Човницях на Волині в сім’ї землеміра.
М. П. Кравчук був учителем багатьох видатних людей минулого століття: Архипа Люльки – конструктора реактивних авіадвигунів, Сергія Корольова – конструктора космічних кораблів, академіка Володимира Челомея. Методи М. П. Кравчука були використані в США, Японії та інших країнах для моделювання кібернетичної техніки, а також для створення першого у світі комп’ютера М. П. Кравчук був співавтором першого тритомного словника української математичної термінології.

ПРИГАДАЙТЕ ГОЛОВНЕ
1. Які дії зі степенями можна виконувати?
2. Які закони справджуються для дій зі степенями першого ступеня; другого ступеня?
3. Яка основна властивість степенів? Доведіть її.
4. Сформулюйте і доведіть властивість частки степенів з рівними основами.
5. Яка властивість добутку степенів з різними основами і рівними показниками? Доведіть її.
6. Сформулюйте і доведіть властивість частки степенів з різними основами і рівними показниками.
7. Яка властивість піднесення степеня до степеня? Доведіть її.
РОЗВ’ЯЖІТЬ ЗАДАЧІ
242. Яка з формул є правильною:
1) bn ∙ bm = 2bn∙m;
2) bn ∙ bm = bn ∙ m;
3)bn ∙ bm = bn+m?
243. Назвіть показник степеня, якому дорівнює добуток степенів:
1)53 ∙ 52;
2) 66 ∙ 610;
3)7 ∙ 74;
4)82 ∙ 82.
244. Яка з формул є правильною:
1) сn : сm = сn∙m ;
2) сn : сm = сn:m;
3) сn : сm = сn-m?
245. Назвіть показник степеня, якому дорівнює частка степенів:
1) 53 : 52;
2) 610 : 66;
3) 74 : 7;
4) 82 : 82.
246. Назвіть основу степеня, якому дорівнює добуток степенів:
1) 43 ∙ 23;
2) 36 ∙ 126;
3)1610 ∙ 210;
4)82 ∙ 82
247. Чи є правильною рівність:
1)(12 + 4)3 = 123 + 43; 3) (12 ∙ 4)3 = 123 + 43;
2)(12 + 4)3 = 123 – 43; 4) (12 ∙ 4)3 = 123 ∙ 43?
248. Назвіть основу степеня, якому дорівнює частка степенів:
1)43 : 23; 2) 126 : 36; 3) 1610 : 210; 4) 82 : 82.
249.Чиє правильною рівність:
1) (12 – 4)3 = 123 – 43; 3) (12 : 4)3 = 123 – 43;
2) (12 – 4)3 = 123 : 43; 4) (12 : 4)3 = 123 : 43?
250. Яка з формул є правильною:
1) (dn)m = dn+m;
2) (dn)m= dn-m;
3) (dn)m= dn:m ;
4) (dn)m = dn∙m?
251. Назвіть показник степеня, якому дорівнює степінь степеня:
1) (53)2; 2) (66)10; 3)(71)4; 4)(82)2.
252. Запишіть у вигляді степеня з основою 2:
1) 28 ∙ 23;
2) 25 ∙ 26 ∙ 210;
3) 2 ∙ 213 ∙ 216;
4) 22 ∙ 24 ∙ 26 ∙ 28 ∙ 210.
253. Запишіть у вигляді степеня з основою 8:
1) 85∙ 8;
2) 816 ∙ 89 ∙ 820;
3) 83 ∙ 83 ∙ 84.
254. Запишіть у вигляді степеня добуток:
1) 107 ∙ 105;
2) 0,3 ∙ 0,32;
3) (-4,5)33 ∙ (-4,5)44 ∙ (-4,5)55;
4) -4 ∙ (- 4)9;
5) а ∙ a54 ∙ а36 ∙ а ∙ а8;
6) (-n)4 ∙ (-n)4 ∙ (-n)4;
7)2,14 ∙ 2,13 ∙ 2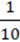 ;
;
8) (-xy)5 ∙ (-xy)8 ∙ (-хy)32;
9)  ∙ (
∙ ( )2 ∙ (
)2 ∙ ( )3b≠0;
)3b≠0;
10. (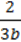 )2 ∙ (
)2 ∙ (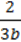 )102 ∙ (
)102 ∙ (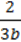 )202 (b≠0).
)202 (b≠0).
255. Запишіть у вигляді степеня добуток:
1) 54 ∙ 53 ∙ 56 ;
2) 0,01 ∙ 0,019;
3) с2 ∙ с8;
4) (-p)3 ∙ (-p)27.
5) m4 ∙ m7 ∙ m12;
6) а ∙ а67 ∙ а3 ∙ а ∙ а;
7) (-x)2∙ (-x)15∙ (-х)23;
8)  ∙ (
∙ ( )6 ∙ (
)6 ∙ ( )4c≠0;
)4c≠0;
256. Запишіть у вигляді добутку степенів:
1)5m+n;
2) 10n+p;
3) 0,8n+m+1.
257. Подайте степінь а64 у вигляді добутку двох степенів, один з яких:
1) а32; 2) а62; 3) а14; 4) а30.
258. Подайте степінь mn25 у вигляді добутку двох степенів, один з яких:
1) m2; 2) m5; 3) m15; 4) m24.
259. Запишіть у вигляді степеня з основою 11:
1)1114 : 114;
2) 1110 : 116 : 111;
3) 1126 : 1113 : 1111.
260. Запишіть у вигляді степеня з основою 8:
1) 85 : 8;
2) 816 : 89 : 82;
3) 8а : 83 : 84.
261. Обчисліть:
1) 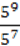 ;
;
2) (0,2)14: ( )10;
)10;
3) 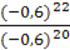 .
.
262. Запишіть у вигляді степеня частку:
1) 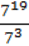 ;
;
2) 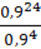 ;
;
3) 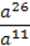 (a≠0);
(a≠0);
4) 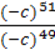 (c≠0).
(c≠0).
263. Запишіть у вигляді частки степенів:
1) 2n-m;
2) 9n-3;
3)10010-n.
264. Запишіть у вигляді степеня з основою 0,1:
1)0,19 ∙ 0,116: 0,16;
2)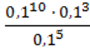 ;
;
3)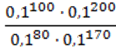 .
.
265. Запишіть у вигляді степеня з основою 5:
1) 56 ∙ 59 : 53;
2)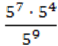 ;
;
3) 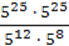 .
.
266. Запишіть у вигляді степеня з основою 12:
1) 25 ∙ 65;
2) 37 ∙ 47;
3) 24 ∙ 24 ∙ 34.
267. Запишіть у вигляді степеня з основою 30:
1) 321 ∙ 1021;
2) 69 ∙ 59;
3)26 ∙ 36 ∙ 56.
268. Знайдіть *, якщо:
1) 245 = 25 ∙ (*)5;
2) 367 = 67 ∙ (*)7;
3) 362 = 22 ∙ (*)2 ∙ 92.
269. Знайдіть *, якщо:
1)10011 = 211 ∙ (*)11;
2) 1008 = 258 ∙ (*) 8;
3) 10034 = 234 ∙ (*)34 ∙ 534.
270. Запишіть у вигляді степеня з основою 2:
1) 128 : 68;
2) 67 : 37;
3) 164 : 84;
4) 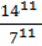 .
.
271. Запишіть у вигляді степеня з основою 3:
1) 1510 : 510; 2)273 : 93; 3)425 : 145.
272. Обчисліть:
1) (-6 ∙ 0,3) 3 : (-6)3;
2) (4 ∙ 3)3 : 122;
3) 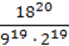 .
.
4) 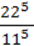 .
.
273. Обчисліть:
1) (5 ∙ 8)4 : (8)4;
2) (2 ∙ 0,25)5 : 0,255;
3) 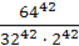 .
.
274. Запишіть у вигляді степеня:
1) (а3)2; 2) (а5)10; 3) (m4)6; 4) (сm)2.
275. Запишіть у вигляді степеня:
1)(35)10;
2)((-4)11)9;
3) ((-3,5)10)4;
4) ((-1)4)13;
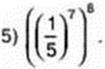
276. Обчисліть:
1) ((-2)2)3;
2) ((-10)2)3;
3) ((-1 )6)3.
277. Знайдіть а6, якщо а3 дорівнює:
1) 10; 2) -2; 3) -0,3; 4)  .
.
278. Знайдіть n:
1) (235)36 = (235n)9; 3) (4,5)36 = (4,52)n;
2) (8)36 = (8n)6; 4) (5,09)36 = (5,09n)2.
279. Поставте знак <, >, = між виразами:
1) ((- 2)6)3 і ((- 2)5)2; 3) (- 1,7)5 і (02)2;
2) ((- 2)5)2 і ((- 2)2)5; 4) ((-1 )5)2і (-1)32.
280. Запишіть у вигляді степеня з основою 3:
1) (33)5 ∙ 32 : 312;
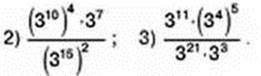
281. Запишіть у вигляді степеня з основою 8:
1)(810)8 : (87)10;
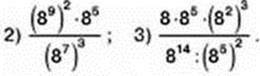
282. Запишіть у вигляді степеня з основою 0,5:
1)0,25 – 0,125;
2)0,5 ∙  ∙
∙  ;
;
3)0,00625 ∙ 2 ∙ 5.
283. Запишіть у вигляді степеня з основою -2:
1) -8 ∙ 4;
2) -2 ∙ 4 ∙ 16;
3) -32 ∙ 64.
284. Запишіть у вигляді степеня:
1) (-20)4 ∙ 203; 3) а1 ∙ а2 ∙ а3 ∙…∙ а8;
4) а2 ∙ а4∙…∙а10.
285. Подайте степінь а30 у вигляді частки двох степенів, якщо дільник дорівнює:
1)а8; 2) а5; 3)а16; 4 )а29.
286. Знайдіть х, якщо b ≠ 0, a ≠ 0 і:
1) а12b36 = а2b10 ∙ х; 3) а12b36 = a22b36 : х;
2) а12b36 = а4b6 – х; 4) a12b36 = a100b100 : х.
287. Знайдіть х, якщо b * 0, a * 0 і:
1) а12b36 = аb ∙ х; 3) a12b36 = х : ab;
2 )а12b36 = b30 ∙ х; 4) a12b36 = х : b30.
288. Знайдіть значення виразу а2 ∙ b2, якщо:
1) а = 27, b = –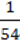 ; 2) а = -36, b = -1
; 2) а = -36, b = -1 .
.
289. Знайдіть добуток:
1)2,5 ∙ 103см і 2 ∙ 102м; 3) 5,4 ∙ 103кг і 1,5 ∙ 1010;
2) 8 ∙ 109м і 0,1 ∙ 103 км; 4) 122 ∙ 108 г і 0,5 ∙ 104.
290. Знайдіть частку:
1) 6 ∙ 103м і 3 ∙ 102 см; 3) 104 кг і 5 ∙ 107 г;
2) 106см і 0,1 ∙ 103 м; 4) 4,8 ∙ 106 г і 0,3 ∙ 104.
291. Знайдіть значення виразу (а ∙ b)3 : с3, якщо:
1) а = 7, b = -6,5, с =45,5;
2) а = , b = 6
, b = 6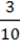 , с = 4,5.
, с = 4,5.
292. Запишіть вираз у вигляді степеня:
1) ( )2 ∙ 0,25 ∙ 412; 4) 514 ∙ 0,018 ∙ 52 ∙ 0,018;
)2 ∙ 0,25 ∙ 412; 4) 514 ∙ 0,018 ∙ 52 ∙ 0,018;
2) 8 ∙ 0,32 ∙ 85 ∙ 0,34; 5) (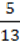 )65 ∙ (2
)65 ∙ (2 )35;
)35;
3) ( )4 ∙ (1
)4 ∙ (1 )11; 6) (
)11; 6) (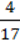 )642 ∙ 4,2535;
)642 ∙ 4,2535;
293. Винесіть за дужки 3n:
1) 38n + 3n+6; 2) 3n-2 ∙ 32n; 3)33n+5 + 3n+1.
294. Винесіть за дужки 2n:
1)25n + 2n+1; 2)2n – 2n ∙ 22n; 3)25n+2 – 3 ∙ 2n+3.
295. Подайте степінь 512 у вигляді степеня з основою:
1) 56; 2) 52; 3) 53; 4)54
296. Подайте степінь 442 у вигляді степеня з основою:
1)47; 2) (-4)6; 3)16; 4)64.
297. Знайдіть m12, якщо m2 дорівнює:
1)10; 2)0,1; 3)  .
.
298. Знайдіть с6, якщо с3 дорівнює:
1) -10; 2) 0,1; 3) – .
.
299. Запишіть у вигляді степеня:
1)((22)3)4; 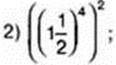
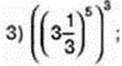
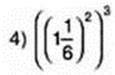
300. Спростіть вираз:
1) ((2а5)2 ∙ а3)6 ∙ 0,5а2 : (4а10)3 (а ≠ 0);
2) (6а4)2 ∙ с3 ∙ а6)2 : (27а4 ∙ (4с)3) (с ≠ 0, а ≠ 0);

301. Спростіть вираз:
1) (а16а4)3 : (а10а3)2(а ≠ 0); 3) (а16 : а4)3 ∙ (а10 : а3)2(а ≠ 0);
2) (а16 а4)3 – (а10а3)2; 4) (а16 : а4)3 : (а10 : а3)2(а ≠ 0).
302. Обчисліть:
1) -5 ∙ ((- 5)3)4 : 255 – (-10)2;
2) ((- 1)3)7 : 54 ∙ ((-50)2)2;
3) ( )4 ∙ (-
)4 ∙ (- 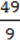 )2;
)2;
4) – 23 ∙ (- 5)2 ∙ (- 22) ∙ (- 5)3
303. Запишіть у вигляді степеня:
1) (а8)n : (аn)6(а ≠ 0);
2) (хm)n – (xn);
3) 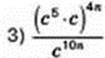 ∙ (c5n+2)2 (c ≠ 0);
∙ (c5n+2)2 (c ≠ 0);
4) (a2+n)n ∙ an(1-n) : (-a)2n (a ≠ 0).
304. Розв’яжіть рівняння:
1) 67(х8 ∙ (-х)8)3 = 0; 2) ((16 + 4х)2)5 = 0.
305. Розв’яжіть рівняння:
1) 53 ∙ (х3- (-х)3)6 = 0; 2) ((1,2 – 3х)4)6 = 0.
306. Порівняйте значення виразів:
1)((-4)3)5 і ((-4)5)7; 2) -98 і (-3)3; 3) 530 і 360; 4) 108 і 912.
307. Визначте знак виразу:
1) ((-а)3 ∙ (-а)5)7, якщо а < 0;
2) (-х)3 ∙ (-x ∙ у3)15, якщо х < 0, у > 0.
308. Якою цифрою закінчується число:
1) 545; 2) 1023; 3)610; 4) 111222?
309. Винесіть за дужки аn:
1) 2аn + а4n + 2; 2)а2nс + аn + 10 + аn.
310. Знайдіть знаменник дробу 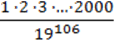 Після скорочення.
Після скорочення.
311. Розв’яжіть рівняння:
1) (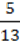 )4 ∙ 5,24 – х = 2; 3) 812 – х2 = 344 – 174 ∙ 24;
)4 ∙ 5,24 – х = 2; 3) 812 – х2 = 344 – 174 ∙ 24;
2) х : 73 = ( )3 ∙ (-0,25)3; 4)-12х = 67 – (
)3 ∙ (-0,25)3; 4)-12х = 67 – ( )5 ∙ 0,755.
)5 ∙ 0,755.
312. Розв’яжіть рівняння:
1) 5х = (-1,6)4 : (0,84 : 0,54); 3) 48 = (367 : 97) ∙ х2;
2) 0,56 : ( )5 = 32х; 4) 0,125 ∙
)5 = 32х; 4) 0,125 ∙ 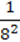 Х = (2
Х = (2 )3: 173.
)3: 173.
313. Знайдіть значення виразу
((а1)100) – 1) ∙ ((а2)50) – 1) ∙ ((а4)26) – 1) ∙ ((а5)20) – 1) ∙ ((а10)10) – 1) ∙ ((а20)50) – 1) ∙ ((а25)4) – 1) ∙ ((а50)2) -1) ∙ ((а100)1) – 1), якщо:
1)а = -1; 2)а = 1; 3)а = 0.
314. Доведіть, що число З2016 закінчується цифрою 7.
315. Якою цифрою закінчується число:
1) 209209; 2)20138; 3) 2722; 4) 445?
316. Порівняйте значення виразів:
1) 368 і 48 ∙ 37; 3) 1520 i 99 ∙ 521; 5)2812 і 918;
2) 616 ∙ 217 і 414 ∙ 316; 4) 49 ∙ 612 і 811 ∙ 38; 6) 1124 i 536.
317. Обчисліть
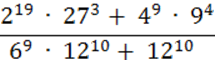
ЗАСТОСУЙТЕ НА ПРАКТИЦІ
318. Відстань від Землі до Сонця 150 ∙ 106 км. За який час світло подолає цю відстань, якщо швидкість світла у вакуумі дорівнює 3 ∙ 108 м/с?
319. Апогей – це найбільш можлива відстань від Землі до Місяця. Вона становить близько 4 ∙ 105 км. За який час космічний апарат, що рухається зі швидкістю 2 ∙ 108 м/год, подолає цю відстань?
ЗАДАЧІ НА ПОВТОРЕННЯ
320. Знайдіть значення виразу:
1) (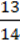 –
– 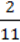 –
– 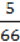 : 2
: 2 ) ∙ 1
) ∙ 1 : (3,2 + 0,8(5,5 – 3
: (3,2 + 0,8(5,5 – 3 );
);
2) 43,75 : 11 + 12
+ 12 ∙ 3
∙ 3 – 23,4 : 1,8.
– 23,4 : 1,8.
321. Знайдіть різницю виразу а – с і числа р, якщо:
1) а = 93,06, с = 21,65, р = 103,06;
2) а = 340,5, с = 20,05, p = 214,5.
322. прямокутнику зі сторонами 10 дм і 20 дм кожну сторону збільшили на 50 %. Якого периметра прямокутник одержали.
323. У трикутнику зі сторонами 10 см, 8 см і 6 см кожну сторону зменшили на 20 %. На скільки сантиметрів зменшився периметр трикутника?