Формули суми (різниці) однойменних тригонометричних функцій. Перетворення добутку тригонометричних функцій у суму
УРОК 15
Тема. Формули суми (різниці) однойменних тригонометричних функцій. Перетворення добутку тригонометричних функцій у суму
Мета уроку: вивчення формул суми і різниці однойменних тригонометричних функцій і формул перетворення добутку тригонометричних функцій у суму. Формування умінь учнів застосовувати вивчені формули для спрощення виразів та обчислень.
Обладнання. Таблиця “Формули перетворення суми в добуток (добутку в суму)”.
І. Перевірка домашнього завдання
1. Два учні на дошці розв’язують № 26 (1) і
2. Розв’язування аналогічних вправ. Спростіть вирази:
А)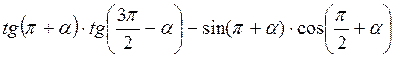 
;
Б)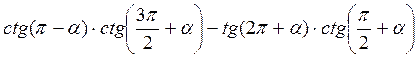 
;
В)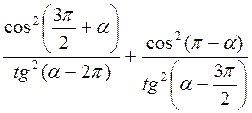 
;
Г)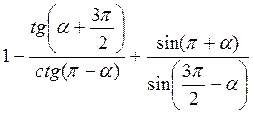 
.
Відповідь: а) соs2 ?; б)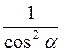 
; в) 1; г) tg?.
II. Повідомлення теми і завдань уроку
III. Сприймання і усвідомлення нового матеріалу
Демонструється таблиця 7.
|
;
.
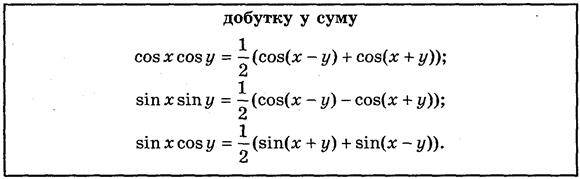
Пояснення вчителя
1.
Позначимо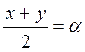 
, 
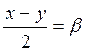, тоді? + ? = x, ? – ? = y, і тому
1) sin х + sin y = sin(? + ?) + sin(? – ?) = sin? – соs? + соs? – sіn? + sin? – cоs? – cos? – sіn? = 2sіn? – соs? = 2sіn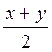 
Соs 
.
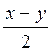Отже, сума синусів дорівнює подвоєному добутку синуса півсуми на косинус піврізниці.
Для суми косинусів маємо:
2) соs х + соs у = соs(? + ?) + соs(? – ?) = соs? соs? – sіn? sin? + соs? соs? + sіn? sіn? = 2 соs? соs? = 2 соs 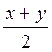Соs .
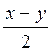Отже, сума косинусів дорівнює подвоєному добутку косинуса півсуми на косинус піврізниці.
Для різниці косинусів маємо:
3) соs х – соs у = соs(? + ?) – соs(? – ?) = соs? соs? – sіn? sin? – соs? соs? – sіn? sіn? = – 2 sin? sin? = 2 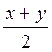sin Sin .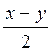
Отже, різниця косинусів дорівнює числу, протилежному подвоєному добутку синуса півсуми на синус піврізниці.
4) sin х – sin y = sin х + sin(-y) = 2 sin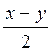Соs .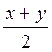
Отже, різниця синусів дорівнює подвоєному добутку синуса піврізниці на косинус півсуми.
2. Для одержання формул перетворення добутку у суму випишемо підряд чотири формули:
Sin(x + у) = sin x cos у + cos x sin у; (1)
Sin(x – у) = sin x cos у – cos x sin у; (2)
Cos(x + у) = cos x cos у – sin x sin у; (3)
Cos(x – у) = cos x cos у + sin x sin у. (4)
Віднявши почленно із рівності (4) рівність (3), одержимо:
Cos(x – у) – cos(x + у) = 2 sin x sin у або sin x sin у = 
(cos(х – у) – cos(x + y))
Добуток синусів двох чисел дорівнює піврізниці косинуса різниці і косинуса суми цих чисел.
Додавши почленно рівності (4) і (3), маємо:
Соs(x – у) + соs(х + у) = 2 соs х соs у або cos x cos у = (cos(x – у) + cos(х + у))
Добуток косинусів двох чисел дорівнює півсумі косинуса різниці і косинуса суми цих чисел.
Додавши почленно рівності (1) і (2), одержимо
Sin(x – у) + sin(х + у) = 2 sin x cos у або sin x cos у = (sin(x – у) + sin(x + у))
Добуток синуса одного числа на косинус другого числа дорівнює півсумі синуса різниці і синуса суми цих чисел.
Виконання вправ
1. Спростіть вирази:
А)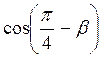 
– 
;
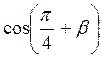Б)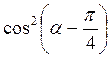 
– 
;
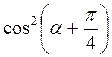В) sіn? –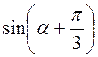 
;
Г)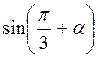 
+
.
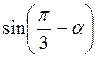Відповідь: а) 
Sin?; б) sin 2?; в)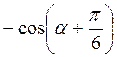 
; г) 
Соs?.
2. Обчисліть:
А) соs 22° – соs 38°;
Б) sin 5° + sin 55°.
Відповідь: а) sіn 8°; б) соs 25°.
3. Перетворіть в добуток:
А) соs 2? + соs 14? + соs 6? + соs 10?;
Б) sin 4? + sin 10? + sin 22? + sin 16?.
Відповідь: а) 4соs 2? соs 4? соs 8?; б) 4 соs 3? соs 6? sіn 13?.
4. Доведіть тотожність:
А)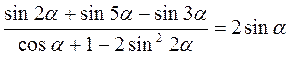 
; б)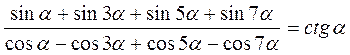 
.
IV. Підведення підсумків уроку
V. Домашнє завдання
Розділ І § 10 (5, 6). Запитання і завдання для повторення до розділу І № 69-70. Вправи № 52 (8; 15), № 53 (8; 15; 16)
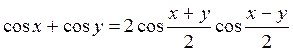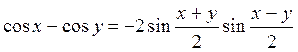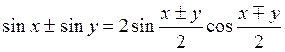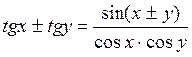(1 votes, average: 5.00 out of 5)
Loading...