Геометричні перетворення у просторі. Рухи
306.


Пряма і площина відображуються на себе відносно будь-якої точки, що належить їм.
307.
Два нерівні відрізки бути симетричними відносно деякої точки не можуть.
308.
Відносно початку координат:
Точці А(1; -3; 2) симетрична A1(-1; 3;-2);
Точці В(-5; 0; 2) – B1(5; 0; -2);
Точці С(3; -1; 0) – С1 (-3; 1; 0);
Точці D(0; 0; 0) – D1(0; 0; 0).
309.
Якщо т. А і т. В симетричні відносно т. М, то М – середина АВ;
М(-1; 3; 1). т. М, – симетрична т. М відносно т. A, M1(x; y; z).
А – середина 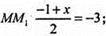
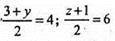
Х = -5; у = 5; z = 11. Отже M1(-5; 5; 11).
Т. М2 – симетрична т. М відносно т. B(1; 2; -4).
М2(x1; у1; z1),
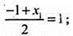
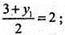
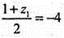
X1 = 3; у1 = 1; z1 = -9.
Отже, М1 (3; 1;-9).
310.
Якщо сфери симетричні, то радіуси сфер рівні R = 2.
О1 – центр шуканої сфери, симетричний центру O(4; 1; 2) відносно S(2; 3; -2).
О1 (х; у; z) 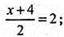
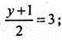
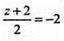
Х = 0; у = 5; z = -6.
Тоді шукана сфера задається рівнянням: x2 + (у – 5) 2 + (z + 6)2 = 4.
311.
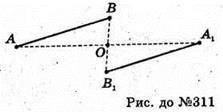
Т. А1 лежить на промені АО, який лежить
Отже, А1 ? (ОАВ). т. B1 лежить на промені ВО, який лежить в площині (ОАВ).
Отже, B1 ? (ОАВ). Оскільки дві точки лежать в площині (ОАВ),
То відрізок А1В1 лежить в площині (ОАВ).
312.
А)
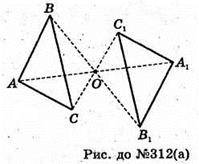
ΔA1B1С1 і ΔАBС симетричні відносно т. О;
Б)
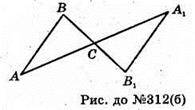
ΔA1СB1 симетричний ΔАСВ відносно т. С;
В)
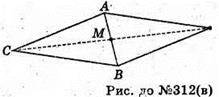
ΔABC1 симетричний ΔАВС відносно т. М – середини АВ.
313.
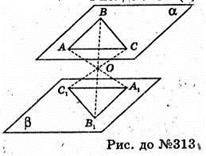
АА1В1С1 симетричний ΔАВС відносно т. О.
ВО = ОB1; ОС = ОС1; ∠BOC = ∠B1OC1. Звідси ΔBОС = ΔB1ОС1,
Звідси ∠ОВС = ∠ОВ1C1, але ці кути – внутрішні різносторонні
При прямих ВС, B1С1 і січній BB1. Звідси BC? B1C1, аналогічно BA? B1A1.
Тоді площина (ABС) ? (A1B1С1), тобто ΔАВС і ΔA1B1C1
Лежать в паралельних площинах.
314.
A)
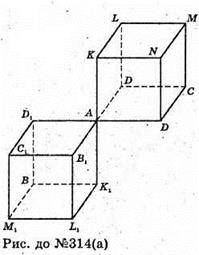
M1N1K1L1C1D1AB1 симетричний ABCDKLMN відносно т. А.
Б)
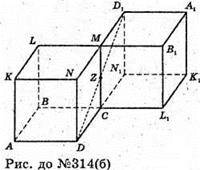
Куб CN1K1L1MD1A1B1 симетричний кубу ABCDKLMN
Відносно т. Z – середини ребра CM.
В)
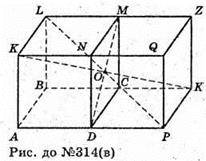
Куб DCKPNMZQ симетричний кубу ABCDKLMN
Відносно т. О – центра грані DNMC.
315.
Якщо т. А і С симетричні відносно т. В, а т. В і D симетричні відносно т. С,
То всі ці точки лежать на одній прямій, тому, через усі ці точки
Можна провести безліч площин і одну пряму.
316.
Ні, не можуть. Якщо відрізки симетричні, то вони лежать на паралельних прямих.
317.
Центрально-симетричною:
А) правильна трикутна призма не може бути;
Б) правильна чотирикутна призма є;
В) правильна п’ятикутна призма не може бути;
Г) правильна шестикутна призма є.
318.
Не має.
319.
Якщо многогранник має центр симетрії, то при центральній симетрії відносно цього центра симетрії многогранник перейде сам в себе. Тоді одна з вершин перейде в іншу вершину і т. д. Отже, центр симетрії знаходиться на однаковій відстані від вершин, тобто є центроїдом його вершин.
320.
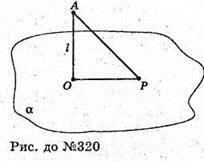
Пряма l + α. т. А? l, Р? α.
При центральній симетрії ΔАОР перейде в ΔA1Ο1P1),
Причому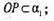 α ? α1; ΔAOP = ΔA1OP, тому
α ? α1; ΔAOP = ΔA1OP, тому
∠A1O1P1 = ∠AOP = 90°, тому A1O1 + α, або l1 + α.
Отже, пряма, перпендикулярна до площини, перейде в пряму,
Перпендикулярну до площини.
322.
Дана площина х – 2у + 3z – 2 = 0 перетинає вісь X у т. (2; 0; 0),
Вісь Y у т. (0; -1; 0), вісь Z у т. 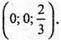
Тоді площина, симетрична даній площині, перетинатиме вісь
X у т. (-2; 0; 0), вісь У у т. (0; 1; 0), вісь Z у т. 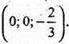
Тоді 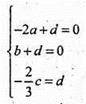
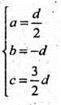
Ax+ by + cz + d = 0; 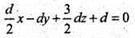
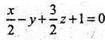 або x – 2y + 3z + 2 = 0 – рівняння шуканої площини.
або x – 2y + 3z + 2 = 0 – рівняння шуканої площини.
323.
Пряма А1В1 симетрична прямій АВ відносно початку координат.
Тоді A1(-1; 2; -4), B1(-2; 1; -3. Пряма A1B, задається рівнянням
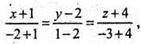 або
або 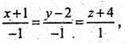 або
або 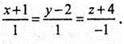
324.
А)
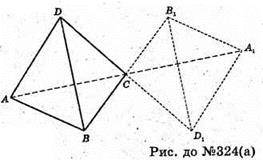
Тетраедр A1B1CD1 симетричний тетраедру ABCD відносно вершини С;
Б)
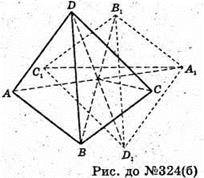
Тетраедр симетричний тетраедру A1B1C1D1 відносно т. О – центра грані BCD;
В)
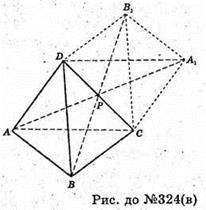
Тетраедр A1B1CD симетричний тетраедру ABCD відносно т. Р – середини ребра DC.