Геометричні тіла і многокутники
868.
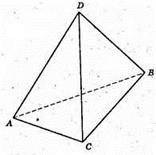
ABCD – тетраедр, 6 ребер, 4 вершини, 4 грані.
869.
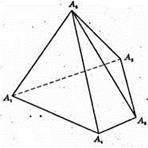
Многогранник A1A2A3A4A5, 5 граней, 5 вершин, 8 ребер.
870.
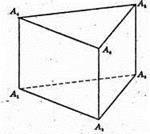
Многогранник, 5 граней, 6 вершин, 9 ребер.
872.
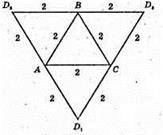
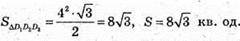
873.
Див. рис. з № 872
S пов. тетр.=36 см2, S грані = 36 : 4 = 9, SABCD = 9 см2, а = ?
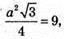
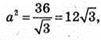
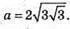
874.
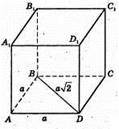
ABCDA1B1C1D 1 – куб, АА1 = а
А) відстань між його протилежними
Б) відстань між протилежними ребрами дорівнює 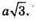
В) відстань між найближчими вершинами дорівнює а;
Г) відстань між найвіддаленішими вершинами (АС1) дорівнює 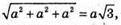
875.
Ребро куба а. Довжина його діагоналі АС (див. рис. № 874).
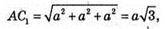
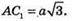
876. Площа поверхні паралелепіпеда дорівнює подвоєній сумі трьох
Різних його граней.
S пов. парал. = 2 × (2 + 3 + 4) = 18 (м2). S = 18 см2.
877.
S пов. куба = 6 × а2
А2 = 3а1; S1= 6а12, S2 =6 × 9а12, S2 = 9 × S1, S2: S1 = 9 : 1. 9 : 1.
878.
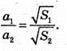
881.
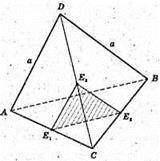
ABCD – правильний тетраедр, ребро а.
АЕ1 = СЕ1, СЕ2 = ВЕ2, СЕ3 = DE3.
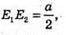
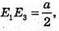
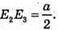
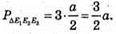
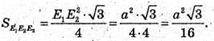
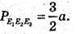
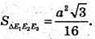
882.
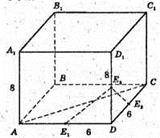
ABCDA1B1C1D1 – прямокутний паралелепіпед.
DA = 6 см
DC = 6 см
DD1 = 8 см
AE1 = DE1
DE2 = CE2
DE3 = E3D1
PΔE1E2E3 = ?
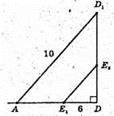
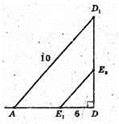
ΔADD1: ∠D = 90°, AD = 6, DD1 = 8.
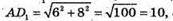
AD1 = 10 см, 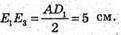
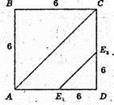
E1E3 = 5 см,
E3E2 = 5 см.
E1E2 = ?
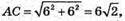
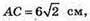
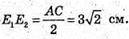
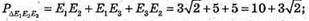
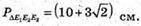
883.
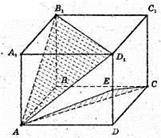
ABCD A1B1C1D1 – прямокутний паралелепіпед. DE = ED1.
Перерізи AB1D1, AEC.
884.
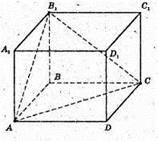
ABCD A1B1C1D1 – куб.
AB = 5 дм.
PΔAB1C = ?
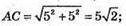
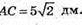
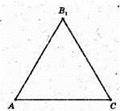
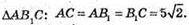
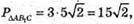
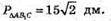
885 .
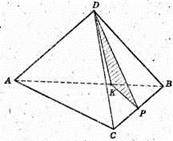
ABCD – правильний тетраедр, AB = 10 см.
АB = KB, CP = PB.
PΔKDP = ?
ΔKDP – переріз,
KP – середня лінія ΔABC.
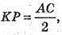 KP = 5 см.
KP = 5 см.
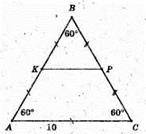
ΔCDP: CD = DB = CB = AB = 10.
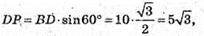
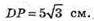
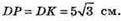
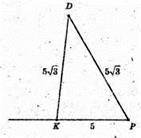
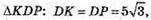
KP = 5.
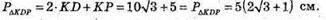
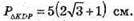
Related posts:
- Геометричні тіла 628. А) спільна вершина; Б) спільне ребро; В) спільна грань; Г) спільна діагональ. 629. А) дві кулі не мають спільних точок; Б) дві кулі мають одну спільну точку; В) дві кулі, які перетинаються; Г) кулі мають різні радіуси і спільний центр. 630. Дано точку О і r > 0, г – відстань. ОХ ≤ r. […]...
- Многогранники 663. А) Грань – Г = 6; ребро – Р = 12; вершина – В = 8. Теорема Ейлера: В – Р + Г; 8 – 12 + 6 = 2. Б) Г = 5; Р = 9; В = 6. 6 – 9 + 5 = 2 В) Г= 7; Р = 12; В […]...
- Геометричні тіла і поверхні 219. Дано: FABCD – піраміда правильна, AB = 6 см, ∠DFC = 60°. 1) Знайти SABCD i висоту FO. SABCD = 62 = 36 (см2). ΔDFC, DF = FC за умовою І ∠DFC = 60° → DF = FC = DC = 6 (см). Відповідь: 36 см2, 2) ∠FCA – ? Відповідь: 3) ∠AFC – […]...
- Прямокутний паралелепіпед – Геометричні фігури й величини Математика – Алгебра Геометричні фігури й величини Прямокутний паралелепіпед Прямокутний паралелепіпед (див. рисунок) має 8 вершин, 12 ребер, котрі можна розбити на 3 групи по 4 рівних, а також 6 граней (3 пари рівних між собою прямокутників). Площа поверхні прямокутного паралелепіпеда дорівнює сумі площ його граней: . Об’єм прямокутного паралелепіпеда . Коли , дістанемо Куб […]...
- Правильні многогранники 862. Якщо у піраміді всі ребра рівні, то з них можна скласти правильний октаедр. АB = а; AM = а; Відповідь: 863. А) так; б) так. 864. А) ні; б) так; в) ні. 865. Якщо з однієї вершини куба провести три діагоналі бічних граней і їх кінці з’єднати відрізками, то утворена піраміда буде тетраедром. 866. […]...
- ПРОСТІ І СКЛАДЕНІ ЗАДАЧІ НА ВИЗНАЧЕННЯ ЧАСУ І ВІДСТАНІ. ГЕОМЕТРИЧНІ ТІЛА ТА ЇХ НАЗВИ Мета: узагальнювати знання учнів про зв’язок між величинами: швидкість, час, відстань; закріплювати вміння розв’язувати задачі на знаходження цих величин, виконувати дії над іменованими числами; ознайомити з назвами геометричних тіл; розвивати мислення; виховувати інтерес до предмета. ХІД УРОКУ І. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. КОНТРОЛЬ, КОРЕКЦІЯ І ЗАКРІПЛЕННЯ ЗНАНЬ 1. Перевірка домашнього завдання 2. Усні обчислення Робота в […]...
- Правильні многокутники Геометрія Многокутники Правильні многокутники Опуклий многокутник називається Правильним, якщо в нього всі сторони рівні й усі кути рівні. Многокутник називається Вписаним у коло, якщо всі його вершини лежать на деякому колі. Многокутник називається Описаним навколо кола, якщо всі його сторони дотикаються до деякого кола. Теорема 1. Правильний опуклий многокутник є вписаним у коло й описаним […]...
- Геометричні тіла та їх назви УРОК 49 Тема. Геометричні тіла та їх назви Мета: ознайомити з назвами геометричних тіл; проаналізувати значення виразів, складених за даною умовою задачі; розвивати логічне мислення. Обладнання: картки для усної лічби, таблиці “Геометричні тіла”, макети геометричних тіл. ХІД УРОКУ I. Контроль і закріплення знань учнів 1. Перевірка домашнього завдання – Прочитати знайдені величини із вправи № […]...
- Геометричні перетворення у просторі. Рухи 306. Пряма і площина відображуються на себе відносно будь-якої точки, що належить їм. 307. Два нерівні відрізки бути симетричними відносно деякої точки не можуть. 308. Відносно початку координат: Точці А(1; -3; 2) симетрична A1(-1; 3;-2); Точці В(-5; 0; 2) – B1(5; 0; -2); Точці С(3; -1; 0) – С1 (-3; 1; 0); Точці D(0; 0; […]...
- Багатогранники. Правильні багатогранники 3. Найменша кількість ребер, що сходиться в одній вершині багатогранника – три. 4. В одній вершині багатогранника може сходитися безліч ребер. Розглянемо піраміду з n-кутником в основі. Яким би великим не було число п, Завжди можна побудувати піраміду, основа якої має n + 1 вершин. 5. Розглянемо трикутну піраміду. Кількість її ребер шість. Шість – […]...
- Прямокутний паралелепіпед. Куб. Піраміда Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 25. Прямокутний паралелепіпед. Куб. Піраміда Сірникова коробочка, цеглина, дерев’яний брусок, ящик, пенал дають уявлення про геометричну фігуру, яка називається прямокутним паралелепіпедом (рис. 188). Рис. 188 Поверхня прямокутного паралелепіпеда складається із шести прямокутників, які називаються його гранями. Протилежні грані прямокутного паралелепіпеда попарно рівні. […]...
- Правильні многокутники УРОК № 17 Тема. Правильні многокутники Мета уроку: формування поняття правильного многокутника, центра і центрального кута правильного многокутника. Формування вмінь застосовувати вивчений матеріал до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: табл. 4. Вимоги до рівня підготовки учнів: формують означення правильного многокутника; застосовують вивчені означення до розв’язування задач. Хід уроку І. Перевірка домашнього завдання […]...
- Тіла і поверхні обертання 905. На рисунку тіло, утворене обертанням прямокутника навколо його сторони. 906. А) Тіло, утворене обертанням прямокутного трикутника навколо катета, Б) Тіло, утворене обертанням прямокутного трикутника навколо гіпотенузи. ΔABC – прямокутний, AB – гіпотенуза. 907. Площина симетрії тіла обертання проходить через його вісь. 908. Див. рис. 909. У площині прямокутника ззовні його і паралельно одній з […]...
- Тіла обертання 1008. Осьовий переріз – це ΔARB1, де BB1 = 2 × СВ = 4 (см), АС + В 1В, В 1C = СB. S = 4 см2. 1009. Sб. ц. = 2πrh = 2π × 2 × 10 = 40π (см2), Sб = 40π см2. 1010. Sб. ц. = 4 × 5 = 20 (см2), […]...
- Геометричні фігури на площині Геометричні фігури на площині – Прямокутник – Квадрат 1 Назви множину. Розбий множину многокутників на підмножини. За якою ознакою це можна зробити? Розбий множину чотирикутників на дві підмножини. Розкажи, що ти знаєш про прямокутник. Розбий множину прямокутників на дві підмножини. Розкажи, що ти знаєш про квадрат. Якою фігурою є ABCD? KMNO? Назви пари протилежних сторін […]...
- Поворот і симетрія відносно прямої 373. Із т. А опустимо перпендикуляр AD + l. Відкладемо ∠ΑΟΛ, = α, А1O + l. Виконано поворот т. А навколо прямої l на кут α. Аналогічно вчинимо з т. В. Відрізок АВ у результаті повороту на кут α навколо прямої l відобразиться у відрізок. 374. Таких поворотів безліч. 375. Точка А(1; 2; 0) відобразиться […]...
- Многокутники. Рівні фігури Розділ I НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ § 2. ДОДАВАННЯ І ВІДНІМАННЯ НАТУРАЛЬНИХ ЧИСЕЛ 13. Многокутники. Рівні фігури На рисунках 107 і 108 зображено три фігури, кожна з яких обмежена замкненою ламаною, що складається з чотирьох ланок: АВ, ВС, CD і DA. Чим відрізняються межі фігур на рисунку 107 від межі фігури на рисунку […]...
- Двогранні кути 520. Нехай дано двогранний кут, міра якого 60°, ∠AOB = 60°. AO + MN, BO + MN, АВ + β, АВ = 12 см. ΔАОВ – прямокутний. 521. Нехай дано двогранний кут, який дорівнює 45°. т. В? α, ОВ = 8 дм. АВ + β. Δ ΟΒΑ – прямокутний. 522. Нехай дано двогранний кут ∠BOA. […]...
- СТЕПІНЬ НАТУРАЛЬНОГО ЧИСЛА З НАТУРАЛЬНИМ ПОКАЗНИКОМ. ПЛОЩІ ТА ОБ’ЄМИ ФІГУР ЗАДАЧІ НА ПОВТОРЕННЯ СТЕПІНЬ НАТУРАЛЬНОГО ЧИСЛА З НАТУРАЛЬНИМ ПОКАЗНИКОМ. ПЛОЩІ ТА ОБ’ЄМИ ФІГУР 50. Обчисліть: 1)5 ∙ 26 + 22 – 4 ∙З4; 3) б2: 2 ∙ (43-55); 2) 2(2 ∙ 53- 102): 52; 4) 23: 12 ∙ 53-(32 ∙ 5-5). 51. Знайдіть значення виразу а3+ b2, якщо: 1) а = 2, b= 12; 2)а=1,b=1; […]...
- Многокутники. Розв’язування задач Урок № 49 Тема: Многокутники. Розв’язування задач Мета. Формувати в учнів уміння і навички самостійно застосовувати вивчений матеріал, до розв’язування задач, розвивати навички самостійної пізнавальної роботи, розвивати вміння самостійної роботи, розвивати вміння аналізувати, робити висновки. Форми роботи: математичний диктант, бесіда, розв’язування задач і виконання вправ. Обладнання: лінійка, кольорова крейда, косинець. Тип уроку: урок узагальнення і […]...
- Заключний урок з теми “Геометричні побудови” Урок № 51 Тема. Заключний урок з теми “Геометричні побудови” Мета: систематизувати та узагальнити знання учнів, набуті в ході вивчення теми “Геометричні побудови”. Систематизувати та узагальнити вміння учнів розв’язувати задачі: – на застосування означення та властивостей кола і його елементів; – на побудову за допомогою циркуля та лінійки; – на метод застосування означення та властивостей […]...
- Многокутники Геометрія Многокутники Ламаною … називається фігура, яка складається з точок , , ,…, і відрізків, що їх послідовно сполучають. Точки , , , …, називаються Вершинами ламаної, а відрізки ; ; …; – Ланками ламаної. Ламана називається Простою, якщо вона не має самоперетинів. Довжиною ламаної називається сума довжин її ланок. На рисунку 1 зображена проста […]...
- ГЕОМЕТРИЧНІ ПОБУДОВИ РОЗДІЛ 4 КОЛО І КРУГ. ГЕОМЕТРИЧНІ ПОБУДОВИ & 18. ГЕОМЕТРИЧНІ ПОБУДОВИ Користуючись лінійкою1 і циркулем, можна виконувати багато геометричних побудову тобто креслити геометричні фігури. Розглянемо спочатку, як виконувати найпростіші геометричні побудови. ЗАДАЧА 1 Побудуйте трикутник із даними сторонами. РОЗВ’ЯЗАННЯ. Нехай дано три відрізки: а, b і с (мал. 224). Треба побудувати трикутник, сторони якого дорівнювали […]...
- Піраміди 937. SΔABC = 30 см2. 938. ΔFMO: ∠О = 90°, OF = 4 см, ОМ = 3 см, FM = 5 см. 939. Δ ΟΡΕ: Ο = 90°, ∠Ε = 60°, ∠ΟΡΕ = 30°, ΡΕ = 10. ΟΕ = 5. DC = 2ΟΕ = 10, DC = 10. SABCD = 102= 100 (см2). 940. ΔOPE: […]...
- РУХ ТІЛА, КИНУТОГО ГОРИЗОНТАЛЬНО – РУХ ТІЛА В БЕЗПОВІТРЯНОМУ ПРОСТОРІ (БЕЗ УРАХУВАННЯ СИЛИ ТЕРТЯ) Фізика підготовка до ЗНО комплексне видання МЕХАНІКА 2. ОСНОВИ ДИНАМІКИ 2.3. РУХ ТІЛА В БЕЗПОВІТРЯНОМУ ПРОСТОРІ (БЕЗ УРАХУВАННЯ СИЛИ ТЕРТЯ) 2.3.1. РУХ ТІЛА, КИНУТОГО ГОРИЗОНТАЛЬНО Тіло, кинуте горизонтально, рухається по параболічній траєкторії: його рух складається із руху горизонтального зі сталою швидкістю 0 і вільного падіння з нульовою початковою швидкістю. На рис. 37 зображено рух тіла, […]...
- ВАГА ТІЛА. ВАГА ТІЛА, ЯКЕ РУХАЄТЬСЯ З ПРИСКОРЕННЯМ. ПЕРЕВАНТАЖЕННЯ. НЕВАГОМІСТЬ – СИЛИ В МЕХАНІЦІ Фізика підготовка до ЗНО комплексне видання МЕХАНІКА 2. ОСНОВИ ДИНАМІКИ 2.2. СИЛИ В МЕХАНІЦІ 2.2.4. ВАГА ТІЛА. ВАГА ТІЛА, ЯКЕ РУХАЄТЬСЯ З ПРИСКОРЕННЯМ. ПЕРЕВАНТАЖЕННЯ. НЕВАГОМІСТЬ Вага тіла – це сила, з якою тіло діє на опору чи підвіс унаслідок притягання його до Землі. Якщо опора перебуває в спокої або рухається рівномірно і прямолінійно, то вага […]...
- Прямокутний паралелепіпед. Піраміда Розділ I НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ § 3. МНОЖЕННЯ І ДІЛЕННЯ НАТУРАЛЬНИХ ЧИСЕЛ 22. Прямокутний паралелепіпед. Піраміда Рис. 153 Коли ви були маленькими і гралися кубиками, то, можливо, складали фігури, зображені на рисунку 153. Ці фігури дають уявлення про прямокутний паралелепіпед. Форму прямокутного паралелепіпеда мають, наприклад, коробка цукерок, книга, цеглина, коробка сірників, пакувальний […]...
- Геометричні побудови Урок № 52 Тема. Геометричні побудови Мета: продіагностувати рівень засвоєння учнями знань та вмінь, передбачений програмою під час вивчення теми “Геометричні побудови”. Тип уроку: перевірка і корекція знань, умінь та навичок. ХІД УРОКУ І. Організаційний момент ІІ. Перевірка домашнього завдання Зібрати зошити з домашньою контрольною роботою ІІІ. Умова контрольної роботи Варіант 1 Початковий рівень 1. […]...
- Комбінації тіл 1073. Нехай ABCDA1B1C1D1 – куб, вписаний в кулю з центром О, B1O = OD = 8 см. Тоді B1D = 2В1О = 2 × 8 = 16 (см). Відповідь: 16 см. 1074. Див. рис. 1075. Див. рис. 1076. Див. рис. 1077. Див. рис. 1078. Див. рис. 1079. Нехай ABCA1B1C1 – правильна трикутна призма. Sбіч. = […]...
- Многогранні кути 607. Правильний октаедр має 8 граней, кожна з яких – правильний трикутник. Він має 6 чотиригранних кутів. 608. Чотиригранний кут 40°; 70°; 110° і 140° існує неопуклий. 609. Якщо всі плоскі кути чотиригранного кута рівні, то кожний його двогранний кут дорівнює протилежному (октаедр). Площини, які проходять через його протилежні ребра, – перпендикулярні. 611. Якщо у […]...