Графік функції
Урок № 63
Тема. Графік функції
Мета: формувати вміння виконувати побудову графіка функції, заданої формулою “по точках”; відпрацьовувати навички “читання” графіків функцій; провести діагностику засвоєння матеріалу з теми “Функція. Графік функції”.
Хід уроку
I. Організаційний момент
Вступне слово вчителя. Перевірка готовності учнів до уроку; місце уроку в темі, план роботи на уроці.
II. Перевірка домашнього завдання
@ Одна із можливих форм проведення цього етапу уроку – взаємоперевірка за зразком:
III. Формулювання мети й завдань уроку
Мотивація навчальної діяльності
@ Щоб учні усвідомили необхідність опанування навчальною матеріалу уроку (оволодіння вміннями будувати графік функції, заданої формулою, та відпрацювання навичок роботи з побудованим графіком функції) можна запропонувати задачу. Функцію задано формулою у = 4 – х2, де -3 ? х? 3. При яких значеннях х
Проблема (протиріччя), що виникає в ході розв’язування задачі (якщо був би графік – розв’язали б), спонукає учнів до усвідомлення того факту, що не достатньо вміти працювати із готовим графіком функції, треба навчитися використовувати здобуті в цій темі знання для того, щоб навчитися самим будувати графік функції.
IV. Актуалізація опорних знань
Виконання усних вправ
1. Відшукайте область визначення функції, яку задано формулою:
1) у = 2х; 2) у = 3х + 4; 3) 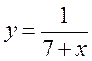 .
.
2. Функцію задано формулою 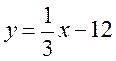 .
.
Знайдіть:
1) значення функції, що відповідає значенню аргументу 0; -3; 24;
2) при якому значенні аргументу функція набуває значення 0; -1;
3) чи належить графіку функції точка А(3; -11);
4) яку абсцису має точка М, що лежить на графіку, якщо ордината і очки М дорівнює 2?
V. Вивчення нового матеріалу
@ Оскільки методика побудови графіка функції за точками, що опановується учнями на цьому уроці, базується на понятті неперервності функції (яке використовується на інтуїтивному рівні), бажано перед поясненнями щодо способу побудови графіка, звернутись ще раз до готових графіків і акцентувати учнів на тому факті, що розглянуті графіки функцій: а) по-перше, складаються з точок, що щільно “стоять одна біля одної”; б) по-друге, перехід від однієї точки до іншої настільки непомітний, “плавний”, тому лінії, що представляють графіки, є або плавними кривими, або частинами прямих (відрізками, променями і т. д ).
Тому, якщо б ми хотіли “скопіювати” будь-який з таких готових графіків, то ми б, напевно, не “копіювали” всі точки (бо це неможливо), а перенесли лише деякі “ключові” з них, а потім, провівши через здобуті “ключові” точки плавні криві лінії або частини прямих (залежно від умови завдання), “перенесли” всі інші точки.
Тільки після приблизно таких вступних слів, учні можуть зрозуміти запропоновану методику.
Покажемо, як можна побудувати графік функції, яку задано формулою.
Нехай функцію задано формулою у = х(6 – х), де -1 ? х? 5.
Складемо таблицю деяких відповідних значень аргументу й функції:
Х | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
У | -7 | 0 | 5 | 8 | 9 | 8 | 5 |
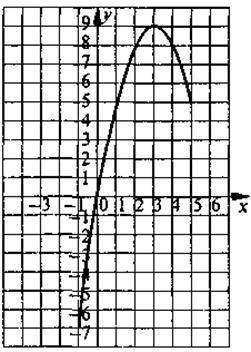
Позначимо на координатній площині точки, координати яких указано в таблиці. З’єднаємо їх плавною лінією (рис.) Дістанемо графік функції, заданої формулою у = х(6 – х), де -1 ? х? 5. Чим більше позначимо точок, що належать графіку, і чим щільніше вони будуть розташовані, тим точніше буде побудовано графік функції.
VI. Закріплення знань учнів. Відпрацювання навичок
Виконання письмових вправ
1. Побудуйте графік функції, яку задано формулою:
1) у = x2 + 2x, -3 ? x? 2;
2) 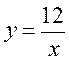 , де 1 ? х? 12;
, де 1 ? х? 12;
3) у = 5 – х, де -4 ? х? 6.
2. Графіком функції є ламана ABCD, причому А(-2; -3); В(0; 3); С(4; 3);
D (6; 1). Накресліть графік функції та заповніть таблицю.
Х | -1 | 1,33 | 4,5 |
У | -2 | 3 | 1,5 |
Яка область визначення та область значень функції?
VII. Підсумки уроку
Тестове завдання
1. Функцію задано формулою у = х2 + 2х – 3. Обчисліть її значення при х = -2.
1) -11; 2) 5; 3) -3; 4) 11.
2. Функцію задано формулою у = 3х – 5. При якому значенні аргументу функція дорівнює 10?
1) -5; 2) 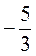 ; 3)
; 3) 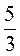 ; 4) 5.
; 4) 5.
3. Знайдіть область визначення функції 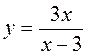 .
.
1) х? -3; 2) х? 3; 3) х? 0; 4) х – будь-яке число.
4. Які з даних точок: М(3; 2), N(-4; -3,4), D(-2; -2), 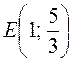 – належать графіку функції
– належать графіку функції 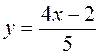 ?
?
1) М; N; D; 2) М; D; Е; 3) М; D; 4) М; N; D; Е.
5. Функцію задано формулою у = – х +2 (-3 ? х? 2). Який із графіків є графіком цієї функції?
1) А; 2) Б; 3) В; 4) Г.
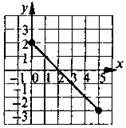
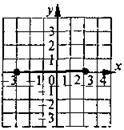
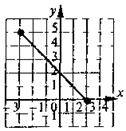
А
Б
В
Г
VIII. Домашнє завдання
№ 1. Графіком функції є ламана KLMN, причому К(-4; 4), L(-2; 2), М(2; 7), N(3; 3). Накресліть графік функції та заповніть таблицю:
Х | -3 | 1,25 | 2,5 |
У | 3,5 | 2 | 3 |
Яка область визначення та область значень функції?
№ 2. Побудуйте графік функції, заданої формулою, склавши попередньо таблицю значень із кроком 1. Порівняйте рівняння функції та графіка (за видом функції та видом графіка). Які висновки ви можете зробити?
1) у = -2х, 3,0 ? x? 4; 2) у = – x + 5, 1 ? x? 5; 3) 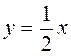 , -2 ? х? 2;
, -2 ? х? 2;
4) 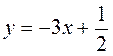 , 0 ? х? 3.
, 0 ? х? 3.
