Головна ⇒ 📌Фізика ⇒ ГРАФІКИ РІВНОМІРНОГО РУХУ

ГРАФІКИ РІВНОМІРНОГО РУХУ

Розділ 2 МЕХАНІЧНИЙ РУХ

& 10. ГРАФІКИ РІВНОМІРНОГО РУХУ
Спортсмен, велосипед якого має спідометр, рухається по трасі (рис. 10.1). Швидкість руху, яку показує спідометр у будь-який момент часу, дорівнює 5 м/с. Як описати рух цього спортсмена і взагалі будь-якого тіла за допомогою графіків? Згадаємо, адже графіки руху тіл ви вивчали в курсі математики 6 класу.
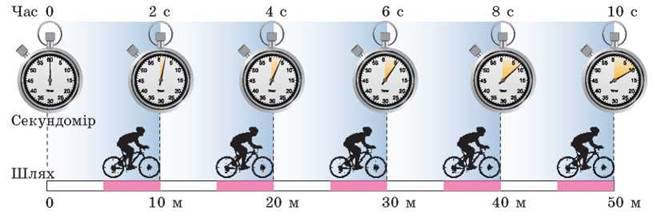
Рис. 10.1. Велосипедист рухається рівномірно: за будь-які рівні інтервали часу він долає однаковий шлях
1. Будуємо графік залежності шляху від часу

для рівномірного руху тіла
Побудуємо графік залежності шляху, що долає велосипедист (див. рис. 10.1), від часу спостереження – графік шляху.
Для побудови графіка виконаємо такі дії.
1. Заповнимо таблицю відповідних значень часу t руху спортсмена та шляху l, який він долає за цей час.
Зрозуміло, що в момент початку спостереження (t = 0) шлях теж дорівнює нулю (l = 0). За час t = 2 c велосипедист подолає відстань 10 м: l = v ∙ t = 5 ∙ 2с = 10м. Міркуючи аналогічно, отримаємо: с
T, с
0
2
4
6
8
10
L, м
0
10
20
30
40
50
2.

Проведемо дві взаємно перпендикулярні осі.
На горизонтальній осі – осі абсцис – відкладемо час руху велосипедиста в секундах (t, с) так, що одній клітинці відповідатиме інтервал часу 2 с. На вертикальній осі – осі ординат – відкладемо шлях у метрах (l, м) так, що одній клітинці відповідатиме шлях, який дорівнює 10 м (рис. 10.2, а).
3. Побудуємо точки з координатами: (0; 0), (2; 10), (4; 20), (6; 30), (8; 40), (10; 50).
Абсциси зазначених точок відповідають часу руху спортсмена, ординати – шляху, який він подолав за цей час (рис. 10.2, б).
4. З’єднаємо побудовані точки лінією (рис. 10.2, в). Отриманий відрізок прямої – графік шляху велосипедиста.
Зверніть увагу! Велосипедист рухається рівномірно, тому шлях, який він долає, можна визначити за формулою l = vt, у будь-який момент часу v = 5 м/с; тому можна записати: l= 5t(м), де час t задано в секундах. Рівність l = 5t – рівняння залежності шляху, який долає велосипедист, від часу спостереження.
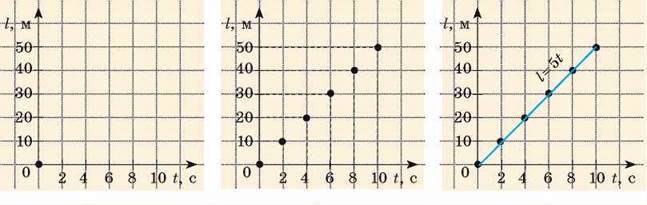
А б в
Рис. 10.2. Побудова графіка шляху велосипедиста, який рівномірно рухається зі швидкістю v = 5 м/с
У разі рівномірного руху графік шляху – це завжди відрізок прямої, нахиленої під певним кутом до осі часу. Тому для побудови графіка шляху достатньо знайти шлях l для двох значень часу t і через отримані дві точки провести відрізок прямої. Наприклад, будуючи графік шляху велосипедиста, слід узяти час початку спостереження (t = 0) і час закінчення спостереження (t = 10 с) (рис. 10.3).
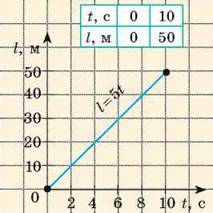
Рис. 10.3. Графік шляху для тіла, яке рухається з незмінною швидкістю 5 м/с
2. З’ясовуємо, про що можна дізнатися за графіком шляху
Графік шляху дає багато корисної інформації. За графіком шляху можна:
1) дізнатися про характер руху тіла;
2) визначити шлях, який долає тіло за певний інтервал часу;
3) визначити швидкість руху тіла;
4) порівняти швидкості руху тіл: чим більша швидкість руху тіла, тим більший кут між графіком шляху та віссю часу (рис. 10.4).
Розглянемо приклад.
Задача. За графіком шляху, який подолало тіло за 4 години (рис. 10.5), дізнайтеся: 1) як рухалось тіло; 2) який шлях подолало тіло за першу годину; за наступні дві години; 3) якою була швидкість руху тіла на кожній ділянці.
Розв’язання
Із графіка бачимо, що весь шлях складається з трьох ділянок, на кожній з яких тіло рухалось рівномірно (графік шляху тіла – відрізки прямих).
Ділянка I. За графіком шлях, який подолало тіло за першу годину, дорівнює 20 км, тому швидкість руху тіла становила:
VI = 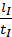= = 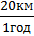20 .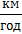
Ділянка ІІ. За наступні 2 години тіло подолало шлях l11 = 30 км – 20 км = 10 км. Відповідно швидкість руху тіла дорівнювала:
VII = 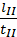= = 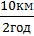5 .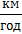
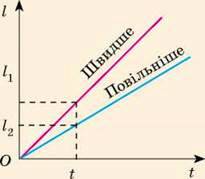
Рис. 10.4. За той самий час тіло, яке має більшу швидкість руху, долає більший шлях (l1 >l2)
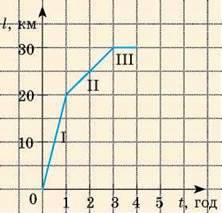
Рис. 10.5. До задачі в & 10
Ділянка ІІІ. Останню годину шлях не змінювався, отже, тіло зупинилось: lIII = 30км – 30км = 0; v = 0.
Аналіз результатів. Із графіка бачимо, що ділянка I графіка складає з віссю часу більший кут, ніж ділянка ІІ. Тому ділянка І відповідає більшій швидкості руху тіла. Результат є цілком реальним.
3. Будуємо графік швидкості рівномірного руху тіла
Повернемося до велосипедиста, який рухається рівномірно зі швидкістю v = 5 м/с (див. рис. 10.1). Побудуємо графік залежності швидкості його руху від часу спостереження – графік швидкості руху.
Для побудови графіка виконаємо таки дії.
1. Заповнимо таблицю відповідних моментів часу t руху спортсмена та швидкості руху v, яку він мав у ці моменти часу:
T, с
0
2
4
6
8
10
V, м/с
5
5
5
5
5
5
Спортсмен рухався рівномірно, тому швидкість його руху залишалась незмінною протягом усього часу спостереження.
2. Проведемо дві взаємно перпендикулярні осі. На осі абсцис відкладемо час руху в секундах (t, с), на осі ординат – швидкість руху в метрах за секунду (v, ) (рис. 10.6).
3. Побудуємо точки з координатами (0; 5), (2; 5), (4; 5), (6; 5), (8; 5), (10; 5). Абсциси позначених точок відповідають часу руху спортсмена, ординати – швидкості його руху.
4. З’єднаємо точки лінією. Отриманий відрізок прямої – графік швидкості руху велосипедиста.
У разі рівномірного руху графік швидкості руху тіла – відрізок прямої, паралельної осі часу.
Рис. 10.6. Графік швидкості руху велосипедиста, який рухається рівномірно зі швидкістю v = 5 м/с. Час спостереження t = 10 с
4. З’ясовуємо, про що можна дізнатися за графіком швидкості руху тіла
Розглянемо графік швидкості руху деякого тіла (рис. 10.7, а) і дізнаємося про його рух якнайбільше.
1. Протягом інтервалу часу від 0 до 5 с і протягом інтервалу часу від 5 до 15 с тіло рухалось рівномірно, оскільки графік швидкості руху – відрізки прямих, які паралельні вісі часу.
2. Швидкість руху тіла протягом останніх 10 с спостереження більша, ніж протягом перших 5 с, оскільки друга ділянка графіка розташована вище від осі часу, ніж перша ділянка (рис. 10.7, б).
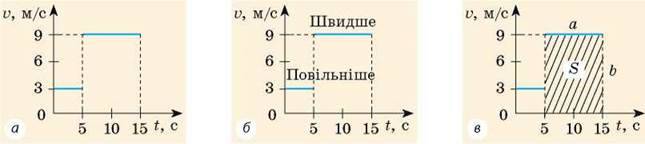
Рис. 10.7. Дослідження графіка швидкості руху тіла
У даному випадку:
V1 = 3 – на інтервалі часу від 0 до 5 с;
V2 = 9 – на інтервалі часу від 5 до 15 с.
3. Можна визначити шлях l, який подолало тіло (згадайте: l = vt). Наприклад, за інтервал часу від 5 до 15 с тіло подолало шлях 90 м:
L2 = v2t2 = 9 ∙ (5 с – 5с) = 90 м.
Цей шлях чисельно дорівнює площі заштрихованого прямокутника (рис. 10.7, в):
S = a ∙ b = 10 ∙ 9 = 90; l = 90 м.
Зверніть увагу! Для будь-якого руху числове значення шляху, який подолало тіло, дорівнює числовому значенню площі фігури під графіком швидкості руху цього тіла.
Підбиваємо підсумки
У разі рівномірного руху тіла графік шляху – це завжди відрізок прямої, нахиленої під певним кутом до осі часу, а графік швидкості руху – це відрізок прямої, паралельної осі часу.
За графіком шляху можна: 1) дізнатися, як рухалось тіло; 2) знайти шлях, який долало тіло за певний інтервал часу; 3) визначити та порівняти швидкості руху тіл: чим більша швидкість руху тіла, тим більший кут між графіком шляху та віссю часу.
За графіком швидкості руху можна: 1) дізнатися, як рухалось тіло; 2) знайти шлях, який долало тіло за певний інтервал часу; 3) визначити та порівняти швидкості руху тіл: чим більша швидкість руху тіла, тім вище від осі часу розташований графік швидкості руху.
Контрольні запитання
1. Який вигляд має графік шляху в разі рівномірного руху? 2. Як за графіками шляхів двох тіл порівняти їхні швидкості руху? 3. Який вигляд має графік швидкості рівномірного руху тіла? 4. Як за графіками швидкостей двох тіл порівняти їхні швидкості руху? 5. Як за графіком швидкості руху тіла визначити шлях, подоланий тілом?
Вправа № 10
1. За поданими на рис. 1 графіками швидкості руху трьох тіл з’ясуйте, як рухались ці тіла; яке тіло рухалося найшвидше.
2. Ягуар, наздоганяючи здобич, може короткий час рухатися зі швидкістю 25 м/с. Побудуйте графік швидкості руху ягуара за 5 с спостереження. Покажіть на графіку шлях, який долає ягуар за цей час, і визначте цей шлях.
3. На рис. 2 зображені графіки шляхів для пішохода, велосипедиста й трактора, які рухаються зі швидкостями 4, 12 і 24 км/год відповідно. Який із зображених графіків якому тілу відповідає? Побудуйте графіки швидкості руху зазначених тіл.
4. Розгляньте графік польоту орла (рис. 3) і визначте: а) який шлях подолав орел за час спостереження; б) скільки часу орел відпочивав; в) яку відстань подолав орел за перші 25 с спостереження. Побудуйте графік швидкості руху орла.
5. Розгляньте графік швидкості руху тіла (рис. 4) і дізнайтесь: а) як рухалось тіло; б) якою була швидкість руху тіла на кожній ділянці; в) який шлях подолало тіло. Побудуйте графік шляху цього тіла.
6. Придумайте графічну задачу на рух із життя ваших улюблених героїв мультфільмів, розв’яжіть її та оформте на окремому аркуші.
7. Із рівняння v = 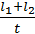знайдіть:
А) v, якщо l1= 15 м, l2 = 20 м, t = 10 с;
Б) t, якщо l1 = 1 км, l2 = 9 км, v = 4 км/год;
В) l1 якщо l2 = 100 м, t = 5 хв, v = 25 м/хв.
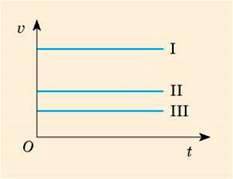
Рис. 1
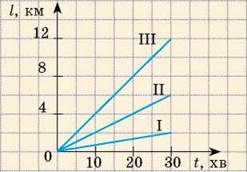
Рис. 2
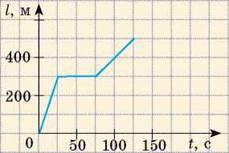
Рис. 3
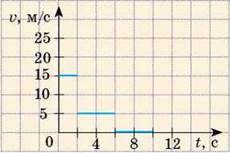
Рис. 4

1 Звезда

2 Звезды

3 Звезды

4 Звезды

5 Звезд

(1 votes, average: 5.00 out of 5)

Loading...

Ви зараз читаєте: ГРАФІКИ РІВНОМІРНОГО РУХУ

« Географічне положення Північної Америки. Історія відкриття та освоєння

ПРАВИЛА БЕЗПЕЧНОЇ ПОВЕДІНКИ НА ВУЛИЦІ. ЯК ЗНАЙТИ ВИХІД З НЕПЕРЕДБАЧЕНИХ СИТУАЦІЙ »