Лінійне рівняння з однією змінною. Розв’язування лінійних рівнянь з однією змінною і рівнянь, що зводяться до них
Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ
& 23. Лінійне рівняння з однією змінною. Розв’язування лінійних рівнянь з однією змінною і рівнянь, що зводяться до них
Ми знаємо, як розв’язувати рівняння 2х = -8;  х – 5; 0,01х -17.
х – 5; 0,01х -17.
Кожне із цих рівнянь має вигляд ах = b, де х – змінна, а і b – деякі числа.
Числа а і b називають коефіцієнтами рівняння.
Якщо а ≠ 0, то рівняння ах = b називають рівнянням першого степеня з однією змінною. Поділивши обидві частини такого рівняння на а, одержимо х = 
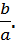
Якщо а – 0 і b – 0, то лінійне рівняння має вигляд 0х – 0. Коренем такого рівняння є будь-яке число, оскільки при будь – якому значенні х значення лівої і правої частин рівняння є рівні і дорівнюють нулю. Тому рівняння 0х = 0 має безліч коренів.
Якщо а – 0, а b ≠ 0, то лінійне рівняння матиме вигляд 0х – b. При цьому не існує жодного значення змінної х, яке б перетворювало ліву і праву частини рівняння на одне й те саме число. Адже значення лівої частини рівняння при будь-якому значенні х дорівнюватиме нулю, а значення правої частини
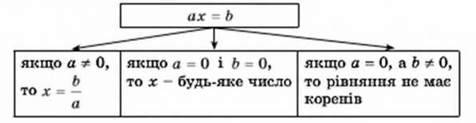
Систематизуємо дані про розв’язки лінійного рівняння ах = b у вигляді схеми:
Приклад 1. Розв’язати рівняння:
1) 0,2х = 7;
2)-  Х = 2-;
Х = 2-;
3) 0х = 7.
Р о з в ‘ я з а н н я.
1) 0,2х = 7; х = 7 : 0,2; х = 35.
Відповідь: 35.
2) –  Х = 2
Х = 2  ;
;
Х = 2  : ( –
: ( –  );
);
Х = -4.
Відповідь: – 4.
3)0х = 7; рівняння не має коренів.
Відповідь: коренів не має.
Процес розв’язування багатьох рівнянь є зведенням цих рівнянь до лілійних шляхом рівносильних перетворень за властивостями рівнянь.
Приклад 2. Розв’язати рівняння:
1) 3(х + 1) – 2х = 6 – 4х;
2) 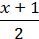 +
+ 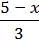 =
= 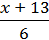 .
.
Р о з в ‘ я з а н н я.
1. Позбудемося знаменників (якщо вони є):
1)3(х + 3) – 2х = 6 – 4х.
2) 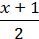 +
+ 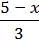 =
= 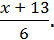
Помножимо обидві частили рівняння на 6 (6 – найменший спільний знаменник дробів). Маємо:
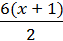 +
+ 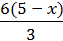 =
= 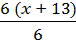
3(х + 1) + 2(5 – х) = х + 13.
2. Розкриємо дужки (якщо вони є):
3х + 9 – 2х = 6 – 4х;
3х + 3 + 10 – 2х = х + 13.
3. Перенесемо доданки, що містять змінну, у ліву частину, а інші – у праву, змінивши знаки цих доданків, на протилежні:
3х – 2х + 4х = 6 – 9;
3х – 2х – х = 13 – 3 – 10.
4. Зведемо подібні доданки:
5х = – 3;
0х = 0.
5. Розв’яжемо отримане лінійне рівняння:
Х = -3 : 5;
Х = -0,6;
Відповідь: -0,6.
Х – будь-яке число.
Відповідь: будь-яке число.
Приклад 3. Розв’язати рівняння 5(х + р) = 3х – 7р відносно х.
Р о з в ‘ я з а н н я. Розкриємо дужки в лівій частині рівняння: 5х + 5р – 3х – 7р. Перенесемо доданок 3х у ліву частину, а 5р – у праву. Маємо: 5х – 3х = -7р – 5р; 2х = -12р. Тоді х = (-12р) : 2; х = (-12 : 2)р; х = -6р.
Відповідь: -6р.
Яке рівняння називають лінійним рівнянням з однією змінною? Наведіть приклади лінійних рівнянь. У якому випадку рівняння ах – b має єдиний корінь? У якому випадку коренем рівняння ах – b є будь-яке число? У якому випадку рівняння ах = b не має коренів?
848. (Усно) Яке з рівнянь є лінійним:
1)17х = 0;
2) -5х = –  ;
;
3) х2 = 7х;
4) 0х = 17;
5) х + 7 = х2;
6) 0х = 0?
849. (Усно) Скільки коренів має рівняння:
1) 2х = -7;
2) 0х = 5;
3) 0х = 0?
850. З’ясуйте, яке з даних рівнянь має лише один розв’язок, не має розв’язків, має безліч розв’язків:
1) -5х = -3;
2) 0х = 0;
3) 0,14х = 0;
4) 7 = 0х;
5)  = -5;
= -5;
6) 0х =-15.
851. (Усно) Розв’яжіть рівняння:
1) -2х = 12;
2) 0,5х = -2,5;
3) -2,5х = 7,5;
4)  Х =
Х = 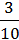 ;
;
5)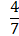 х = 1;
х = 1;
6)5х = -12.
852. Розв’яжіть рівняння:
1) – 3х = -21;
2) -2х =  ;
;
3) –  Х = -5;
Х = -5;
4) 50х = 5;
5) – х = 1  ;
;
6) -0,01х = 0,17;
7) – х = – 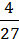 ;
;
8)-1,2х = -4,2;
9)  х = 0.
х = 0.
853. Знайдіть корінь рівняння:
1) 2х = -8;
2)  Х = 9;
Х = 9;
3) -3х =  ;
;
4) -10х = -5;
5) 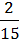 х = 0;
х = 0;
6) 0,1х = 0,18.
854. Визначте, що має бути записано праворуч у рівнянні замість пропусків, якщо відомо його корінь:
1) 8х = … ;
Х = -9;
2) -9х = … ;
Х = 0;
3)  Х = … ;
Х = … ;
Х = 12.
855. Знайдіть корінь рівняння:
1) 7х + 14 = 0;
2) 0, 3х – 21 = 0,5х – 23;
3) 1х + 3 = 6х – 13;
4) 5х + (3х – 7) = 9;
5) 47 = 10 – (9х + 2);
6) (3х + 2) – (8х + 6) = 14.
856. Розв’яжіть рівняння:
1)2х -10 = 0;
2) 1,4х – 12 = 0,9х + 4;
3) 3х + 14 = 5х – 16;
4) 12 – (5х + 10) = -3;
5) 6 – (8х + 11) = -1;
6) (3х – 4) – (6 – 4х) = 4.
857. Яке з рівнянь рівносильне рівнянню 5х = 10:
1) х + 3 = 5;
2) 5 – х = 7;
3) х + 2 = х + 1;
4) х – 7 = -5;
5) х = 8 – 3х;
6)1х – 7 = 4х?
858. Чи є рівняння рівносильними:
1) 4х – х = 17 і 3х = 17;
2) 5х – 9 = 3х і 6х = 21;
3) 2х = -12 і х + 6 = 0;
4) 12х = 0 і 15х = 15?
859. При якому значенні х значення виразу:
1) 3х + 7 дорівнює -2;
2) 4(х + 1) дорівнює значенню виразу 5х – 9?
860. При якому значенні у:
1) значення виразу 5у – 13 дорівнює -3;
2) значення виразів 3(у – 2) і 13у – 8 рівні між собою?
861. Розв’яжіть рівняння:
1) х +  = 5;
= 5;
2) 2х –  = 1;
= 1;
3)  +
+  = 8;
= 8;
4)  –
–  = 1.
= 1.
862. Знайдіть корінь рівняння:
1) х –  = 1;
= 1;
2) 3х +  = 4;
= 4;
2)  –
–  = 1;
= 1;
4)  +
+  = 10.
= 10.
863. Складіть лінійне рівняння, коренем якого є:
1) число -2;
2) число -0,2.
864. Складіть лінійне рівняння:
1) яке не має коренів;
2) коренем якого є будь-яке число.
865. Складіть лінійне рівняння, коренем якого було б:
1) число -8;
2) будь-яке число.
866. Знайдіть корінь рівняння:
1)(4х – 2) + (5х – 4) – 9 – (5 – 11х);
2) (7 – 8х) – (9 – 12х) – (5х + 4) = -16;
3) 3(4х – 5) – 10(2х – 1) = 33;
4) 9(3(х + 1) 2х) = 7(х + 1).
867. Розв’яжіть рівняння:
1) (9х – 4) + (15х – 5) = 18 – (25 – 22х);
2) (10х + 6) – (9 – 9х) + (8 – 11х) = -19;
3) 7(х – 1) – 3(2х + 1) = – х – 15;
4) 5(4(х – 1) – 3х) = 9х.
868. Розв’яжіть рівняння відносно х:
1) 2х + а = х + а;
2) b + х = с – х;
3) 6х + 2m = х – 8m;
4) 9а + х = 3b – 2х.
Р о з в ‘ я з а н н я.
4) 9a – х = 3b – 2х; х + 2х = 3b – 9а; 3х = 3(b – 3а). Поділимо обидві частини рівняння на 3. Одержимо: х = b – 3а.
Відповідь: b – 3а.
869. Розв’яжіть рівняння відносно х:
1) 7х + m = 2х + m;
2) а + х = 2m – х;
3) 3х + b = 9b – х;
4) 5р + 2х = 10а – 3х.
870. Чи є рівносильними рівняння:
1) 2х – 4 = 2 і 5(х – 3) + 1 = 3х – 8;
2) 5х + 3 = 8 і 7(х – 2) + 20 = 4х + 3;
3) 5х = 0 і 0 х = 5;
4) 7х + 1 = 7х 2 і 5(х + 1) = 5х + 5;
5) 0 : х = 7 і 0 ∙ х = 7;
6) 3(х – 2) = 3х – 6 і 2(х + 7) – 2(х + 1) + 12?
871. При якому значенні у значення виразу:
1) 5у + 7 утричі більше за значення виразу у + 5;
2) 2у – 4 на 7,4 більше за значення виразу 3 – 7у?
872. При якому значенні х значення виразу:
1) 7х + 8 удвічі більше за значення виразу х + 7;
2) 5х – 8 па 17,2 менше від значення виразу х + 2 ?
873. Складіть рівняння, яке було б рівносильним рівнянню 7(2х – 8) = 5(7х – 8) – 15х.
874. При якому значенні а рівняння:
1) 2ах = 16 має корінь, що дорівнює 4;
2) 3х – а має корінь, що дорівнює  ;
;
3) 5(а + 1)х = 40 має корінь, що дорівнює -1 ?
875. При якому значенні b коренем рівняння:
1) 3bх = -24 є число -4;
2) (2а – 5)х = 45 с число 3?
876. Розв’яжіть рівняння:
1) 4х + 7 = 3(х – 2) + х:
2) 2х + 5 – 2(х – 4) + 13;
3) 2х(1 – 3х) + 5х(3 – х) = 17х – 8х2;
4) (7х3 + 2х2 – 4х – 5) – (6х3 – х2 + 2х) = 3х2 – (6х – х3).
877. Знайдіть корінь рівняння:
1) 3(х – 2) + 4х = 7(х -1) + 1;
2) 2(х + 1) + х = 6(х + 3);
3) 3х(2 + х) – 4 (1 – х2) = 7х2 + 6х;
4) (х2 + 4х – 8) – (7х – 2х2 – 5) = 3х2 – (3х + 3).
878. Розв’яжіть рівняння:
1) 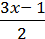 +
+ 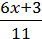 = 10
= 10
2) 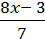 –
– 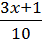 = 2
= 2
3)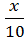 +
+ 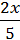 =
= 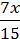 +
+ 
4) 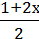 –
– 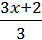 =
= 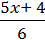
879. Знайдіть корінь рівняння:
1) 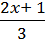 +
+ 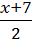 = 5
= 5
2) 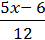 –
– 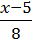 = 1
= 1
3)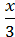 +
+ 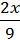 =
= 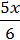 +
+ 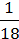
4) 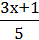 –
– 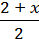 =
= 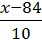
880. Розв’яжіть рівняння:
1) 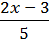 –
– 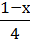 +
+ 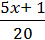 =
= 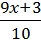
2) х2 – 5х + 3 – 6х2 – 30х +  =
=  .
.
881. Розв’яжіть рівняння:
1) 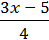 –
– 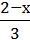 +
+ 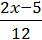 =
= 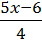
2) х2 – 7х + 4 – 4х2 – 28х + 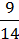 =
= 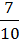 .
.
882. При якому значенні b рівняння мають однакові корені:
1) 4х – 3 = 5 і 3х + b = 17;
2) х + 6 = 9 і 2х – b = х?
883. Розв’яжіть рівняння:
1) 2(|х| – 3) = |х);
2) |2х +1| = 7.
884. Розв’яжіть рівняння:
1)|х + 1| = 0,2;
2) 2(|х| – 3 ) = |х|).
885. Знайдіть усі цілі значення m, при яких корінь рівняння mх = 4 є цілим числом.
886. Знайдіть усі цілі значення b, при яких корінь рівняння bх – -6 є натуральним числом.
Вправи для повторення
887. Тетянка на канікулах розв’язала х задач з математики, а її однокласник Ігор – на 18 задач більше. Виразіть через х кількість задач, які розв’язав Ігор.
888. Подайте вираз у вигляді многочлена:
1) (7х – 1)2 – (2х – 1)(3х -1);
2) (2х – 3)(2х + 3) – (4х – 5)(х + 1);
3) 8х(2х – 5) – (4х – + 3)2;
4) (4х – 7)(4х + 7) (2х – 5)(2х + 5).
889. Знайдіть нулі функції:
1) у – 36 – х2;
2) у =  Х2 – 3х.
Х2 – 3х.
890. Побудуйте графік функції:
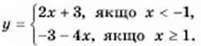
Цікаві задачі для учнів неледачих
891. Відомо, що х + у = 13. При яких натуральних значеннях х і у вираз ху набуває найбільшого значення?