Головна ⇒ 📌ГДЗ з математики ⇒ Лінійні рівняння з однією змінною

Лінійні рівняння з однією змінною

793. Лінійними рівняннями є рівняння: а) 2/9х = 8; в) -2,7y = 0.

794. а) 56х = 64; рівняння має 1 корінь,

Лінійні рівняння з однією змінною

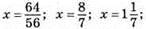
Б) 0х = -2; рівняння не має коренів;

В) 8х = 0; рівняння має 1 корінь, х = 0;

Г) 0у = 0; рівняння має безліч коренів.

795. а) 6х = 42; х = 42 : 6; х = 7;

Б) 4х = -12; х = -12 : 4; х = -3;

В) -3у = 6; у = 6 : (-3); у = -2;

Г) -5z = -45; z = -45 : (-5); z = 9;

Д) 3х = -2; х = -2/3;

Е) 0у = -4; рівняння не має коренів;

Є) Ох = 0; любе число є коренем рівняння;

Ж) -2х = 0; х = 0.

796. а) 36х = -54; х = -54 : 36; x = -1,5.

Відповідь: -1,5.

Б) 0,04z = 1,4; z = 1,4 : 0,04; z = 35.

Відповідь: 35.

В) 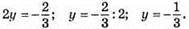Лінійні рівняння з однією змінною

class=""/>

Відповідь: -1/3.

Г) -1,2х = -0,09; х = -0,09 : (-1,2); х = 0,075.

Відповідь: 0,075.

Д) -3,86t = 7,913; t = 7,913 : (-3,86); t = -2,05.

Відповідь: -2,05.

Е) 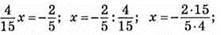Лінійні рівняння з однією змінною х = -1,5.

Відповідь: -1,5.

797. а) 5х – 3 = 17; 5х = 17 + 3; 5х = 20; х = 20 : 5; х = 4.

Відповідь; 4.

Б) 7х + 32 = 12х + 25; 7х – 12х = 25 – 32; -5х = -7; х = -7 : (-5); х = 1,4.

Відповідь: 1,4.

В) 4 – 3у = 6у + 22; 6у + 3у = 4 – 22; 9у = -18; у = -18 : 9; у = -2.

Відповідь: -2.

Г) 4,5z + 1 = 7z + 2,5; 7z – 4,5z = 1 – 2,5; 2,5z = -1,5; z = -1,5 : 2,5; z = -0,6.

Відповідь: -0,6.

Д) -1,2m – 2 = m – 0,9; -1,2m – m = -0,9 + 2; -2,2m = 1,1; m = 1,1 : (-2,2); m = -0,5.

Відповідь: -0,5.

Е) -1,74х + 7,92 = -1,08х; -1,74х + 1,08х = -7,92; -0,66х = -7,92; х = -7,92 : (-0,66); х = 12.

Відповідь:

12.

798. а) 56х = -196; х = -196 : 56; х = -3,5.

Відповідь: -3,5.

Б) 8х = -8 + 12х; 12х – 8х = 8; 4х = 8; х = 8 : 4; х = 2.

Відповідь: 2.

В) 6х + 2 = 20х – 5; 20х – 6х = 5 + 2; 14х = 7; х = 7 : 14; х = 0,5.

Відповідь: 0,5.

Г) 2у – 18 = -3у + 67; 2у + 3у = 67 + 18; 5у = 85; у = 85 : 5; у = 17.

Відповідь: 17.

Д) 1,15 – 3z = 2,5; 3z = 1,15 – 2,5; 3z = -1,35; z = -1,35 : 3; z = -0,45.

Відповідь: -0,45.

Е) 4,5х + 1 = 2 + 4,5х; 4,5х – 4,5х = 2 – 1; 0 • х = 1.

Відповідь: не має розв’язку.

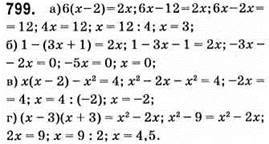
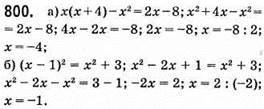
Лінійні рівняння з однією змінною

Лінійні рівняння з однією змінною

Рівень Б

801. а) 2(х – 11) – 5(5 – 2х) = -23; 2х – 22 – 25 + 10x = -23; 12x – 47 = -23; 12x = -23 + 47; 12x = 24; x = 24 : 12; x = 2.

Відповідь: 2.

Б) 8(-3x + 4) + 14(3 + 2х) = 4 + 2х. Поділимо обидві частини рівняння на 2, отримаємо: 4(-3x + 4) – 7(3 + 2х) = 2 + х; -12х + 16 + 21 + 14x = 2 + х; 2х + 37 = 2 + х; 2х – х = 2 – 37; х = -35.

Відповідь: -35.

В) -5(4x + 3) + 3x = -12(x – 3); -20x – 15 + 3х = -12х + 36; -17х – 15 = -12х + 36; 17x – 12x = -15 – 36; 5х = -51; x = -10,2.

Відповідь: -10,2.

Г) 0,5x = 0,1(2x – 5) + 1,7; 0,5x = 0,2x – 0,5 + 1,7; 0,5x – 0,2x = -0,5 + 1,7; 0,3x = 1,2; x = 1,2 : 0,3; x = 4.

Відповідь: 4.

Лінійні рівняння з однією змінною

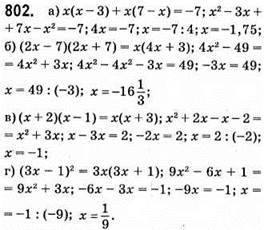
803. а) 5(3x – 6) + 4(3 – 2x) = 5x – 8; 15x – 30 + 12 – 8x = 5x – 8; 7x – 18 = 5x – 8; 7x – 5 = -8 + 18; 2x = 10; x = 10 : 2; x = 5.

Відповідь: 5.

Б) 9(x – 3) – 4(7 – 3x) – 5 = -3x; 9x – 27 – 28 + 12x – 5 = -3x; 21x – 60 = -3x; 21x + 3x = 60; 24x = 60; x = 60 : 24; x = 2,5.

Відповідь: 2,5.

В) -0,3(8 – 4x) = 0,6(x – 3) + 0,9. Поділимо обидві частини рівняння на 0,3, отримаємо: -(8 – 4x) = 2(x – 3) + 3; -8 + 4x = 2x – 6 + 3; -4x – 2x = -3 + 8; 2x = 5; x = 5 : 2; x = 2,5.

Відповідь: 2,5.

Г) 2(-0,9x + 1,4) + 1,4(1,5 + x) = x; -1,8x + 2,8 + 2,1 + 1,4x = x; -0,4x – x = -4,9; -1,4x = -4,9; x = -4,9 : (-1,4); x = 3,5.

Відповідь: 3,5.

Д) (x – 1)(2x + 3) = 2×2 + 2x; 2×2 – 2x + 3x – 3 = 2×2 + 2x; 2×2 + x – 2×2 – 2x = 3; – x = 3; x = -3;

Е) (x + 2)2 = (x – 4)(x + 4); x2 + 4x + 4 = x2 – 16; 4x = -16 – 4; 4x = -20; x = -20 : 4; x = -5.

804. Маємо розв’язати рівняння, щоб знайти x: 2x – 3 = -3 + 7x; 2x = 7x; -5x = 0; x = 0. Тому значення виразів 2x – 3 і -3 + 7x дорівнюють одне одному, якщо x = 0.

805. Розв’яжемо рівняння: 25x – 30 – 5 = 15x + 15; 25x – 35 = 15x + 15; 25x – 15x = 35 + 15; 10x = 50; x = 50 : 10; x= 5. Отже, значення виразу 25x – 10 на 5 менше від значення виразу 15x+ 15, якщо x = 5.

806. Розв’яжемо рівняння 4x + 6 = 6(6x – 15). 4x + 6 = 36x – 90; 36x – 4x = 6 + 90; 32x = 96; x = 96 : 32; x = 3. Отже, значення виразу 4x + 6 у 6 разів більше від значення виразу 6x – 15, якщо x = 3.

807. Розв’яжемо рівняння -2x + 3 = 7; -2x = 7 – 3; -2x = 4; x = 4 : (-2); x = 2. Отже, значення функції дорівнює 7 при x = 2.

808. Розв’яжемо рівняння 4x – 5 = 1 – 2x; 4x + 2x = 1 + 5; 6x = 6; x = 6 : 6; x = 1; у = 4 • 1 – 5 = -1. Отже, (1; -1) – точка перетину графіків даних функцій.

809. а) 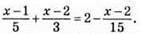Лінійні рівняння з однією змінною Домножимо обидві частини рівняння на 15, отримаємо: 3(x – 1) + 5(x – 2) = 15 • 2 – (x – 2); 3x – 3 + 5x – 10 = 30 – x + 2; 8x – 13 = 32 – x; 8x + x = 32 + 13; 9x = 45; x= 45 : 9; x = 5.

Відповідь: 5.

Лінійні рівняння з однією змінною

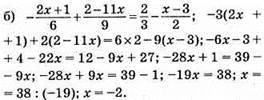
Відповідь: -2.

Лінійні рівняння з однією змінною

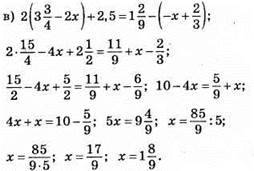
Відповідь: Лінійні рівняння з однією змінною

Лінійні рівняння з однією змінною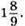

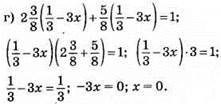
Відповідь: 0.

810. а) 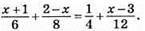Лінійні рівняння з однією змінною Домножимо обидві частини рівняння на 24, отримаємо: 4(х + 1) + 3(2 – х) = 6 • 1 + 2(х – 3); 4х + 4 + 6 – 3х = 6 + 2х – 6; х + 10 = 2х; 2х – х = 10; х = 10.

Відповідь: 10.

Б) 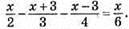Лінійні рівняння з однією змінною Домножимо обидві частини рівняння на 12, отримаємо: 6х – 4(х + 3) + 3(х – 3) = 2х; 6х – 3х – 12 – 3х + 9 = 2х; – х – 3 = 2х; 2х + х = -3; 3х = -2/3; х = -3 : 3; х = -1.

Відповідь: -1.

Лінійні рівняння з однією змінною

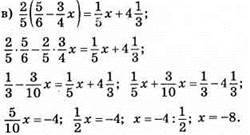
Відповідь: -8.

Лінійні рівняння з однією змінною

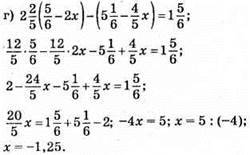
Відповідь: -1,25.

Рівень В

811. а) 200(2(2(х – 1) – 1) – 1) = -600. Поділимо обидві частини рівняння на 200, отримаємо: 2(2(х – 1) – 1) – 1) = -3; 2(2х – 2 – 1) – 1 = -3; 2(2х – 3) = -2; 2х – 3 = -1; 2х = 2; х = 1.

Відповідь: 1.

Лінійні рівняння з однією змінною

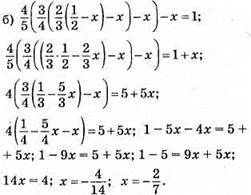
Відповідь: -2/7.

Лінійні рівняння з однією змінною

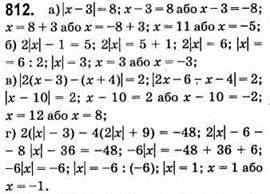
813. а) 3х + |х| = 20. Якщо х – додатне, то 3х + х = 20; 4х = 20; х = 20 : 4; х = 5.

Якщо х – від’ємне, то 3х – х = 20; 2х = 20; х = 10 – не є коренем, бо не є від’ємним.

Відповідь: х = 5.

Б) 5|х| + х = 12. Якщо х – додатне, то 5х + х = 12; 6x = 12; х = 2.

Якщо х – від’ємне, то -5х + х = 12; -4х = 12; х = -3.

Відповідь: х = 2; х = -3.

В) х – |х| = 12. Якщо х – додатне, то х – х = 12; 0х = 12; рівняння коренів не має.

Якщо х – від’ємне, то х – |х| = 12; х + х = 12; 2х = 12; х = 6 – не є коренем, бо не є від’ємним.

Відповідь: коренів немає.

Г) х – |х| = 0. Якщо х – додатне, то x – x = 0; 0х = 0; будь-яке число є коренем.

Якщо х – від’ємне, то х + х = 0; 2х = 0; х = 0 – не є від’ємним.

Відповідь: коренем є любе невід’ємне число.

Вправи для повторення

Лінійні рівняння з однією змінною

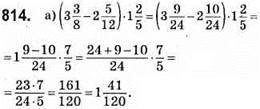
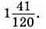
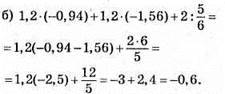
Відповідь: Лінійні рівняння з однією змінною

Лінійні рівняння з однією змінною

Відповідь: -0,6.

815. = 1,5(a + b).

816. S = 0,2(a – b).

817. S = 2(а + b) + 3(а – b) = 2а + 2b + 3а – 3b = 5а – b.

818. Якщо корінь даного рівняння ах = 4389, де а = **1, є натуральним числом, тоді воно повинно закінчуватися цифрою 9, тому х = 19, якщо а = 231.

Відповідь: 19.


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Лінійне рівняння з однією змінною. Розв’язування лінійних рівнянь з однією змінною і рівнянь, що зводяться до них Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ & 23. Лінійне рівняння з однією змінною. Розв’язування лінійних рівнянь з однією змінною і рівнянь, що зводяться до них Ми знаємо, як розв’язувати рівняння 2х = -8; х – 5; 0,01х -17. Кожне із цих рівнянь має вигляд ах = b, де х – змінна, а і b […]...

  2. Лінійне рівняння з однією змінною Урок № 11 Тема. Лінійне рівняння з однією змінною Мета: перевірити рівень засвоєння знань, умінь та навичок, передбачених програмою, в ході вивчення названої теми. Тип уроку: контроль знань. Хід уроку І. Умова тематичної контрольної роботи Варіант 1 Варіант 2 № 1. Чи рівносильні рівняння? Чому? 3х + 4 = 7 та 2(х + 3) – […]...

  3. Лінійні нерівності з однією змінною УРОК № 12 Тема. Лінійні нерівності з однією змінною Мета уроку: домогтися закріплення учнями змісту: означення рівносильних нерівностей та властивостей рівносильних нерівностей; означення лінійної нерівності з однією змінною та схеми Ті розв’язування залежно від різних значень коефіцієнтів. Доповнити знання учнів уявленням про схему дій при розв’язування нерівностей з однією змінною, що містять дроби із числовими […]...

  4. ЛІНІЙНЕ РІВНЯННЯ З ОДНІЄЮ ЗМІННОЮ РОЗДІЛ 5 ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ &20. ЛІНІЙНЕ РІВНЯННЯ З ОДНІЄЮ ЗМІННОЮ Ви вже знаєте, що рівняння можна поділити на види за кількістю змінних. У цьому параграфі розглядатимемо рівняння з однією змінною. Запам’ятайте! Рівняння виду ах + b = 0, де х – змінна, а і b – деякі числа, називається лінійним рівнянням з […]...

  5. Нерівність з однією змінною. Система та сукупність нерівностей з однією змінною УРОК № 9 Тема. Нерівність з однією змінною. Система та сукупність нерівностей з однією змінною Мета уроку: засвоєння учнями змісту понять: нерівність з однією змінною, розв’язок нерівності з однією змінною та що означає розв’язати нерівність з однією змінною; система нерівностей з однією змінною, розв’язок системи нерівностей з однією змінною та що означає розв’язати систему нерівностей […]...

  6. Лінійні рівняння та їх системи 831. 3) 7х – 2 = 10; 1), 2), 4) – не є рівняннями. 832. 1) 2х = 6; х = 3 – корінь рівняння; 4) 27 : х = 9; х = 3 – корінь рівняння. 833. 1) х + 7 = 9; х = 2 – розв’язок; 3) х – 8 = -6; […]...

  7. Рівняння. Нерівності зі змінною Рівняння. Нерівності зі змінною 1 Розбий записи на дві групи. Назви кожну групу. 27 + х = 51 27 + х < 51 40 ∙ р > 160 2 Згадай, що ти знаєш про рівняння; про нерівності зі змінною. Розглянь, як учні розв’язали рівняння та нерівність способом добору. Прокоментуй їхні дії. Із чисел 1, 2, […]...

  8. Лінійні рівняння з одним невідомим Математика – Алгебра Рівняння Лінійні рівняння з одним невідомим Рівняння виду , де a і b – деякі числа, а х – невідоме, називається Лінійним рівнянням з одним невідомим. Числа a і b називають Коефіцієнтами. Кількість коренів лінійного рівняння 1. Якщо , лінійне рівняння має єдиний корінь: . 2. Якщо , , лінійне рівняння коренів […]...

  9. Системи нерівностей з однією змінною Математика – Алгебра Нерівності Системи нерівностей з однією змінною Розв’язком системи нерівностей з однією змінною називають значення змінної, яке є розв’язком кожної нерівності даної системи. Розв’язати систему нерівностей означає знайти всі її розв’язки або показати, що їх немає. Щоб розв’язати систему нерівностей, кожну її нерівність поступово спрощують, замінюючи рівносильною. Розглянемо на простих прикладах, як застосувати […]...

  10. Розділ 5. Лінійні рівняння та їх системи Рівносильні, бо корені однакові. Не рівносильні, бо корені різні. – один корінь; – коренів немає. 5. Нехай у 7-Б класі навчається х учнів, тоді у 7-А класі навчається (х + 3) учнів. Оскільки загальна кількість учнів у 7-А та 7-Б дорівнює 55, складемо та розв’яжемо рівняння: Х + х + 3 = 55; 2х = […]...

  11. Розв’язування лінійних рівнянь з однією змінною Урок № 99 Тема. Розв’язування лінійних рівнянь з однією змінною Мета: закріпити знання учнів про властивості рівносильності рівнянь та способи їх застосування для розв’язування лінійних рівнянь з однією змінною; вдосконалити вміння учнів розв’язувати лінійні рівняння з однією змінною з використанням зазначених вище знань. Тип уроку: засвоєння вмінь та навичок. Хід уроку I. Організаційний момент II. […]...

  12. Нерівності з однією змінною УРОК № 63 Тема. Нерівності з однією змінною Тестові завдання 1. Дано нерівності: 1) -2х2 + х + 6 < 0; 2) 2х2 + х + 7 ? 0; 3) х2 > 0; 4) -3х2 – х – 6 < 0. 2. Яка з даних нерівностей виконується при будь-яких значеннях x? а) усі; б) 2; […]...

  13. Розв’язування нерівностей з однією змінною Математика – Алгебра Нерівності Розв’язування нерівностей з однією змінною Розв’язком нерівності з однією змінною називається значення цієї змінної, яке перетворює її на правильну числову нерівність. Розв’язати нерівність означає знайти всі її розв’язки або довести, що їх немає. Дві нерівності називають Рівносильними, якщо вони мають одні й ті самі розв’язки або не мають розв’язків. Числові проміжки […]...

  14. Рівняння. Нерівності зі змінною Мета: узагальнити й систематизувати навчальний досвід учнів відносно рівнянь і нерівностей зі змінною, способів їх розв’язування. Дидактичні задачі. Вдосконалювати навички позатабличного множення та ділення – усна лічба. Класифікувати записи на рівності та нерівності зі змінною. Актуалізувати поняття рівняння, “розв’язок рівняння”, “розв’язати рівняння”; поняття нерівності зі змінною; розуміння способу добору числа для розв’язування рівнянь та нерівностей. […]...

  15. Розв’язування систем (та сукупностей) лінійних нерівностей з однією змінною УРОК № 14 Тема. Розв’язування систем (та сукупностей) лінійних нерівностей з однією змінною Мета уроку: закріплення учнями знань змісту понять: нерівність з однією змінною, розв’язок нерівності з однією змінною та що означає розв’язати нерівність з однією змінною; система нерівностей з однією змінною, розв’язок системи нерівностей з однією змінною та що означає розв’язати систему нерівностей з […]...

  16. ЛІНІЙНІ РІВНЯННЯ ТА їХ СИСТЕМИ ЯК МАТЕМАТИЧНІ МОДЕЛІ ТЕКСТОВИХ ЗАДАЧ. РОЗВ’ЯЗУВАННЯ ЗАДАЧ ЗА ДОПОМОГОЮ ЛІНІЙНИХ РІВНЯНЬ Цілі: – навчальна: сформувати уявлення про прикладні задачі та математичні моделі задач; сформувати вміння складати та розв’язувати рівняння, що є математичними моделями прикладних текстових задач; домогтися засвоєння схеми розв’язання задач за допомогою лінійних рівнянь; – розвивальна: розвивати увагу, логічне мислення, пам’ять; формувати вміння вибирати і використовувати необхідну інформацію для розв’язування задач; – виховна: виховувати інтерес […]...

  17. Поняття рівняння. Розв’язування рівнянь 770. а) 5х = 3х + 4. Х = 2 – корінь рівняння, бo 5 • 2 = 3 • 2 + 4 – правильна рівність. Б) 2х + 8 = 7х. Х = 2 – не є коренем рівняння, 2 • 2 + 8 = 7 • 2 – неправильна рівність. В) 10 – […]...

  18. Графік лінійного рівняння із двома змінними 894. (0; 1); (-1; 0); (2; 3). 895. 2х – у = 1. А) A(1; 1) – належить графіку даного рівняння, бо 2 • 1 – 1 = 1 – правильна рівність; Б) В(2; 1) – не належить графіку даного рівняння, бо 2 • 2 – 1 = 1 – неправильна рівність; В) С(0; 1) […]...

  19. Рівняння із вдома змінними 870. Рівняння із двома змінними: б) x + 2у = 7; г) х – у = 1; д) 12x + 10у = 0; е) 0x – 2у = 3; ж) 3x + 0у = 0; ж) 0x + 0у = 0; з) 0x + 0y = 1. 871. 2х – у = 3. А) x […]...

  20. РІВНЯННЯ СТАНУ ІДЕАЛЬНОГО ГАЗУ (РІВНЯННЯ КЛАПЕЙРОНА – МЕНДЕЛЄЄВА) – ВЛАСТИВОСТІ ГАЗІВ (ГАЗОВІ ЗАКОНИ) Фізика підготовка до ЗНО комплексне видання МОЛЕКУЛЯРНА ФІЗИКА І ТЕРМОДИНАМІКА 2. ВЛАСТИВОСТІ ГАЗІВ (ГАЗОВІ ЗАКОНИ) – Не зберігають ні форми, ні об’єму. – Характер молекулярного руху: безладний (хаотичний) рух. 2.1. РІВНЯННЯ СТАНУ ІДЕАЛЬНОГО ГАЗУ (РІВНЯННЯ КЛАПЕЙРОНА – МЕНДЕЛЄЄВА) Рівняння стану ідеального газу зв’язує макроскопічні параметри р, V, Т, які характеризують стан даної маси тіла. Рівняння […]...

  21. ІДЕАЛЬНИЙ ГАЗ. ОСНОВНЕ РІВНЯННЯ МОЛЕКУЛЯРНО-КІНЕТИЧНОЇ ТЕОРІЇ ІДЕАЛЬНОГО ГАЗУ (РІВНЯННЯ КЛАУЗІУСА) Фізика підготовка до ЗНО комплексне видання МОЛЕКУЛЯРНА ФІЗИКА І ТЕРМОДИНАМІКА 1. ОСНОВИ МОЛЕКУЛЯРНО-КІНЕТИЧНОЇ ТЕОРІЇ 1.5. ІДЕАЛЬНИЙ ГАЗ. ОСНОВНЕ РІВНЯННЯ МОЛЕКУЛЯРНО-КІНЕТИЧНОЇ ТЕОРІЇ ІДЕАЛЬНОГО ГАЗУ (РІВНЯННЯ КЛАУЗІУСА) Ідеальний газ – де газ, у якому середня відстань між молекулами набагато більша від розмірів молекул, і тому в ньому потенціальною енергією молекул нехтують (рис. 3). Рис. З Середня квадратична […]...

  22. Означення квадратного рівняння. Неповні квадратні рівняння та їх розв’язування Урок № 48 Тема. Означення квадратного рівняння. Неповні квадратні рівняння та їх розв’язування Мета: закріпити знання учнів щодо означення квадратного рівняння, коефіцієнтів квадратного рівняння та його видів; домогтися засвоєння учнями способів розв’язання неповних квадратних рівнянь; сформувати вміння застосовувати вивчений матеріал для розв’язування неповних квадратних рівнянь. Тип уроку: засвоєння знань та вмінь. Наочність та обладнання: опорний […]...

  23. РІВНЯННЯ. РОЗВ’ЯЗОК (корінь) РІВНЯННЯ. РОЗВ’ЯЗУВАННЯ ЗАДАЧІ ЗА ПЛАНОМ Мета: ознайомити учнів з поняттям “рівняння”, алгоритмом розв’язання рівняння; формувати вміння розв’язувати задачі за поданим планом; вдосконалювати обчислювальні навички; виховувати інтерес до математики. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ (додаток) 1. Перевірка домашнього завдання 2. “Веселі задачі” – Веселунчик, пес вухатий, Дуже любить рахувати: 28 каченят, На 9 більше гусенят. Скільки разом […]...

  24. Тематична контрольна робота з теми “Квадратні рівняння. Формула коренів квадратного рівняння. Теорема Вієта” Урок № 55 Тема. Тематична контрольна робота з теми “Квадратні рівняння. Формула коренів квадратного рівняння. Теорема Вієта” Мета: перевірити рівень засвоєння учнями змісту основних понять теми “Квадратні рівняння” та рівень умінь, сформованих у ході вивчення теми. Тип уроку: контроль знань та вмінь. Хід уроку I. Організаційний етап II. Перевірка домашнього завдання Зібрати зошити із виконаною […]...

  25. Квадратні рівняння Тестові завдання Тестове завдання № 4 . Квадратні рівняння 1. Яке з рівнянь є квадратним? А Б В Г 7х – 3 = 0 (х – 1)2 = х2 – 4х 5х2 = 4х2 2. Знайдіть коефіцієнти a, b і с квадратного рівняння 3 – х2 – 6х = 0. А Б В Г 3; […]...

  26. Показникові рівняння УРОК 45 Тема. Показникові рівняння Мета уроку. Формування умінь учнів розв’язувати найпростіші показникові рівняння. І. Перевірка домашнього завдання 1. Учитель відповідає на питання учнів, що виникли в процесі виконання домашніх завдань. 2. Самостійна робота Початковий рівень (2 бали) 1) Які з поданих функцій у = 5х; ; ; є Зростаючими? Спадними? Середній рівень (3 бали) […]...

  27. Рівняння з двома змінними 909. Рівняннями з двома змінними є рівняння; 1), 3), 5), 6), 8), 9). 910. 1) 4x + 3y = 1; 4 • (-2) + 3 • 3 = 1 – правильна рівність, тому (-2; 3) – розв’язок даного рівняння. 2) x2 + 5 = у2; (-2)2 + 5 = 32 – правильна рівність, тому (-2; […]...

  28. Логарифмічні рівняння УРОК 57 Тема. Логарифмічні рівняння Мета уроку. Формування умінь учнів розв’язувати логарифмічні рівняння. І. Перевірка домашнього завдання 1. Фронтальна бесіда за № 15-25 із “Запитання і завдання для повторення” розділу V та відповіді на запитання, які виник­ли в учнів у процесі виконання домашніх завдань. 2. Виконання вправ, аналогічних домашнім: № 47 (1; 3), 51. II. […]...

  29. Найпростіші ірраціональні рівняння УРОК 37 Тема. Найпростіші ірраціональні рівняння Мета уроку. Познайомити учнів з методами розв’язування ірраціональних рівнянь. Формування умінь розв’язувати ірраціональні рівняння. І. Перевірка домашнього завдання 1. Фронтальна бесіда за запитаннями № 38-46 із “Запитання і завдання для повторення до розділу III”. 2. Розв’язування вправ, аналогічних до домашніх. А) Обчислити . Відповідь: 3. Б) Обчислити . Відповідь: […]...

  30. Системи рівнянь – РІВНЯННЯ Формули й таблиці МАТЕМАТИКА РІВНЯННЯ Лінійне рівняння з однією змінною – рівняння, що зводиться до канонічного вигляду ах + b = 0, де х – змінна, а й b – константи. Корінь рівняння ах + b = 0 визначається формулою: х = – b/а – якщо а ≠ 0, множина розв’язків L = {-b/a}. – […]...

  31. Розв’язування найпростіших тригонометричних рівнянь. Рівняння tg t = a УРОК 22 Тема. Розв’язування найпростіших тригонометричних рівнянь. Рівняння tg T = a. Мета уроку: зсвоєння учнями виведення і застосування фор­мули для знаходження коренів рівняння tg t = a (ctg t = а). Обладнання: Таблиця “Рівняння tg t = а і ctg t = a”. І. Перевірка домашнього завдання 1. Перевірити наявність домашніх завдань в зошитах […]...

  32. Рівняння та його корені. Рівносильні рівняння Урок № 4 Тема. Рівняння та його корені. Рівносильні рівняння Мета: пояснити, розширити та узагальнити відомості про властивості рівносильних рівнянь та способах їх застосування до розв’язування найпростіших рівнянь з однією змінною. Тип уроку: систематизація, поглиблення та узагальнення знань, умінь, навичок. Хід уроку I. Організаційний момент II. Перевірка домашнього завдання № 1, 3 перевіряємо під час […]...

  33. Підсумковий урок з теми “Квадратні рівняння. Формула коренів квадратного рівняння. Теорема Вієта” Урок № 54 Тема. Підсумковий урок з теми “Квадратні рівняння. Формула коренів квадратного рівняння. Теорема Вієта” Мета: повторити, систематизувати та узагальнити знання і вміння учнів щодо виділення квадратних рівнянь серед інших рівнянь з однією змінною, класифікації квадратних рівнянь, а також застосування різних (передбачених програмою з математики) способів розв’язання квадратних рівнянь різного виду. Тип уроку: систематизація […]...

  34. Рівняння. Основна властивість рівняння Урок № 96 Тема. Рівняння. Основна властивість рівняння Мета: продовжити роботу з вироблення вмінь правильно переносити доданки з однієї частини рівняння в іншу; сформувати уявлення про другу основну властивість рівнянь та розпочати роботу з вироблення вмінь використовувати множення або ділення обох частин рівняння на одне й те саме число, відмінне від 0, для розв’язування рівнянь. […]...

  35. Формула коренів квадратного рівняння Математика – Алгебра Квадратні корені Формула коренів квадратного рівняння Корені квадратного рівняння знаходять за формулою . Вираз називається Дискримінантом і позначається буквою D. Кількість коренів 1. Якщо , рівняння не має коренів. 2. Якщо , рівняння має один корінь: . 3. Якщо , рівняння має два корені: . Для квадратних рівнянь із парним другим коефіцієнтом […]...

  36. Розв’язування найпростіших тригонометричних рівнянь. Рівняння sin t = a УРОК 21 Тема. Розв’язування найпростіших тригонометричних рівнянь. Рівняння sin t = а Мета уроку: засвоєння учнями виведення і застосування формули для коренів рівняння sin t = а. Обладнання: Таблиця “Рівняння sin t = а”. І. Перевірка домашнього завдання 1. Відповіді на питання, що виникли при виконанні домашніх завдань. 2. Самостійна робота. Варіант 1 Розв’яжіть рівняння: […]...

  37. Рівняння прямої УРОК № 28 Тема. Рівняння прямої Мета уроку: виведення рівняння прямої. Формування вмінь учнів використовувати рівняння прямої до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати і вектори на площині” [13]. Вимоги до рівня підготовки учнів: записують і пояснюють рівняння прямої. Розпізнають рівняння прямої. Хід уроку I. Перевірка домашнього завдання Перевірити наявність […]...

  38. Розв’язування найпростіших тригонометричних рівнянь. Рівняння cos t = a УРОК 20 Тема. Розв’язування найпростіших тригонометричних рівнянь. Рівняння cos T = a Мета уроку: засвоєння учнями виведення і застосування фор­мули для знаходження коренів рівняння cos t = a. Обладнання: Таблиця “Рівняння cos t = a”. І. Перевірка домашнього завдання Математичний диктант Обчисліть: 1) arcsin ; 2) arcos ; 3) arctg ; 4) arcsin; 5) arccos; […]...

  39. Метод координат. Рівняння сфери, площини, прямої Завдання 2 1. 1) Рівняння сфери, усі точки якої рівновіддалені від початку координат на 1 од. має вигляд х2 + у2 + z2= 1. 2) Оскільки центр сфери – початок координат і вона перетинає ось Оz у точці (0; 0; 1), то вона має радіус 1, а значить, її рівняння; х2 + у2 + z2 […]...

  40. Розв’язування квадратного рівняння – Виділення повного квадрата Математика – Алгебра Квадратні корені Виділення повного квадрата Розв’язування квадратного рівняння Способом виділення квадратного дво­члена розглянемо на прикладі. . Розв’язання Поділимо всі коефіцієнти рівняння на перший коефіцієнт: й отримаємо таким чином зведене квадратне рівняння: ; . Для того щоб отримати повний квад­рат, треба додати і відняти від лівої частини рівняння : , , або , […]...

Ви зараз читаєте: Лінійні рівняння з однією змінною
«
»