Головна ⇒ 📌ГДЗ з математики ⇒ Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника

Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника

Розділ 3. Трикутники. Ознаки рівності трикутників

§ 15. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника

351. 1) AT – висота трикутника ABC.

2) AN – медіана трикутника ABC.

3) АР – бісектриса трикутника? AВС.

352. Оскільки AK – висота, то ∠BKA = ∠CKA = 90°.

353. Оскільки АК – бісектриса, то ∠BAK = ∠CAK = 35°. Отже, ∠BAC = ∠BAK + ∠CAK = 35° + 35° = 70°.

354. Оскільки АК – медіана, то Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника

355.

Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника

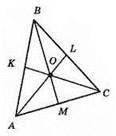
AL, BN, СК – медіани? ABC.

356. PL, CP, AM – бісектриси?

АВС.

Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника

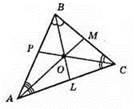
357.

Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника

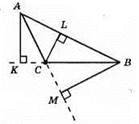
AK, CL, BM – висоти? ABC.

358.

Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника

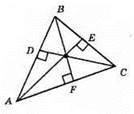
AE, BF, CD – висоти? ABC.

359. Оскільки висота рівнобедреного трикутника, проведена до основи, є медіаною і бісектрисою, то: ∠CAK = ∠BAK, ∠ACK = ∠ABK, ∠AKC = ∠AKB, AC = AB, CK = KB.

360. Оскільки бісектриса рівнобедреного трикутника, проведена до основи, є медіаною і висотою, то: ∠EDP = ∠EFP, ∠DEP = ∠EFP, ∠EPD = ∠EPF, ED = EF, DP = PF.

362. Якщо у трикутника два кути рівні, то він – рівнобедрений. ∠B = ∠C, отже, ВС – основа трикутника. Бісектриса, проведена до основи, є медіаною і висотою. Значить,

бісектриса проведена до сторони ВС.

364.

Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника

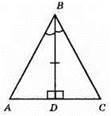
Нехай в? ABC BD – бісектриса і висота. ∠ABD = ∠CBD, ∠BDA = ∠BDC, BD – спільна сторона? ABD і? CBD. Отже, ?ABD = ?CBD за стороною і прилеглими кутами. Оскільки у рівних трикутників відповідні сторони рівні, то AB = СВ. Отже, ?ABC – рівнобедрений.

365.

Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника

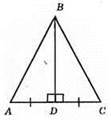
Нехай в? ABC BD – медіана і висота. ∠BDA = ∠BDC = 90°, AD = DC, BD – спільна сторона? ABD і? CBD. Отже, ?ABD = ?CBD за двома сторонами і кутом між ними. Оскільки у рівних трикутників відповідні сторони рівні, то AB = СВ. Отже, ?АВС – рівнобедрений.

366.

Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника

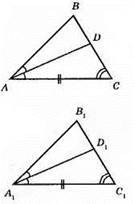
?ABC = ?A1B1C1, отже, A1C1 = АС, ∠B1C1A1 = ∠BCA (як відповідні сторони і кути рівних трикутників). AB – бісектриса? ABC, ∠BAD = ∠DAC. A1D1 – бісектриса? A1B1C1, ∠B1A1D1 = ∠D1A1C1.Отже, ∠DAC = ∠D1A1C1. ?ADC = ?А1D1С1 – за стороною і прилеглими кутами.

367.

Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника

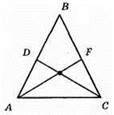
Нехай в? АВС АВ = ВС, BF = FC = 1/2BC, BD = DA = 1/2AВ, отже, AD = FC. ?ADC = ?CFА (оскільки АС – спільна, ∠DAC = ∠FCA – як кути при основі рівнобедреного трикутника, AD = FC – як половини рівних сторін AB і ВС). З рівності трикутників маємо: DC = FA.

368.

Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника

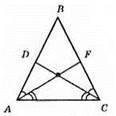
Нехай в? ABC AB = ВС, ∠BAC = ∠BCA, AF і CD – бісектриси, тобто ∠FAC = ∠FAB = 1/2∠BAC, ∠DCA = ∠DCB = 1/2BCA, отже, ∠FAC = ∠DCA, ?ADC = ?CFA (оскільки АС – спільна, ∠FAC = ∠DCA,∠DAC = ∠FCA). З рівності трикутників маємо: AB = CD.

369.

Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника

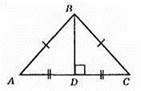
Нехай в? ABC AB = ВС, BD ⊥ АС, BD = 10 CM, P? ABD = 40 CM.

P? ABD = AB + AD + BD, AB + AD = P? ABD – BD = 40 – 10 = 30 (см). AB = BC – за умовою, AD = DC – оскільки BD є медіаною. AB +AD = ВС + DC, тоді P? ABC = AB + AD + ВС + DC = 30 + 30 = 60 (см).

Відповідь: 60 см.

370.

Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника

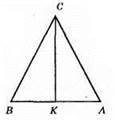
Нехай в? ABC СВ = СА, ВК = КА, P? ABC = 16 см, P? ACK = 12 см.

P? ACK = СА + АK + KС, Р? ABC = CA + AB + BC = CA + AK + KB + BC = 2(CA + KA) = 16 (см). CA + АК = 8 см, KС = Р? ACK – (СА + АK) = 12 – 8 = 4 (см).

Відповідь: 4 см.

371.

Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника

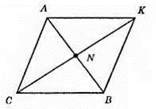
Нехай в? ABC CN – медіана і бісектриса. Продовжимо медіану CN так, щоб NK = CN. Проведемо відрізки КА і КВ. Розглянемо? CNB і? KNA. CN = KN (за побудовою), NB = NA (за умовою). ∠ANK= ∠BNK (як вертикальні), отже, ?CNB = ?KNA за двома сторонами і кутом між ними.

У рівних трикутників рівні відповідні кути і сторони, тож ∠NCB = ∠NKA, СВ = КА. Аналогічно з рівності трикутників CAN і KBN отримаємо ∠CAN = ∠BKN, АС = ВК.

Розглянемо? CAN і? КВС. Вони рівнобедрені. АК = СА, СВ = ВК. Отже, отримали АС = СВ = АК = КВ. У? ABC дві сторони рівні, він рівнобедрений.

372.

Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника

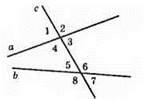
Нехай задані прямі а і b і січна с. Якби а була б паралельна b, TO ∠1 = ∠3 = ∠5 = ∠7, a ∠2 = ∠4 = ∠6 = ∠8 і ∠3 + ∠6 = 180°. Нехай ∠3 = 30°, ∠6 = 140°. ∠3 + ∠6 = 170° ≠ 180°. Отже, сума внутрішніх односторонніх кутів не дорівнює 180°.

Кути ∠6 і ∠7 теж не можуть дорівнювати відповідно 140° і 30°, бо вони суміжні.

373.

Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника

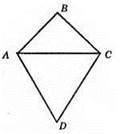
Нехай? ABC – рівносторонній, Р? ABC = 12 см. ?ACD – рівнобедрений. AD = CD, P? ACD = 18 см. AB = BC = АС (як сторони рівностороннього трикутника).

AC = P? ABC : 3 = 12 : 3 = 4 (см).

P? ACD = АС + AD + CD, AD + CD = P? ACD – AC = 18 – 4 = 14 (см). Отже, AD = CD = 7 см.

Відповідь: 7 см.

374.

Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника

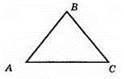
Нехай? ABC – рівнобедрений, AB = BC, Р? ABC = 69 см. Позначимо довжину AB = х см, тоді АС = 0,3x см. Складемо рівняння: x + x + 0,3x = 69; 2,3x = 69; x = 30. Отже, AB = BC = 30 см, АС = 30 x 0,3 = 9 (см).

Відповідь: ЗО см, 30 см, 9 см.

375. 125 л = 125 дм3. Олесь придбав акваріум розмірами 15 дм х 5 дм х 5 дм. Якщо Олесь наповнив акваріум, не доливши до краю 6 см, то він залив води 5 x 5 x 4,4 = 110 (дм3) = 110 л.

Відповідь: 110 л.


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Рівні трикутники. Висота, медіана, бісектриса трикутника § 2. Трикутники 6. Рівні трикутники. Висота, медіана, бісектриса трикутника Практичні завдання 132. 133. ВН – спільна висота трикутників ABD, ABC, BDC. ВН лежить поза трикутником BCD. 134. 135. 136. Вправи 137. 1) ME; 2) ∠E; 3) MK i KE; 4) ∠K i ∠E. 138. 1) ∠E; 2) ∠C i ∠E;3) CF; 4) CF і […]...

  2. Медіана, бісектриса і висота трикутника Урок № 24 Тема. Медіана, бісектриса і висота трикутника Мета: домогтися засвоєння учнями: – змісту понять “медіана трикутника”; “бісектриса трикутника”; “висота трикутника”; – уявлення про положення висот у різних видах трикутника. Сформувати вміння: – зображати медіани, висоти та бісектриси трикутника; – розрізняти ці відрізки, виходячи з умови задачі. Тип уроку: застосування знань, умінь та навичок. […]...

  3. Висота, бісектриса, медіана трикутника Геометрія Основні властивості найпростіших геометричних фігур Висота, бісектриса, медіана трикутника Висотою Трикутника, опущеною з да­ної вершини, називається перпендикуляр, проведений із цієї вершини до прямої, що містить протилежну сторону трикутника. У кожному трикутнику можна провести три висоти. Висоти трикутника (або прямі, що їх містять) перетинаються в одній точці. На рисунках зображено, як перетинаються висоти в гострокутному […]...

  4. Властивість медіани, бісектриси й висоти рівнобедреного трикутника Урок № 25 Тема. Властивість медіани, бісектриси й висоти рівнобедреного трикутника Мета: домогтися свідомого сприйняття учнями змісту теореми про властивість медіани, бісектриси й висоти рівнобедреного трикутника та наслідків з неї; сформувати вміння відтворювати названі властивості та застосовувати їх під час розв’язування задач. Тип уроку: засвоєння знань, умінь та навичок. Наочність і обладнання: набір демонстраційного креслярського […]...

  5. Ознаки рівнобедреного трикутника § 2. Трикутники 9. Ознаки рівнобедреного трикутника 232. ?ABC – рівнобедрений, тому ВК є бісектрисою кута ABC, отже, ∠ABC = 2 х ∠ABK = 2 x 25° = 50°. Відповідь: 50°. 233. BK є висотою та медіаною, тому? ABC – рівнобедрений, AB = ВС, отже, ∠C = ∠A =17°. Відповідь: 17°. 234. AС = ВС, […]...

  6. Властивості й ознака рівнобедреного трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 12. Властивості й ознака рівнобедреного трикутника 476. На мал. 72: ML і МК – бічні сторони, KL – основа, ∠K = ∠L. 477. KD = DF, КЕ = EF, ∠K = ∠F, ∠KDE = ∠FDE, ∠DEK = ∠DEF = 90°. 478. Щоб провести бісектрису, медіану і […]...

  7. Застосування подібності: властивість бісектриси трикутника Урок № 37 Тема. Застосування подібності: властивість бісектриси трикутника Мета: домогтися засвоєння учнями змісту теореми, що виражає властивість бісектриси трикутника та її доведення. Формувати вміння: – відтворювати зміст вивченої теореми; – за готовими рисунками із зображенням трикутника та його бісектриси знаходити пропорційні відрізки; – виконувати записи відповідно до формулювання теореми та умови задачі; – застосовувати […]...

  8. Описане та вписане коло трикутника § 3. Паралельні прямі. Сума кутів трикутника § 20. Описане та вписане коло трикутника 540. 1) Різносторонній гострокутний трикутник. 2) Прямокутний трикутник. 3) Тупокутний трикутник. 541. 1) Рівнобедрений гострокутний трикутник. 2) Рівнобедрений тупокутний трикутник. 542. 543. 544. Вправи 545. Медіана BD рівнобедреного трикутника ABC є в той же час і серединним перпендикуляром до сторони АС […]...

  9. Кут. Вимірювання кутів. Бісектриса кута Розділ 1. Елементарні геометричні фігури та їхні властивості § 3. Кут. Вимірювання кутів. Бісектриса кута 33. 1) М – вершина кута, МА і МК – сторони кута АМК; 2) L – вершина кута, LP і LF – сторони кута PLF; 3) N – вершина кута, NB i NC – сторони кута BNC. 34. 1) O […]...

  10. Зовнішній кут трикутника та його властивості Розділ 3. Трикутники. Ознаки рівності трикутників § 18. Зовнішній кут трикутника та його властивості 438. ∠BAK – зовнішній кут при вершині А. 439. ∠LDP – зовнішній кут при вершині D. 441. ∠A + ∠B = 70° – за властивістю зовнішнього кута трикутника. 442. Зовнішній кут трикутника при вершині С дорівнює 74° згідно з властивістю зовнішнього […]...

  11. Сума кутів трикутника. Нерівність трикутника § 3. Паралельні прямі. Сума кутів трикутника § 15. Сума кутів трикутника. Нерівність трикутника Вправи 357. Нехай х° – третій кут трикутника, тоді 35 + 96 + х = 180, звідси х + 131 = 180; х = 180 – 131; х = 49. Отже, третій кут дорівнює 49°. Відповідь: 49°. 358. Нехай х° – […]...

  12. Властивості кутів трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 10. Властивості кутів трикутника 344. ∠E = 60°, ∠F = 40°, ∠D = 80°. ∠E + ∠F + ∠D = 60° + 40° + 80° = 180°. 345. На мал. 208 неправильно сказано градусну міру кутів? АВС, оскільки? ABC – прямокутний, a ∠B + ∠C = […]...

  13. Властивості прямокутного трикутника § 3. Паралельні прямі. Сума кутів трикутника § 17. Властивості прямокутного трикутника 457. Найбільший катет трикутника дорівнює 24 см. 458. ?DEF – прямокутний, ∠F = 90°, ∠D = 30°, DE = 18 см. Відповідь: 9 см. 459. ?KCM – прямокутний, ∠M = 90°, ∠C = 60°, MC = 7 см. ∠MKC = 90° – 60° […]...

  14. Перша та друга ознаки рівності трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 13. Перша та друга ознаки рівності трикутників 301. На рис. 227 трикутники рівні за першою ознакою (за двома сторонами і кутом між ними). На рис. 228 трикутники рівні за другою ознакою (за стороною і прилеглими двома кутами). 302. У? ABC і? CDA спільний елемент – сторона AВ. У? […]...

  15. Ознаки рівнобедреного трикутника Геометрія Основні властивості найпростіших геометричних фігур Ознаки рівнобедреного трикутника Теорема 1. Якщо в трикутнику два кути рівні, то він рівнобедрений. Теорема 2. Трикутник рівнобедрений, ­якщо: – одна з його висот є медіаною; – одна з його медіан є бісектрисою; – одна з його висот є бісектрисою. Теорема 3. Трикутник рівнобедрений, ­якщо: – дві його висоти […]...

  16. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 19. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників 466. 1) PF – гіпотенуза, PL і LF – катети. 2) PF довша за PL, PF довша за LF, оскільки PF – гіпотенуза. 467. На рис. 321 трикутники рівні за двома катетами. Оскільки АС = ML, СВ = LP, […]...

  17. Рівнобедрений трикутник і його властивості § 2. Трикутники 8. Рівнобедрений трикутник і його властивості Практичні завдання 196. 197. 198. Вправи 199. 1) Р = 13 + 2 х 8 = 29(см). Відповідь: 29 см. 2) Нехай х см – бічна сторона, тоді 15 + 2х = 39, тоді 2х = 39 – 15; 2х = 24; х = 24 : […]...

  18. Трикутник і його елементи Розділ 1. Найпростіші геометричні фігури та їх властивості § 9. Трикутник і його елементи 292. На мал. 194 зображені трикутники ABD, ABC, ОВС. Проти кута C в трикутнику АВС лежить сторона АB, в трикутнику DBC – сторона BD. Прилеглими до кута С в трикутнику ABC є сторони АС і ВС, в трикутнику DBC – сторони […]...

  19. Рівність геометричних фігур Розділ 1. Найпростіші геометричні фігури та їх властивості § 11. Рівність геометричних фігур 397. Щоб сумістити фігури F1 i F, можна скопіювати фігуру F1 на кальку, потім перевернути кальку і покласти на фігуру F. 398. Відрізки OP і MN сумістити не можна, бо вони мають різну довжину. 399. Кути ABC і MON сумістити не можна, […]...

  20. Площа трикутника Геометрія Площі фігур Площа трикутника , де h – висота, a – сторона, до якої проведена ця висота. Оскільки , то . Висоти трикутника обернено пропорційні сторонам, на які вони опущені. Зверніть увагу: більшій стороні трикутника відповідає менша висота, і навпаки. , , де P – периметр трикутника, r – радіус вписаного кола. , , […]...

  21. СУМА КУТІВ ТРИКУТНИКА РОЗДІЛ 3 ТРИКУТНИКИ & 10. СУМА КУТІВ ТРИКУТНИКА Теорема 8 Сума кутів трикутника дорівняй: 180°. Доведення. Нехай ABC – довільний трикутник (мал. 130). Через йот вершину С проведемо пряму КР, паралельну стороні АВ. Утворені кути АСК і ВСР позначимо цифрами 1 і 2. Тоді ∠A = ∠1, ∠B = ∠2, як внутрішні різносторонні кути при […]...

  22. Бісектриса Геометрія Основні властивості найпростіших геометричних фігур Бісектриса Бісектрисою кута називається промінь, який виходить із вершини кута, проходить між його сторонами й ділить кут пополам. На рисунку BD – бісектриса . Властивості бісектриси Теорема 1. Бісектриса кута утворює з його сторонами кути, не більші за . Теорема 2. Бісектриси вертикальних кутів лежать на одній прямій (тобто […]...

  23. Властивість точки, рівновіддаленої від сторін многокутника Урок 36 Тема. Властивість точки, рівновіддаленої від сторін многокутника Мета уроку: формування вмінь учнів застосовувати властивість ортогональної проекції точки, рівновіддаленої від сторін многокутника, до розв’язування задач. Обладнання: стереометричний набір, схема “Коло, вписане в многокутник” Хід уроку 1. Перевірити правильність виконання вправ № 42, 48, 53 за записами, зробленими на дошці до початку уроку. Нехай ABCD […]...

  24. Ознаки паралельності прямих. Сума кутів трикутника Урок № 40 Тема. Ознаки паралельності прямих. Сума кутів трикутника Мета: перевірити рівень засвоєння знань та вмінь, передбачених програмою, із зазначених тем. Тип уроку: контроль та корекція знань. ХІД УРОКУ I. Організаційний момент II. Перевірка домашнього завдання Зібрати зошити з виконаною домашньою контрольною роботою. Роботу оцінити та врахувати в тематичному балі. III. Умова контрольної роботи […]...

  25. НЕРІВНОСТІ ТРИКУТНИКА РОЗДІЛ 3 ТРИКУТНИКИ & 15. НЕРІВНОСТІ ТРИКУТНИКА Ви вже знаєте, що кожна сторона трикутника менша від суми двох інших його сторін. Щоб довести це твердження як теорему, спочатку розглянемо іншу теорему. Теорема 19 У кожному трикутнику проти більшої сторони лежить більший кут, а проти більшого кута – більша сторона. Доведення. 1) Нехай у трикутнику ABC […]...

  26. Дотична до кола, її властивості Розділ 4. Коло і круг. Геометричні побудови § 22. Дотична до кола, її властивості 607. Проведемо радіус ОР, а потім за допомогою косинця побудуємо пряму m, перпендикулярну до радіуса. За теоремою 2 пряма m є дотичною до кола. 608. Проведемо радіус ОМ, а потім за допомогою косинця побудуємо пряму n, перпендикулярну до радіуса. За теоремою […]...

  27. Взаємне розміщення двох кіл Розділ 4. Коло і круг. Геометричні побудови § 25. Взаємне розміщення двох кіл 656. На рис. 404 кола перетинаються. На рис. 405 кола дотикаються. На рис. 406 кола не мають спільних точок. 657. 1) Кола мають внутрішній дотик. 2) Кола перетинаються. 3) Кола концентричні. 658. 1) Кола мають зовнішній дотик. 2) Кола не перетинаються. 659. […]...

  28. Ознаки рівності прямокутних трикутників Розділ 1. Найпростіші геометричні фігури та їх властивості § 14. Ознаки рівності прямокутних трикутників 549. Ні, трикутники не рівні. 550. Мал. 319. ?САВ = ?HDQ (за катетом і гострим кутом: CA = HD, ∠C = ∠H). Мал. 320. ?ABC = ?CDA (за гіпотенузою АС і гострим кутом: ∠BAC = ∠DAC). Мал. 321. ?АОВ = ?DCО […]...

  29. Вправи 275-324 275. Кут В. а) ВА = ВС, ?АВС – рівнобедрений, у нього дві сторони рівні; Б) ∠A = ∠C. 276. ∠A = 60°; AD – бісектриса кута А. BC ⊥ AD; AB = AC; ∠B = ∠C. 277. AB = ВС; АС – основа. Нехай АВ = ВС = х м, тоді АС = (х […]...

  30. Знаходження площі трикутника за двома сторонами і кутом між ними УРОК № 12 Тема. Знаходження площі трикутника за двома сторонами і кутом між ними Мета уроку: виведення формули для знаходження площі трикутника за двома сторонами і кутом між ними. Формування вмінь застосовувати виведену формулу до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Співвідношення між сторонами і кутами трикутника”[13]. Вимоги до рівня підготовки учнів: […]...

  31. Вправи 225-273 225. L ⊥ AB; X – точка прямої l; О – середина AB. ?АОХ = ?BOX (за першою ознакою рівності трикутників). 1) АО = OB; 2) ∠3 = ∠4 = 90°; 3) ОХ – спільна сторона. З цього випливає АХ = ВХ, отже, точка X рівновіддалена від кінців відрізка А і В. 226. Три прямі […]...

  32. Знаходження площі трикутника за радіусом вписаного та описаного кіл УРОК № 14 Тема. Знаходження площі трикутника за радіусом вписаного та описаного кіл Мета уроку: виведення формул для знаходження площі трикутника за радіусом вписаного та описаного кіл. Формування вмінь учнів застосовувати виведені формули до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Площі трикутників і чотирикутників” [13], посібник [14]. Вимоги до рівня підготовки учнів: […]...

  33. Нерівність трикутника Урок № 38 Тема. Нерівність трикутника Мета: домогтися засвоєння змісту теореми, що виражає нерівність трикутника та схему її доведення та наслідку з теореми; виробляти вміння відтворювати формулювання доведених на уроці тверджень та застосувати для розв’язування задач. Тип уроку: засвоєння знань, умінь та навичок. Наочність і обладнання: набір демонстраційного креслярського приладдя; таблиця “Нерівність трикутників та наслідки […]...

  34. Ознаки рівності трикутників Геометрія Основні властивості найпростіших геометричних фігур Ознаки рівності трикутників Теорема 1 (перша ознака рівності трикутників – за двома сторонами й кутом між ­ними). Якщо дві сторони й кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними другого трикутника, то такі трикутники рівні. Теорема 2 (друга ознака рівності трикутників – за стороною […]...

  35. Вправи 475-524 475. ?ABC – прямокутний; ∠A = 30°; АС = 18 см; ВК – бісектриса, проведена до катета АС; ∠CBK = ∠ABK = ∠CBA : 2 = 60° : 2 = 30°; ∠CBA = 90° – ∠CAB = 90° – 30° = 60°; СК = х, тоді AK = 18 – х. ?АВК – прямокутний; ∠A […]...

  36. Кути трикутника і чотирикутника Урок № 50 Тема: Кути трикутника і чотирикутника Мета. Познайомити учнів з видами кутів і трикутників в залежності від кутів, які входять до кута. Навчити учнів вимірювати кути за допомогою транспортира. Формувати уміння і навички розв’язувати геометричні задачі. Розвивати логічне мислення учнів, шляхом розв’язування задач, продовжувати формувати вміння працювати з підручником. Форми роботи: бліцопитування, робота […]...

  37. Властивість точки, рівновіддаленої від вершин многокутнику Урок 32 Тема. Властивість точки, рівновіддаленої від вершин многокутнику Мета уроку: формування знань про властивість точки, рівновіддаленої від вершин многокутника, та вмінь застосовувати цю властивість до розв’язування задач. Обладнання: стереометричний набір, схема “Коло, описане навколо многокутника”. Хід уроку 1. Перевірити розв’язання задачі № 24 за записами (з пропусками), зробленими на дошці до початку уроку. Розв’язання […]...

  38. РІВНОБЕДРЕНИЙ ТРИКУТНИК РОЗДІЛ 3 ТРИКУТНИКИ & 13. РІВНОБЕДРЕНИЙ ТРИКУТНИК Трикутник називають рівнобедреним, якщо в нього дві сторони рівні. Рівні сторони рівнобедреного трикутника навивають бічними сторонами, а третю його сторону – основою. Трикутник, який не є рівнобедреним, називають різностороннім. Трикутник, у якого всі сторони рівні, називають рівностороннім. Рівносторонній трикутник є окремим видом рівнобедреного трикутника (мал. 166). Рівнобедрений трикутник […]...

  39. Теореми § 2. Трикутники 11. Теореми 269. Теорема Умова Висновок 4.1 Кути АОС і СОВ – суміжні ∠AOC + ∠COB = 180° 8.2 X належить серединному перпендикуляру відрізка AB ХА = ХВ 9.1 ?ABC – рівнобедрений з основою АС 1) ∠A = ∠C; 2) бісектриса кута В є медіаною і висотою 10.3 Два кути трикутника ABC […]...

  40. Описані і вписані кола Розділ 1. Найпростіші геометричні фігури та їх властивості § 17. Описані і вписані кола 671. Коло, описане навколо трикутника, зображено на мал. 372. 672. Коло, вписане у трикутник, зображено на мал. 375. 673. Центр кола, описаного навколо гострокутного трикутника, лежить всередині трикутника. Центр кола, описаного навколо прямокутного трикутника, лежить на середині гіпотенузи. Центр кола, описаного […]...

Ви зараз читаєте: Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника
«
»