Головна ⇒ 📌Довідник з геометрії ⇒ Многокутники
Многокутники
Геометрія
Многокутники
Ламаною 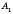
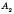
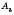 …
…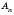 називається фігура, яка складається з точок
називається фігура, яка складається з точок 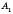 ,
, 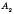 ,
, 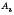 ,…,
,…, 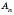 і відрізків, що їх послідовно сполучають. Точки
і відрізків, що їх послідовно сполучають. Точки 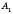 ,
, 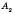 ,
, 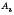 , …,
, …, 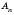 називаються Вершинами ламаної, а відрізки
називаються Вершинами ламаної, а відрізки 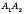
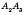 ; …;
; …; 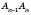 – Ланками ламаної.
– Ланками ламаної.Ламана називається Простою, якщо вона не має самоперетинів. Довжиною ламаної називається сума довжин її ланок.
На рисунку 1 зображена проста ламана, на рисунку 2 – ламана із самоперетином.
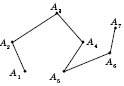
Рис. 1. Проста ламана
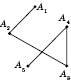
Рис. 2. Ламана із самоперетином
Теорема 1. Довжина ламаної не менша за довжину відрізка, що сполучає її кінці.
Ламана називається Замкненою, якщо її кінці збігаються. Проста замкнена ламана називається Многокутником, якщо
Вершини ламаної називаються Вершинами многокутника, ланки ламаної – Сторонами.
Відрізки, що сполучають несусідні вершини многокутника, називаються Діагоналями.
Многокутник, що має n вершин, називається n-Кутником. n-кутник має
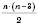 діагоналей.
діагоналей.Многокутник називається Опуклим, якщо він лежить в одній півплощині відносно будь-якої прямої, що містить його сторону.
На рисунку нижче зліва зображений неопуклий многокутник, на рисунку справа – опуклий.
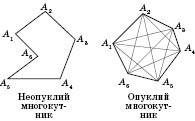
Кутом опуклого многокутника при даній вершині називається кут, утворений сторонами многокутника, що сходяться в цій вершині.
Теорема 2. Сума кутів опуклого n-кутника дорівнює
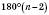 .
.Зовнішнім кутом опуклого многокутника при даній вершині називається кут, суміжний із внутрішнім кутом многокутника при цій вершині.
Теорема 3. Сума зовнішніх кутів опуклого многокутника, узятих по одному при кожній вершині, дорівнює
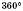 (див. рисунок).
(див. рисунок).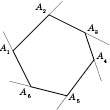
Related posts:
- Правильні многокутники Геометрія Многокутники Правильні многокутники Опуклий многокутник називається Правильним, якщо в нього всі сторони рівні й усі кути рівні. Многокутник називається Вписаним у коло, якщо всі його вершини лежать на деякому колі. Многокутник називається Описаним навколо кола, якщо всі його сторони дотикаються до деякого кола. Теорема 1. Правильний опуклий многокутник є вписаним у коло й описаним […]...
- Правильні многокутники УРОК № 17 Тема. Правильні многокутники Мета уроку: формування поняття правильного многокутника, центра і центрального кута правильного многокутника. Формування вмінь застосовувати вивчений матеріал до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: табл. 4. Вимоги до рівня підготовки учнів: формують означення правильного многокутника; застосовують вивчені означення до розв’язування задач. Хід уроку І. Перевірка домашнього завдання […]...
- Многокутники. Розв’язування задач Урок № 49 Тема: Многокутники. Розв’язування задач Мета. Формувати в учнів уміння і навички самостійно застосовувати вивчений матеріал, до розв’язування задач, розвивати навички самостійної пізнавальної роботи, розвивати вміння самостійної роботи, розвивати вміння аналізувати, робити висновки. Форми роботи: математичний диктант, бесіда, розв’язування задач і виконання вправ. Обладнання: лінійка, кольорова крейда, косинець. Тип уроку: урок узагальнення і […]...
- Сума кутів трикутника Геометрія Основні властивості найпростіших геометричних фігур Сума кутів трикутника Теорема. Сума кутів трикутника дорівнює . Із цієї теореми випливають наслідки: 1. У будь-якому трикутнику принаймні два кути гострі (тобто в трикутнику не може бути більше одного прямого або тупого кута). 2. Кути рівностороннього трикутника дорівнюють . Зовнішнім кутом трикутника при даній вершині називається кут, суміжний […]...
- Многокутники. Розв’язування задач і вправ Урок № 47 Тема: Многокутники. Розв’язування задач і вправ Мета. Дати означення ламаної, ввести поняття многокутника, ознайомити з видами многокутників, видами трикутників за сторонами, формувати навички застосовувати вивчений матеріал до розв’язування задач, сприяти формуванню логічного мислення, виховувати вміння самостійно аналізувати і робити висновки. Форми роботи: самостійна робота з підручником, усне опитування “Мозковий штурм”, метод інтерактивної […]...
- Суміжні й вертикальні кути Геометрія Основні властивості найпростіших геометричних фігур Суміжні й вертикальні кути Два кути називаються Суміжними, якщо в них одна сторона спільна, а інші сторони є доповняльними півпрямими. На рисунку і – суміжні. Властивості суміжних кутів Теорема 1. Сума суміжних кутів дорівнює . (Зверніть увагу: кути, сума яких дорівнює , не обов’язково суміжні.) Теорема 2. Коли два […]...
- Сума кутів опуклого многокутника Урок № 43 Тема. Сума кутів опуклого многокутника Мета: закріпити знання змісту понять, вивчених на попередньому уроці. Працювати над засвоєнням учнями змісту та доведення теореми про суму кутів опуклою многокутника. Сформувати вміння: – відтворювати зміст вивченої теореми; – застосовувати теорему під час розв’язування задач на знаходження градусної міри кутів многокутників. Тип уроку: засвоєння нових знань, […]...
- Многокутники. Рівні фігури Розділ I НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ § 2. ДОДАВАННЯ І ВІДНІМАННЯ НАТУРАЛЬНИХ ЧИСЕЛ 13. Многокутники. Рівні фігури На рисунках 107 і 108 зображено три фігури, кожна з яких обмежена замкненою ламаною, що складається з чотирьох ланок: АВ, ВС, CD і DA. Чим відрізняються межі фігур на рисунку 107 від межі фігури на рисунку […]...
- Ламана і многокутник Урок № 42 Тема. Ламана і многокутник Мета: сформувати в учнів поняття: – ламана та її елементи; – проста ламана; – многокутник та його елементи; – периметр многокутника; – опуклий многокутник; – внутрішній та зовнішній кути многокутника; – многокутник, вписаний у коло та многокутник, описаний навколо кола. Формувати вміння відтворювати означення вивчених понять; на готовому […]...
- Прямокутний трикутник Геометрія Основні властивості найпростіших геометричних фігур Прямокутний трикутник Трикутник називається Прямокутним, якщо він має прямий кут. Сторона, яка лежить проти прямого кута, називається Гіпотенузою. Сторони, що утворюють прямий кут, називаються Катетами. На рисунку – прямокутний. AB і BC – катети, AC – гіпотенуза. Теорема. Сума гострих кутів прямокутного трикутника дорівнює . Ознаки рівності прямокутних трикутників […]...
- Паралелограм Геометрія Чотирикутники Чотирикутником називається фігура, яка складається з чотирьох точок і чотирьох відрізків, що послідовно їх сполучають. При цьому жодні три з даних точок не повинні лежати на одній прямій, а відрізки, які їх сполучають, не повинні перетинатися. Дані точки називаються Вершинами чотирикутника, а відрізки, що їх сполучають,- Сторонами чотирикутника. Вершини чотирикутника називаються Сусідніми, якщо […]...
- Перпендикуляр Геометрія Основні властивості найпростіших геометричних фігур Перпендикуляр Дві прямі називаються Перпендикулярними, якщо вони перетинаються під прямим кутом (див. рисунок), тобто, коли вони перетинаються, утворюються чотири прямих кути. Позначення: . Теорема 1. Через кожну точку прямої можна провести перпендикулярну до неї пряму, і до того ж тільки одну. Перпендикуляром до даної прямої називається відрізок прямої, перпендикулярної […]...
- Тригранний і многогранний кути Геометрія Многогранники Тригранний і многогранний кути Нехай промені a, b, c виходять з однієї точки й не лежать в одній площині. Тригранним кутом називається фігура, яка складається з трьох плоских кутів , , (див. рисунок). Ці кути називаються Гранями тригранного кута, а їх сторони – Ребрами. Спільна вершина плоских кутів називається Вершиною тригранного кута. Двогранні […]...
- Рівнобедрений трикутник Геометрія Основні властивості найпростіших геометричних фігур Рівнобедрений трикутник Трикутник називається Рівнобедреним, якщо у нього дві сторони рівні. Ці сторони називаються Бічними сторонами, а третя сторона – Основою трикутника. На рисунку: ABC – рівнобедрений трикутник; – бічні сторони; AC – основа. Теорема 1. У рівнобедреному трикутнику кути при основі є рівними. Теорема 2. У рівнобедреному трикутнику […]...
- Ромб Геометрія Чотирикутники Ромб Ромб – це паралелограм, у якого всі сторони рівні. Властивості ромба Оскільки ромб є паралелограмом, він має всі властивості паралелограма і деякі інші. Теорема 1. Діагоналі ромба перетинаються під прямим кутом. Діагоналі ромба є бісектрисами його кутів. На рисунку ABCD – ромб; ; ; ; ; . Теорема 2. Діагоналі ромба розбивають […]...
- Рівносторонній трикутник Геометрія Основні властивості найпростіших геометричних фігур Рівносторонній трикутник Якщо всі сторони трикутника рівні, він називається Рівностороннім. На рисунку . Теорема 1. У рівносторонньому трикутнику всі кути рівні. Теорема 2. У рівносторонньому трикутнику висота, медіана, бісектриса, проведені з однієї вершини, збігаються. Теорема 3. У рівносторонньому трикутнику всі медіани (висоти, бісектриси) рівні між собою....
- Квадрат Геометрія Чотирикутники Квадрат Квадрат – це прямокутник, у якого всі сторони рівні. Властивості квадрата Оскільки квадрат є паралелограмом, прямокутником і ромбом водночас, маємо: 1) у квадрата всі сторони рівні; 2) у квадрата всі кути рівні; 3) діагоналі квадрата рівні, перетинаються під прямим кутом, діляться в точці перетину навпіл, є бісектрисами його кутів; 4) діагоналі квадрата […]...
- Перпендикулярність прямих і площин Геометрія Стереометрія Перпендикулярність прямих і площин Дві прямі називаються Перпендикулярними, якщо вони перетинаються під прямим кутом. Теорема 1. Якщо дві прямі, які перетинаються, паралельні відповідно двом іншим перпендикулярним прямим, то інші прямі теж перпендикулярні. Теорема 2. Через будь-яку точку прямої у просторі можна провести безліч перпендикулярних до неї прямих (див. рисунок). (Усі прямі лежать у […]...
- Кут між мимобіжними прямими Геометрія Стереометрія Кут між мимобіжними прямими Дві прямі, що перетинаються, утворюють суміжні та вертикальні кути. Кутова міра меншого із суміжних кутів називається Кутом між прямими. Кут між перпендикулярними прямими дорівнює за означенням. Кут між паралельними прямими вважаємо таким, що дорівнює нулю. Кутом між мимобіжними прямими називається кут між прямими, які перетинаються й паралельні даним мимобіжним […]...
- Кути, вписані в коло Геометрія Кути, пов’язані з колом Кути, вписані в коло Кут розбиває площину на дві частини. Кожна із цих частин називається Плоским кутом. Плоскі кути із спільними сторонами називаються Доповняльними. Якщо плоский кут є частиною півплощини, то його градусною мірою називається градусна міра звичайного кута з тими самими сторонами. Центральним кутом у колі називається плоский кут […]...
- Ознака паралельності прямої і площини Геометрія Стереометрія Ознака паралельності прямої і площини Теорема 1. Якщо пряма, яка не належить площині, паралельна якій-небудь прямій у цій площині, то вона паралельна і самій площині. Теорема 2. Якщо пряма паралельна площині, то на цій площині знайдеться пряма, яка паралельна даній прямій. Зверніть увагу: паралельність прямої і площини не означає, що ця пряма паралельна […]...
- Кут між площинами Геометрія Стереометрія Кут між площинами Кут між паралельними площинами вважається таким, що дорівнює . Нехай дані площини перетинаються (див. рисунок). Проведемо площину, перпендикулярну до прямої їх перетину. Ця площина перетинає дані площини по двох прямих. Кут між цими прямими називається Кутом між даними площинами. Означений таким чином кут між площинами не залежить від вибору січної […]...
- Теорема косинусів Геометрія Розв’язування трикутників Теорема косинусів Теорема (косинусів). Квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін і косинуса кута між ними. У трикутнику, зображеному на рисунку, за теоремою косинусів: . Теорему косинусів зручно застосувати для розв’язування таких задач. 1. Знайти сторону трикутника, якщо відомі дві інші сторони й кут […]...
- Бісектриса Геометрія Основні властивості найпростіших геометричних фігур Бісектриса Бісектрисою кута називається промінь, який виходить із вершини кута, проходить між його сторонами й ділить кут пополам. На рисунку BD – бісектриса . Властивості бісектриси Теорема 1. Бісектриса кута утворює з його сторонами кути, не більші за . Теорема 2. Бісектриси вертикальних кутів лежать на одній прямій (тобто […]...
- ТАБЛИЦІ ДОДАВАННЯ Й ВІДНІМАННЯ ЧИСЛА 9 З ПЕРЕХОДОМ ЧЕРЕЗ ДЕСЯТОК. ПЕРИМЕТР МНОГОКУТНИКА ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ. ЗАДАЧІ НА ДВІ ДІЇ. ВИРАЗИ З ДУЖКАМИ ЗАДАЧІ НА ДВІ ДІЇ Урок 23. ТАБЛИЦІ ДОДАВАННЯ Й ВІДНІМАННЯ ЧИСЛА 9 З ПЕРЕХОДОМ ЧЕРЕЗ ДЕСЯТОК. ПЕРИМЕТР МНОГОКУТНИКА Мета: ознайомити учнів з таблицями додавання і віднімання числа 9 з переходом через десяток; вчити знаходити периметр многокутника; вдосконалювати обчислювальні навички; формувати вміння аналізувати задачі; […]...
- Паралельні прямі Геометрія Основні властивості найпростіших геометричних фігур Паралельні прямі На рисунку зображені кути, утворені в результаті перетину двох прямих січною: і ; і – внутрішні різносторонні кути при прямих a, b і січній c. і ; і – внутрішні односторонні. і ; і – зовнішні односторонні. і ; і – зовнішні різносторонні. і ; і ; […]...
- Прямокутник Геометрія Чотирикутники Прямокутник Прямокутник – це паралелограм, у якого всі кути прямі. Властивості прямокутника Оскільки прямокутник є паралелограмом, він має всі властивості паралелограма і ще деякі інші. Теорема. Діагоналі прямокутника рівні. На рисунку . . ; – рівнобедрені. Ознаки прямокутника Теорема 1. Якщо в чотирикутнику всі кути рівні, то він є прямокутником. Теорема 2. Якщо […]...
- Коло Геометрія Основні властивості найпростіших геометричних фігур Коло Колом називається фігура, яка складається з усіх точок площини, рівновіддалених від даної точки. Ця точка називається Центром кола. Відстань від точок кола до його центра називається Радіусом кола. Радіусом також називається будь-який відрізок, що сполучає точку кола з його центром. Відрізок, що сполучає дві точки кола, називається Хордою. […]...
- Теорема про триперпендикуляри Геометрія Стереометрія Теорема про триперпендикуляри Теорема 1. Якщо пряма, проведена на площині через основу похилої, перпендикулярна до її проекції, то вона перпендикулярна до похилої (див. рисунок). І навпаки: якщо пряма на площині перпендикулярна до похилої, то вона перпендикулярна і до проекції похилої. Приклади застосування теореми про три перпендикуляри 1. На рисунку – куб. , тому […]...
- Теорема Фалеса Геометрія Чотирикутники Теорема Фалеса Теорема 1 (Фалеса). Якщо паралельні прямі, які перетинають сторони кута, відтинають на одній його стороні рівні відрізки, то вони відтинають рівні відрізки й на другій його стороні. На рисунку ; ; . Зверніть увагу: . Теорема має місце не тільки для сторін кута, а й для довільних прямих. Теорема 2 (про […]...