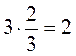Множення звичайних дробів
Урок № 2 5
Тема. Множення звичайних дробів
Мета: на основі сформованих на попередньому уроці знань і вироблених умінь виконувати множення звичайних дробів; сформувати уявлення і виробити відповідні вміння виконувати множення натурального числа на звичайний дріб та множення мішаних чисел.
Тип уроку: засвоєння нових знань.
Хід уроку
І. Перевірка домашнього завдання
@ На перерві перевіряються зошити “слабких” учнів (наявність домашнього завдання можуть допомогти вчителеві перевірити чергові). На уроці – фронтально
Математичний диктант
Варіант 1 | Варіант 2 |
1. Виконайте множення: 1) 2. Знайдіть добуток: 1) | 1. Виконайте множення: 1) 2. Знайдіть добуток: 1) |
II. Актуалізація
@Повторення знань, пов’язаних із множенням звичайних дробів, відбувається під час перевірки і аналізу помилок, яких припустилися учні під час виконання завдань математичного диктанту. Тому перед викладенням навчального матеріалу цього уроку слід зосередити увагу учнів на:
– перетворенні мішаного числа у неправильний дріб;
– натурального числа у неправильний дріб.
Усні вправи
1. Знайдіть серед записаних чисел зайве: 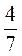 ;
; 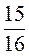 ;
;  ;
; 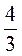 .
.
2. Серед чисел, що записані нижче, знайдіть пари рівних: 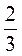 ;
; 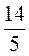 ;
; 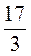 ;
; 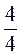 ;
; 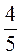 ; 1;
; 1; 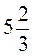 ;
; 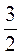 .
.
3. Перетворіть у неправильний дріб числа: 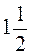 ;
; 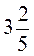 ; 1; 2; а.
; 1; 2; а.
III. Засвоєння знань учнів
@ Після виконання усних вправ на повторення (див. вище) майже всі учні готові до сприйняття матеріалу. Бо твердження “мішане число можна записати звичайним дробом” і “натуральне число можна записати звичайним дробом” вже не викликають сумнівів, тому залишається завершити логічний ланцюжок висловом:
Щоб помножити натуральне число / мішане число на звичайний дріб, треба перетворити натуральне число / мішане число у неправильний дріб, а потім виконувати множення звичайних дробів (конспект 14).
Але ж після виконання кількох прикладів “сильні” учні можуть помітити (на це треба їх націлити), а якщо вони не впораються, допомогти їм “побачити”, що: 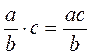 .
.
Щоб помножити дріб на натуральне число, треба його чисельник помножити на це число, а знаменник залишити без змін.
Краще, якщо результати міркувань будуть записані учнями у вигляді конспекту № 15.
Конспект 15 | |
Особливі випадки множення дробів | |
1. Множення мішаних чисел @ Перетворіть мішане число у неправильний дріб і виконайте множення звичайних дробів. 2. Множення звичайного дробу
| Приклад А) Приклад А) |
IV. Формування вмінь
І рівень
Усні вправи
Виконайте множення: а) 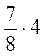 ;
; 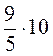 ;
; 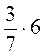 ; б)
; б) 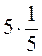 ;
; 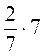 ;
; 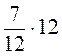 ; в)
; в) 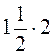 ;
; 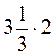 ;
; 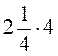 ; г)
; г) 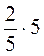 ;
; 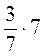 ;
; 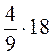 .
.
ІІ, III рівні
Письмові вправи
1. Обчисліть: а) 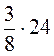 ; б)
; б) 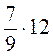 ; в)
; в) 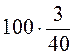 ; г)
; г) 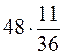 .
.
2. Обчисліть: а) 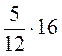 ; б)
; б) 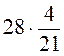 .
.
3. Обчисліть: а) 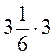 ; б)
; б) 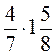 ; в)
; в) 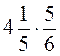 ; г)
; г) 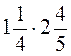 ; д)
; д) 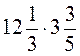 ; е)
; е) 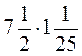 ; ж)
; ж) 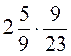 ; з)
; з) 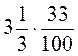 ; и)
; и) 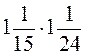 ; к)
; к) 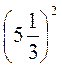 .
.
4. Спростіть вираз: а) 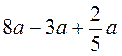 ; б)
; б) 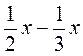 ; в)
; в) 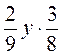 .
.
5. Розв’яжіть рівняння 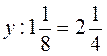 .
.
6. Обчисліть: а) 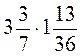 ; б)
; б) 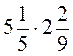 .
.
7. Обчисліть: а) 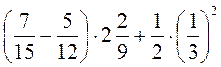 ; б)
; б) 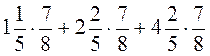 .
.
8. Обчисліть добуток: а) 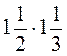 ; б)
; б) 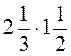 ; в)
; в) 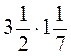 ; г)
; г) 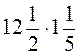 ; д)
; д) 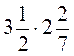 ; е)
; е) 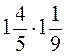 .
.
9. Обчисліть значення виразів: а) 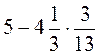 ; б)
; б) 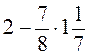 ; в)
; в) 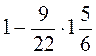 .
.
10. Обчисліть значення виразів: а) 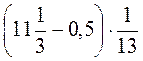 ; б)
; б) 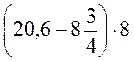 .
.
11. Обчисліть значення виразів: а) 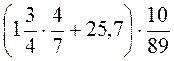 ; б)
; б) 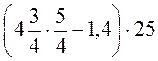 .
.
Додаткові завдання
1. 1 кг пряників коштує 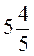 грн. Скільки коштують
грн. Скільки коштують 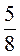 кг; 2кг;
кг; 2кг; 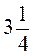 кг пряників?
кг пряників?
2. За формулою s = vt знайдіть s, якщо: a) v = 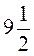 км/год, t =
км/год, t = 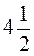 год; б) v =
год; б) v = 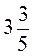 м/хв; t =
м/хв; t = 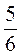 хв.
хв.
3. Знайдіть масу металевої деталі, якщо її об’єм 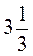 дм, а маса 1 дм3 цього металу
дм, а маса 1 дм3 цього металу 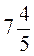 кг.
кг.
4. Два велосипедисти виїхали одночасно з одного й того самого міста в одному напрямку. Швидкість одного з них 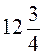 км/год, а іншого – у
км/год, а іншого – у 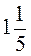 рази більша. Яка відстань буде між ними через
рази більша. Яка відстань буде між ними через 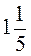 Год?
Год?
5. З першого поля, площа якого 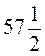 га, зібрали з 1 га по
га, зібрали з 1 га по 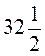 ц пшениці, а з другого поля, площа якого у
ц пшениці, а з другого поля, площа якого у 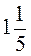 рази більша за площу першого поля, зібрали по
рази більша за площу першого поля, зібрали по 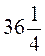 ц пшениці з 1 га. Скільки всього центнерів пшениці зібрали з цих двох полів?
ц пшениці з 1 га. Скільки всього центнерів пшениці зібрали з цих двох полів?
V. Підсумки уроку
– Як помножити два звичайні дроби?
– Як помножити натуральне число на звичайний дріб?
– Як помножити мішане число на будь-яке число?
VI. Домашнє завдання
1. Обчисліть (усно): а) 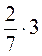 ; б)
; б) 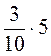 ; в)
; в) 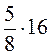 ; г)
; г) 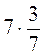 .
.
2. Обчисліть: а) 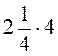 ; б)
; б) 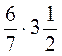 ; в)
; в) 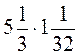 ; г)
; г) 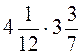 ; д)
; д) 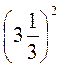 .
.
3. Розв’яжіть рівняння 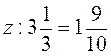 .
.
4. Знайдіть добуток суми чисел 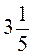 і
і 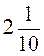 та їх різниці.
та їх різниці.
5. Обчисліть: а) 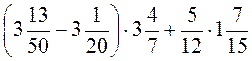 ; б)
; б) 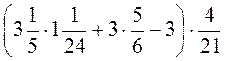 .
.
6. Поле площею 240 га засіяли горохом і гречкою, причому горохом засіяли 0,4 площі поля. Скільки гектарів поля засіяли гречкою?
7. Обчисліть добутки: а) 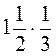 ; б)
; б) 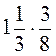 ; в)
; в) 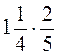 ; г)
; г) 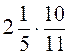 ; д)
; д) 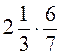 ; е)
; е) 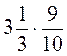 .
.
8. Обчисліть значення виразів: а) 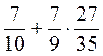 ; б)
; б) 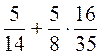 ; в)
; в) 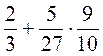 ; г)
; г) 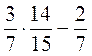 .
.
9. Спростіть вираз: а) 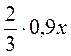 ; б)
; б) 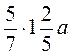 ; в)
; в) 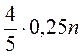 ; г)
; г) 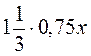 .
.
10. На скільки площа квадрата зі стороною 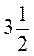 м більша за площу квадрата зі стороною
м більша за площу квадрата зі стороною 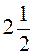 М?
М?
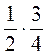 ; 2)
; 2) 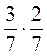 ; 3)
; 3) 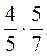 ; 4)
; 4) 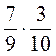 .
.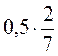 ; 2)
; 2) 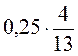 .
.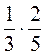 ; 2)
; 2) 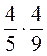 ; 3)
; 3) 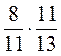 ; 4)
; 4) 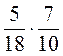 .
.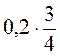 ; 2)
; 2) 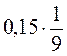 .
.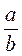 на натуральне число с
на натуральне число с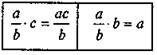
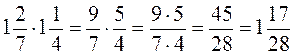 ; б)
; б) 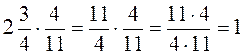 .
.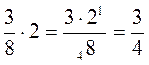 ; б)
; б) 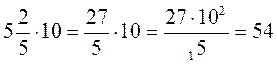 ; в)
; в) 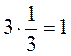 ;
;