Об’єм конуса і зрізаного конуса
1295.
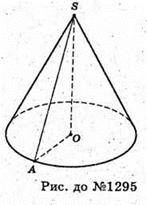
Нехай SA – твірна конуса, ∠SAO = α, SA = l.
З ΔSAO : SO = SA × sin ∠SAO = I sin α,
AO = AS × cos ∠SAO = І × cos α.
Отже, об’єм конуса V дорівнює:
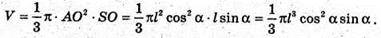
Відповідь: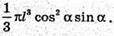 
1296.
Нехай радіус основи свинцевого конуса дорівнює r, а висота циліндра – H.
Об’єм V конуса: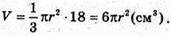 
Об’єм V1циліндра: V1 = πr2H.
Прирівняємо праві частини 6πr2 = πr2H, звідси H = 6 (см).
Відповідь: 6 см.
1297.
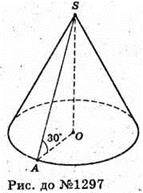
З геометричної точки
∠SAO = 30°.
З ΔSAO: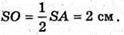 
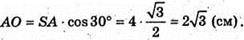
Отже, об’єм V конуса дорівнює:
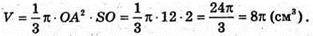
Відповідь: 8π (см3).
1298.
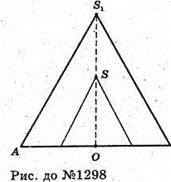
На рисунку зображено осьовий переріз конусів. Оскільки кут природного ухилу зберігається, то, якщо висота одного конуса вдвічі більша, то і радіус вдвічі більший.
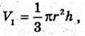
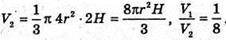
Отже у першому конусі зерна у 8 разів більше, ніж у другому.
1299.
Нехай виміри першого конуса: г – радіус основи, h – висота конуса; виміри
Об’єм V1першого конуса: V1 = πr2h.
Об’єм V2другого конуса: V2 = πk2r2× kh = πk2r2h.
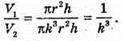
1300.
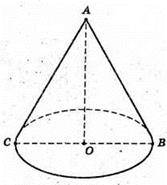
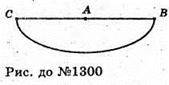
Як видно з рисунка, радіус півкола AB є твірною конуса.
Знайдемо радіус конуса із співвідношення:
π × AB = 2π × OB, звідси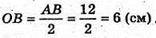 
З ΔAOB: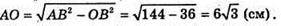 
Отже, об’єм конуса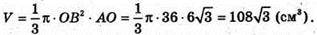 
Відповідь: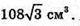 
1301.
Нехай в основі правильної, трикутної піраміди лежить трикутник зі стороною a, тоді радіус основи конуса, вписаного в піраміду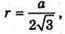 
а радіус основи конуса, описаного навколо піраміди, 
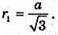h – висота піраміди, а також і висота вписаного і описаного конусів.
Знайдемо V1об’єм вписаного конуса: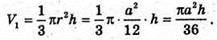 
Знайдемо V2об’єм описаного конуса: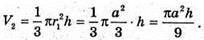 
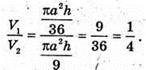
1302.
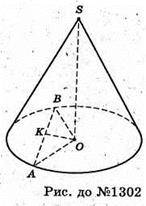
Нехай SA – твірна конуса, ∠ASO = α. AB = m,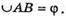 
Оскільки ∠BOA – центральний кут, то ∠BOA = φ.
В рівнобедреному МОВ: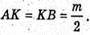 
Проведемо OK + AB.
З ΔAKO: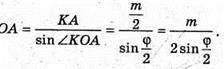 
З ΔSAO: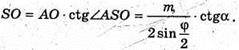 
Отже, об’єм конуса дорівнює:
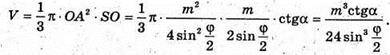
Відповідь: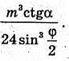 
1303.
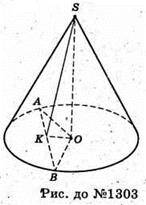
Проведемо площину SAB. В цій площині проведемо SK + AB. Тоді за теоремою про три перпендикуляри OK + AB, отже, ∠SKO = 45°, AB = a, ∠AOB = 60°.
ΔAОВ рівнобедрений (оскільки OA = OB як радіуси основи).
OK – висота ΔAOB, а також бісектриса і медіана.
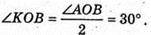
З ΔKOB: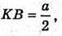 
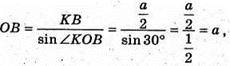
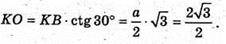
Розглянемо ΔSKO: оскільки ∠SKO = 45°, то і ∠KSO = 45° і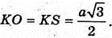 
Отже, об’єм V конуса дорівнює: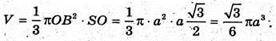 
Відповідь: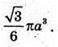 
1304.
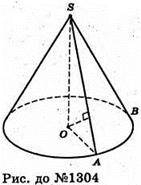
Нехай SA – твірна конуса, OB + SA, OB = d, ∠ BOA = α.
З ΔOBA: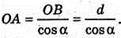 
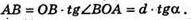
За властивістю висоти прямокутного трикутника маємо:
OB2 = AB × SB, d2 = d × tgα × SB, звідси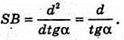 
З ΔSOB: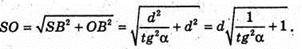 
Отже, об’єм V конуса дорівнює:
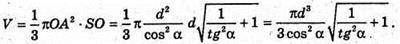
Відповідь: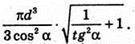 
1305.
Нехай SAB – осьовий переріз, SA = AB = SB, Sпов. =12πсм2.
Нехай SB – твірна, OB – радіус SB = I, OB = г, тоді S = πR(R + l).
Оскільки ΔSAB рівносторонній,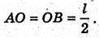 
Отже,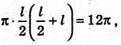 
3l2 =48, l2 =16, l = 4,
Тобто SB = 4 см, OB = 2 см.
З ΔSOB: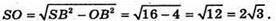 
Отже, об’єм конуса дорівнює:
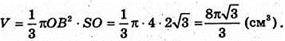
Відповідь: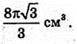 
1306.
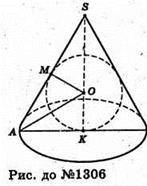
Нехай MO – радіус вписаної кулі, MO = r, ∠SAK = α.
ΔMOA = ΔKOA (за гіпотенузою і катетом: AO – спільна гіпотенуза, OM = OK).
Отже,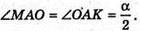 
З ΔAOK: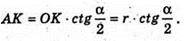 
З ΔSAK: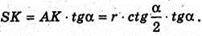 
Отже, об’єм конуса V дорівнює:
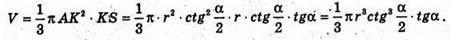
Відповідь: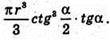 
1307.
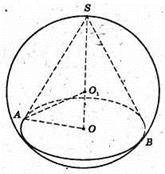
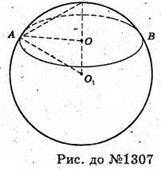
SO1 = O1A = 2r – радіус кулі, AO – радіус основи конуса, AO = г.
З ΔO1AO: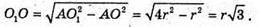 
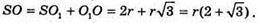
Знайдемо V – об’єм конуса:
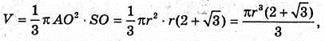
Або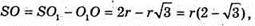 
Тоді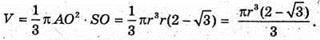 
Відповідь: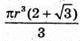 
або 
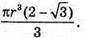
1308.
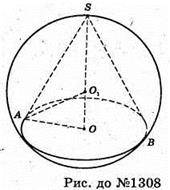
Нехай SAB – осьовий переріз конуса, вписаного в сферу, SO1 = AO1 = r,
∠ASO = α.
За теоремою синусів для ΔASB: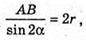 
Звідси AB = 2г sin 2α, AO = r sin 2α.
3 ΔSAO: SO = AO × ctgα = r sin 2α ctgα = 2r cos2 α.
Отже, об’єм V конуса:
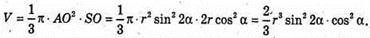
Відповідь: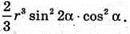 
1309.
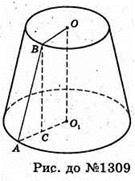
Нехай OB і O1A – радіуси основ зрізаного конуса O1A = 16 см, OB = 10 см,
∠BAC = 45°.
Проведемо BC + AO1, тоді AC = AO1 = CO1 =16 – 10 = 6 (см).
З ΔABC оскільки ∠BAC = 45°,тоі ∠ABC = 45°, тобто ΔABC — рівнобедрений.
BC = AC = 6 см.
Отже, об’єм V зрізаного конуса дорівнює:
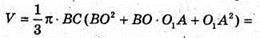
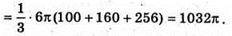
Відповідь: 1032π.
1310.
Нехай H – висота зрізаного конуса і циліндра.
Об’єм V зрізаного конуса: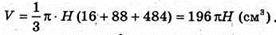 
Об’єм циліндра: V1 = πr2H, де r – радіус основи циліндра.
V = V1; 196 πН = πr2H, звідси г2 = 196, г = 14 (см).
Відповідь: 14 см.
1311.
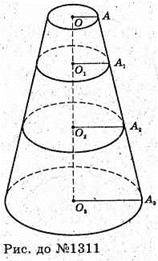
Оскільки через точки O1, O2проведені площини паралельні основам,
То OA? O1A1? O2A2? O3A3 і за теоремою Фалеса AA1 = A1A2 = A2A3,
OO1= O1O2 = O2O3 = 6 (см) .
Розглянемо чотирикутник O1A1A3O3 – це трапеція.
O2A2- середня лінія трапеції, отже,
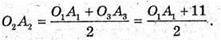
Розглянемо трапецію OAA2O2:
О1А1 – середня лінія трапеції, отже,
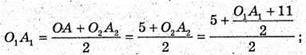
4O1A1 = 10 + O1A1 +11; 3O1A1 =21; O1A1 = 7 см ;
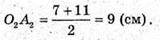
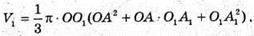
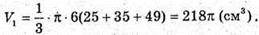
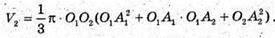
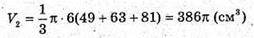
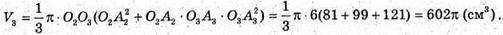
Відповідь: 218π см3, 386π см3 , 602π см3 .
1312.
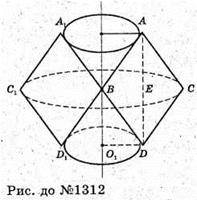
Нехай ромб ABCD обертається навколо прямої a, CB + a.
З ΔABE : BE = AB × sin ∠BAE = 6 × sin 30° = 3 (см), BC = 2ВЕ = 6 см.
При обертанні ромба ABCD навколо прямої а утвориться фігура, яка складається з двох зрізаних конусів (r1 = OA, R = BC, r2 = O1D), з яких вийняті
Конуси (г1 = OA, H1 = OB, г2 = O1D, H2 = BO1).
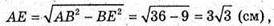
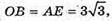OA = BE = 3.
V1- об’єм зрізаного конуса:
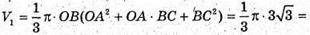
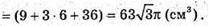
Оскільки обидва зрізаних конуси рівні, то і V2 – об’єм другого зрізаного конуса
Теж дорівнює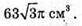 
V3- об’єм конуса з радіусом основи OA і висотою OB дорівнює:
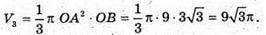
Оскільки об’єми конусів рівні, то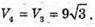 
Знайдемо об’єм утвореної фігури:
Відповідь: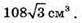 
1313.
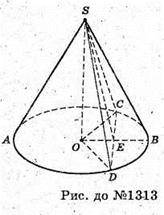
Нехай SC і SD – твірні, конуса, SC = SD = І, ∠COD = β.
Проведемо SE + CD, OE – проекція SE, отже, за теоремою про три перпендикуляри OE + CD, отже, ∠SEO = α. Нехай OD = г.
З ΔSOD: SO2 = SD2 – OD2 = l2 – г2.
З ΔOED: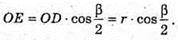 
З ΔSOE: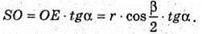 
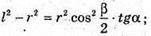
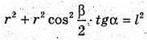
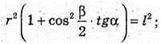
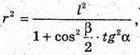
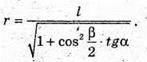
Отже, об’єм конуса:
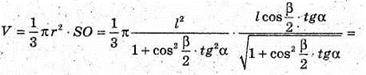
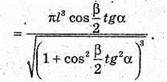
Відповідь: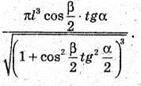
1314.
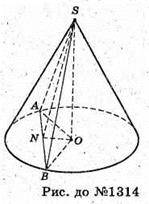
Нехай SA і SB – твірні конуса. SAB – січна площина, ∠ASB = α, SAB = Q.
Проведемо SN + AB, тоді за теоремою про три перпендикуляри ON + AB,
Отже, ∠SNO = β. Позначимо AB = 2х.
З ΔASN: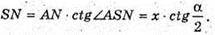 
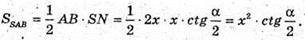
З іншого боку, SSAB = Q, отримаємо
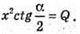
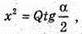
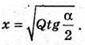
3 ΔSNO: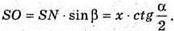 
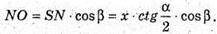
З ΔNOB: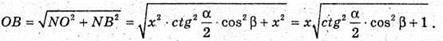 
Отже, об’єм V конуса дорівнює:
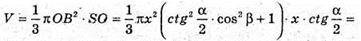
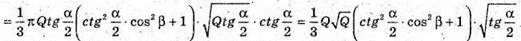
Відповідь: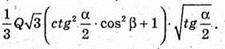 
1315.
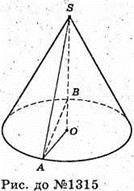
Нехай SAB – січна площина, AB = OB = OA = г. Оскільки AB = OB = OA, то ∠BOA = 60° ,
Основа циліндра розбилася на два сектори, один з кутом 60°, а другий 300°..
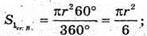
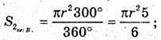
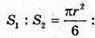
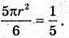
Оскільки висота отриманих частин однакова, то об’єми будуть відноситься також як площі основ, тобто 1 : 5.
1316.
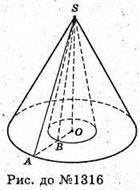
Нехай в конусах S – спільна висота, SO = h,
∠SBO = α. ∠ASB – ∠BSO = β, ∠ASB = x.
З ΔSBO: ∠BSO = 90° – α . х – 90° + α = β, х = β + 90° – α.
∠ASB = β + 90° – α.
∠ASO = ∠ASB + ∠BSO = β + 90° – α + 90° – α = 180° + β – 2α,
З ΔSBO: BO = SO × ctg∠SBO = h × ctgα.
З ΔSAO: AO = SO × tg∠ASO = h × tg(180 + β – 2α) = h × tg(β – 2α).
Отже,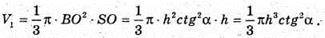 
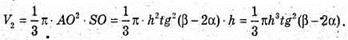
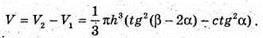
Відповідь: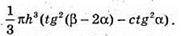 
1317.
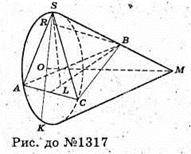
Нехай в піраміді SABC SC = SB = SA = 10 см, AB = BC = AC =16 см.
Знайдемо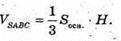 
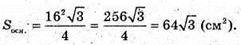
Нехай R – радіус кола, описаного навколо ΔABC.
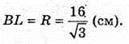
3 ΔSBL: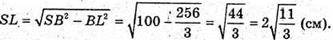 
Отже,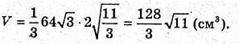 
Знайдемо SΔSCA = 48 (см2).
Радіус кола, описаного навколо ΔSAC:
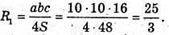
Знайдемо об’єм піраміди з вершиною в точці В і основою SAC:
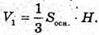
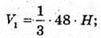
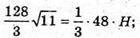
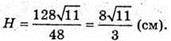
З ΔSPB: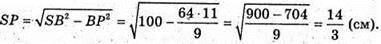 
ΔSPB ~ ΔSOM.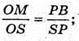 
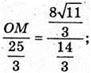
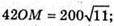
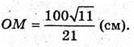
Отже, об’єм конуса:
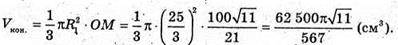
Відповідь: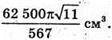 
1318.
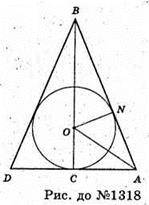
Нехай BDA – осьовий переріз конуса, в який вписано кулю,
ON = r, ∠BOA = α, тоді ∠AOC = 180° – α, ∠CAO = 90° – (180° – α) = α – 90°,
∠CAB = 2∠CAO = 2α – 180°.
З ΔОАС: AC = OC × tg(180 – α) = – OC × tgα = – r × tg α.
З ΔBCA: BC = AC × tg(2α – 180°) = AC × tg 2α = – г × tg α × tg 2α.
Отже, об’єм конуса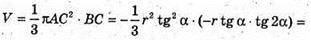 
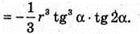
Відповідь: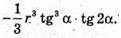 
1319.
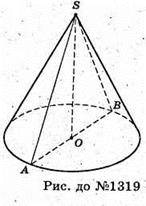
Нехай SAB – осьовий переріз. Psab = 10 дм, AB = d.
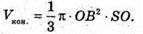
Psab = SA + SB + АВ; 10 = 2SA + d;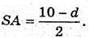 
З ΔSAO: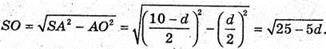 
Отже,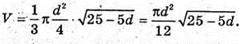 
Дослідимо функцію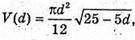 
Де d? [0; 5].
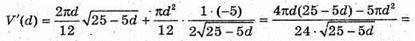
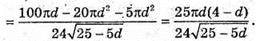
V′(d) = 0; d(4 – d) = 0; d = 0 або d = 4.
Оскільки V(0) = 0,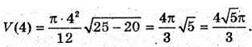 
V(5) = 0, то найбільше значення об’єму конуса дорівнює
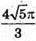при d = 4 дм.
Відповідь: d = 4 дм.
1320.
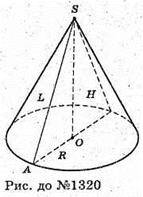
Нехай площа бічної поверхні конуса дорівнює S,
Тоді S = πRL, або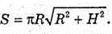 
Нехай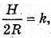 
тоді H = 2Rk i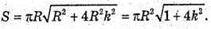 
Тоді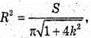 
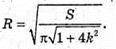
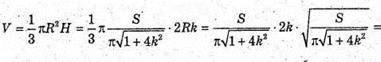
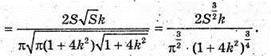
Дослідимо функцію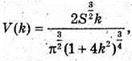 
Де k? (0; +∞), на найбільше значення*
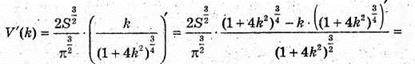
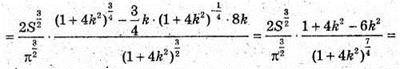
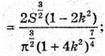
V′(k) = 0; 1 – 2k2 = 0; 2k2 = 1;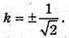 
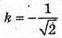не належить проміжку (0; +∞).
Тоді: якщо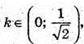 
то V′(k) > 0,
V(k) – зростає на проміжку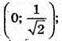 
Якщо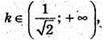 
то V′(k) < 0, V(k) – спадає на проміжку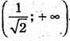 
Отже,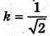 
– єдина точка максимуму функції V(k) на проміжку (0; +∞), тоді найбільше значення функції V(X) на проміжку (0; +∞) досягається в точці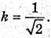 
Отже, відношення висоти конуса до діаметра дорівнює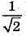 
І при цьому значенні конус має найбільший об’єм при заданій площі бічної поверхні.
Відповідь: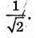 
1321.
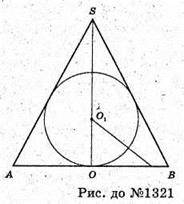
Нехай трикутник ABC з вписаним колом – осьовий переріз конуса, описаного навколо кулі. O1O = г,
∠SBO = α,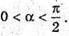 
З ΔBOO1: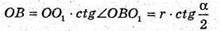 
З ΔSBO: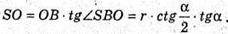 
Об’єм конуса: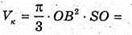 
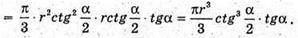
Розглянемо функцію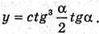 
(1)
Зрозуміло, що при тих же значеннях α, при яких у = ymin, V = Vк. min.
Знайдемо похідну функції (1):
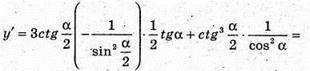
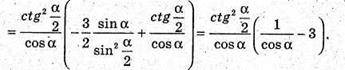
Враховуючи, що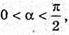 
знаходимо критичну точку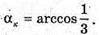 
При переході а через критичну точку від менших значень до більших, різниця
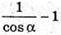змінює знак з “-” на “+”.
Отже, функція (1) в точці α. приймає мінімальне значення.
Обчислимо його:
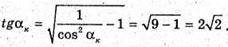
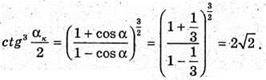
Отже,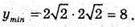 
Таким чином,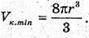 
Відповідь: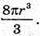 
1322.
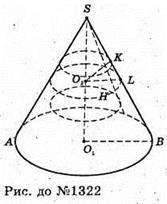
Нехай O1O2- радіус вписаної кулі, ∠KO2L = 60°, O1O2 = r, O2K + SB (як радіус, проведений в точку дотику).
∠SO2K = 90° – ∠KO2L = 90° – 60° = 30°.
3 ΔSO2K: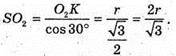 
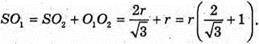
З ΔSO1B: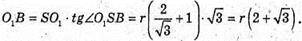 
Отже, об’єм конуса V дорівнює:
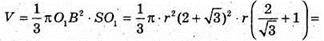
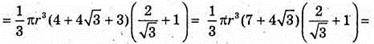
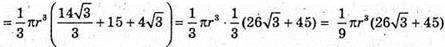
Відповідь: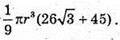 
1323.
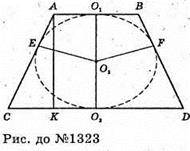
Нехай O1A = r1, O2C = r2, O1O = г.
З ΔACK : CK2 = CA2- AK2, оскільки CK = г2 – г1, то маємо:
(r2- r1) = (г1 + г2)2 = 4r2 – 2r1r2 = 2г1г2 – 4г2; 4г1r2 = 4г2; r1r2 = r2.
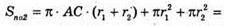
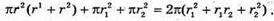
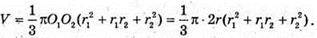
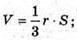3V = r × S.
Відповідь: SV = r × S
1324.
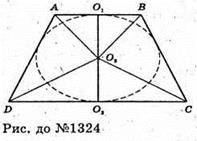
Нехай O1O3- радіус вписаної кулі O1O3 = г, ∠DO3C = α.
З ΔO3O2D: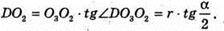 
∠AO2D= 90° (оскільки DO3і AO3 бісектриса кутів O і А).
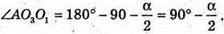
З ΔAO1O3: 
Отже, об’єм V зрізаного конуса дорівнює:
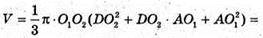
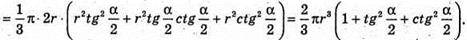
Відповідь: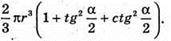 
1325.
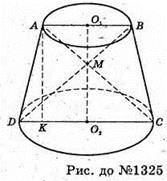
Нехай ABCD – осьовий переріз, AC + BD, AD = l, ∠ADC = α.
З ΔAKD: AK = AD × sin∠ADK = І × sinα.
Оскільки ΔDMC – прямокутний, ∠M = 90°, а DM = MC, то ΔDMC – рівнобедрений. ∠MDC = ∠MCD = 45°, Отже, ∠ADM = a-45°.
З ΔAMD: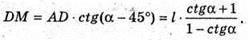 
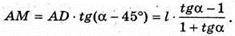
З ΔDMC: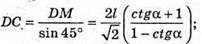 
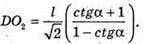
З ΔAMB: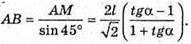 
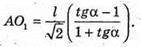
Отже, об’єм конуса V :
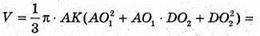
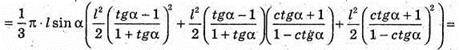
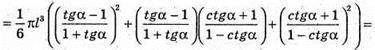
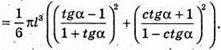
Відповідь: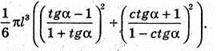 
1326.
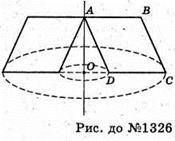
Нехай ABCD – ромб, AB = BC = CD = AD = а, ∠BAD = α.
При обертанні ромба навколо прямої утвориться фігура, яка складається зі зрізаного конуса (R = OC, r = AB ), з якого витягнутий конус (г1 = OD).
Оскільки ∠BAD = α, то ∠OAD = 90° – α.
З ΔAOD: AO = AD × cos(90° – α) = AD × sin α = а × sin α.
OD = AD × sin(90° – α) = AD × cos α = а × cos α.
OC = OD + DC = a cos α + а = а(1 + cos α).
Знайдемо V1- об’єм конуса:
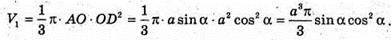
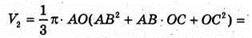
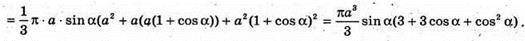
Об’єм утвореної фігури;
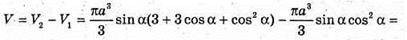
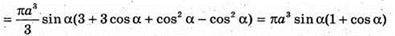
Відповідь: πа3 sin α(1 + cos α).
1327.
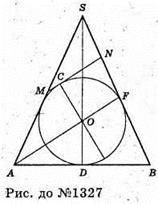
Трикутник ASB – осьовий переріз конуса. Відрізок MN – перетин осьового перерізу конуса з перерізом конуса площиною, заданою в умові задачі, отже, MN + SD. OD = r, SN = d. CNFO – квадрат → NF = г.
Позначимо ∠SAD = SOF = 2α, тоді SD = AD × tg2α.
Маємо: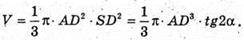 
З ΔAOD: AD = OD × ctg α (оскільки AO – бісектриса ∠SAD).
AD = г × ctgα, тоді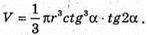 
З ΔSOF: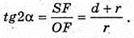 
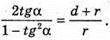
Г × 2tgα = (d + r)(1 – tg2α). (d + г) × tg2α + 2rtgα – (d + r) = 0 .
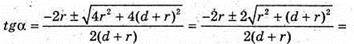
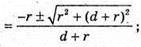
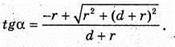
Отже, маємо:
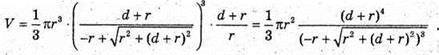
Відповідь: 
(1 votes, average: 5.00 out of 5)
Loading...