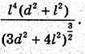Об’єм піраміди і зрізаної піраміди
1247.
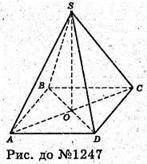
Нехай SABCD – правильна піраміда.
SA = SB = SC = SD = AB = BC = CD = AD = 1 дм.
З ΔACD: 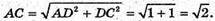
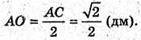
З ΔSAO: 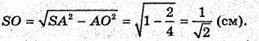
Знайдемо об’єм піраміди
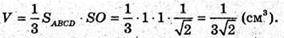
Відповідь: 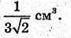
1248.
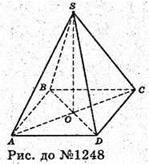
Нехай SABCD – правильна чотирикутна піраміда, SAC – діагональний переріз, SA = SC = AC = а.
З ΔASO: 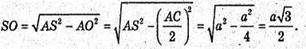
Отже, об’єм піраміди: 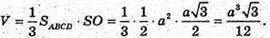
Відповідь: 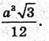
1249.
Об’єм
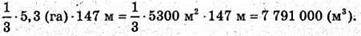
Відповідь: 7 791 000 м3.
1250.
Перевернемо піраміду SABC, прийнявши за основу грань SAB,
Тоді 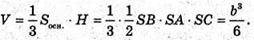
Відповідь: 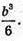
1251.
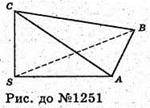
Нехай в піраміди SABC бічні ребра SA = а, SB = b, SC = с.
Приймемо за основу піраміди одну з бічних граней, наприклад SAB.
Тоді основою такої піраміди буде прямокутний трикутник SAB, а висотою SC.
Об’єм V такої піраміди дорівнює:
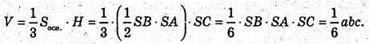
Відповідь: 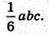
1252.
Нехай SABCD — правильна чотирикутна піраміда, SA = SB = SC = SD = b.
A) ∠SAO = α. З ΔSAO: SO = SA × sin α = b × sin α; AO = SA × cos α = b × cos α.
Об’єм V піраміди дорівнює: 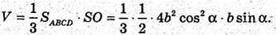
Відповідь: 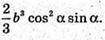
Б) ∠ACO = β,3 ΔSAO: SO = SA ∠ cos β = b cos β; AO = SA × sin β = b × sin β.
Об’єм V піраміди дорівнює: 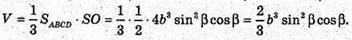
Відповідь: 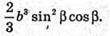
В) ∠SAD = γ. Проведемо SK + AD.
З ΔASK: SK = AS × sin ∠SAD = b × sin γ;
AK = AS × cos ∠SAD = AS × cos γ = b × cos γ; AK = OK = b cos γ; AB = 2b cos γ.
3 ΔSKO: 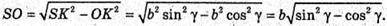
Об’єм V піраміди дорівнює:
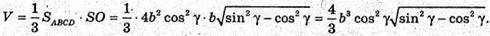
Відповідь: 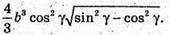
1253.
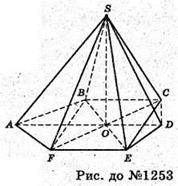
Нехай SEC – заданий переріз в піраміді SABCDEF.
Позначимо а – сторона основи, H – висота піраміди.
Площа основи першої частини
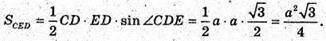
Оскільки площа правильного шестикутника дорівнює 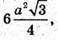
То площа основи другої частини 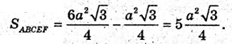
Об’єм V1першої частини дорівнює:
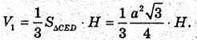
Об’єм V2другої частини дорівнює:
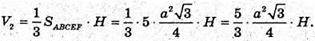
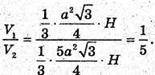
Відповідь: 1 : 5.
1254.
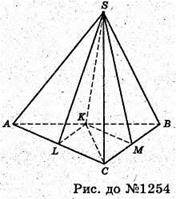
Нехай SABC – задана піраміда, AB = BC = CA = а.
Проведемо SK + АВ, SM + СВ, SL + АС, тоді за теоремою про три перпендикуляри CK + АВ, MK + СВ, KL + AC, ∠SKC = 90°, ∠SLK = ∠SMK = 45°. Оскільки ∠SKC = 90°, то SK буде висотою піраміди.
З ΔАКС: 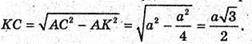
ΔACK – ΔLKA, звідси: 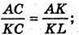
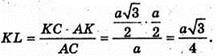
ΔSKL, оскільки ∠SLK = 45°, то 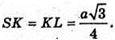
Отже, об’єм піраміди V дорівнює:
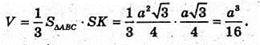
Відповідь: 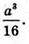
1255.
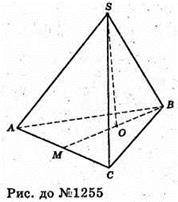
Нехай SABC – правильний тетраедр. AB = BC = AC = SA = SB = SC = а.
Площа Socн. основи тетраедра дорівнює 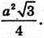
BM – медіана, висота і бісектриса.
Нехай SO – висота, тоді 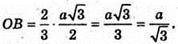
З ΔSOB: 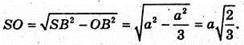
Отже, шуканий об’єм: 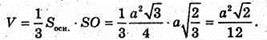
Відповідь: 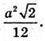
1256.
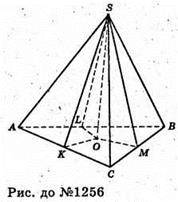
Нехай SABC – задана піраміда, AB = 13 см, BC = 14 см, AC = 15 см.
SO + (ABC), проведемо SK + AC, SM + BC, SL + AB, тоді за теоремою про три перпендикуляри OK + АС, OM + ВС, OL + AS, отже, ∠SKO = ∠SMO = ∠SLO. Оскільки двогранні кути при основі рівні, то вершина проектується в точку O – центр вписаного кола в ААВС.
Об’єм призми 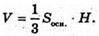
Обчисливши напівпериметр р основи 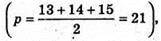 площу основи знайдемо за формулою Герона:
площу основи знайдемо за формулою Герона:
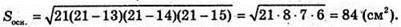
Радіус кола, вписаного в трикутник дорівнює: 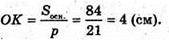
З ΔSKO: H = SO = OK × tg 45° = 4 (см). Тоді 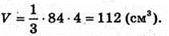
Відповідь: 112 см3.
1257.
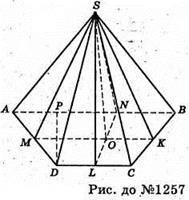
Нехай SABCD – задана піраміда, ABCD – трапеція,
AD = BC = 7 см, AB = 10 см, DC = 4 см. Проведемо SK + CB, SL + DC, SM + AD, SL + AB, тоді за теоремою про три перпендикуляри OK + CS, ON + АВ,
OM + AD, OL + DC.
Оскільки двогранні кути при основі рівні, то вершина проектується в точку O – центр вписаного в трапецію кола.
Розглянемо основу – трапецію ABCD.
Проведемо висоту DP. 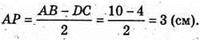
З ΔAPD: 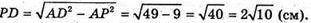
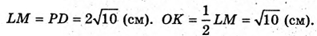
З ΔSOK: 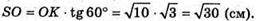
Тоді об’єм V піраміди дорівнює:
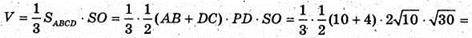
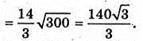
Відповідь: 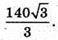
1258.
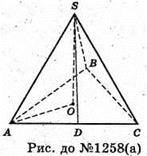
А) Нехай SABC – задана піраміда. AB = BC = АС, SA = SB = SC = b,
∠ABS = ∠ASB = ∠BSC = 2а.
У ΔASC проведемо SK + АС, оскільки трикутник рівнобедрений, то SD буде і бісектрисою. 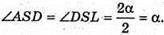
З ΔASD: AD = SA × sin α = b × sin α; тоді AC = 2b sin α. Оскільки в основі лежить правильний трикутник, то вершина S проектується в центр O трикутника.
Знайдемо OA – радіус описаного кола: 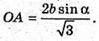
З ΔSAO: 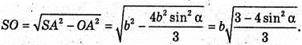
Отже, об’єм V піраміди дорівнює:
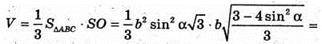
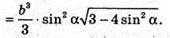
Б)
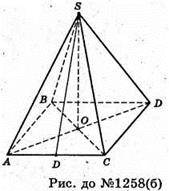
Аналогічно пункту а) знаходимо AC – сторону квадрата. AC = 2b sin α.
Знайдемо OA – радіус описаного кола: 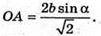
З ΔSAO: 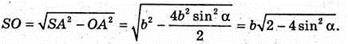
Отже, об’єм V піраміди дорівнює:
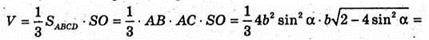
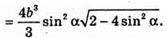
В)
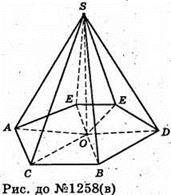
Аналогічно пункту а) знаходимо сторону шестикутника. AC = 2b sin α.
Знайдемо OA – радіус описаного кола: OA = 2b sin α.
З ΔSAO: 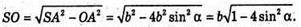
Отже, об’єм V піраміди дорівнює:
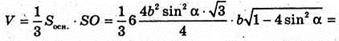
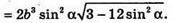
Г) Аналогічно пункту а) знайдемо сторону n-кутника, а = 2b sin α.
Знайдемо R – радіус описаного кола.
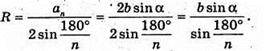
Знайдемо висоту n-кутної піраміди:
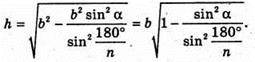
Отже, V піраміди дорівнює:
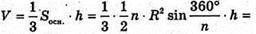
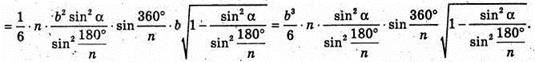
Відповідь: а) 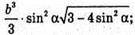 б)
б) 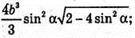 в)
в) 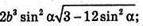
Г) 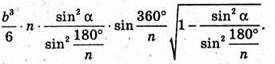
1259.
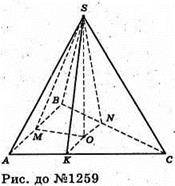
Нехай SABC – задана піраміда, AB = 6 см, BC = 25 см, AC = 29 см.
VSABC = 80 см3, SO + (ABC). Проведемо SK + AC, SN + BC, SM + АВ,
Тоді за теоремою про три перпендикуляри OK + AC, ON + ВС, OM + АВ.
Отже, ∠SNO = ∠SKO = ∠SMO.
Оскільки двогранні кути при основі рівні, то вершина проектується в точу O – центр вписаного кола, OM = OK = ON.
ΔSOM = ΔSOK = ΔSON, отже, SN = SK = SM.
Обчислимо півпериметр основи.
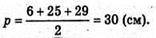
Знайдемо площу основи за формулою Герона:
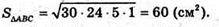
Радіус вписаного кола: 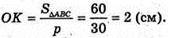
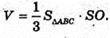
Оскільки V = 80 см 3, то 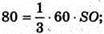
240 = 60SO; SO = 4 (см).
З Δ SON: 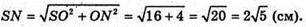
Отже, маємо: 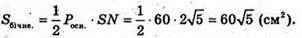
Відповідь: 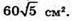
1260.
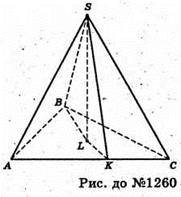
Нехай SABC – задана піраміда, AC = 10 м, SB = 16 м,
SA = SC =AB = BC = 13 м.
З ΔSKC: 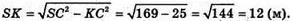
Знайдемо BK з ΔВСК:
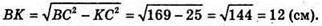
Знайдемо SΔABC за формулою Герона:
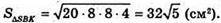
З іншої сторони 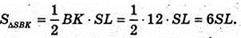
Звідси 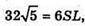
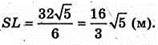
Знайдемо площу трикутника ABC за формулою Герона:
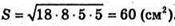
Отже, об’єм піраміди V дорівнює:
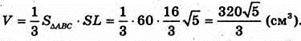
Відповідь: 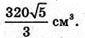
1261.
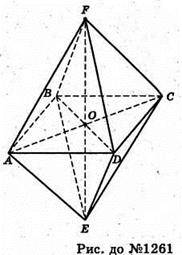
Нехай FABCDE – заданий октаедр.
З ΔABD: 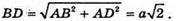
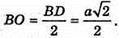
З ΔFOB: 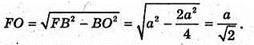
Знайдемо об’єм V піраміди SABCD:
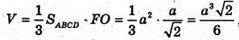
Тоді об’єм V1октаедра:
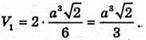
Відповідь: 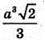
1262.
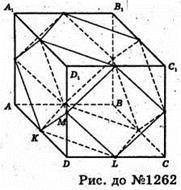
Нехай ABCDA1B1C1D1- куб. Проведемо перерізи через середини кожних трьох ребер куба, які виходять з однієї вершини, отримаємо чотирнадцятигранник; 8 пірамід. Знайдемо об’єм однієї такої піраміди MKDL.
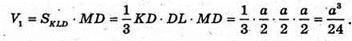
Об’єм 8 пірамід 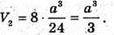
Об’єм куба V = а3.
Отже, об’єм 14-гранника дорівнює: 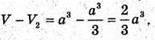
Відповідь: 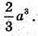
1263.
Нехай S1- площа піраміди, H1 – висота піраміди, S2- площа перерізу, H2- висота від вершини піраміди до перерізу.
Знайдемо об’єм піраміди: V1=S1 × H1.
Знайдемо об’єм піраміди з основою – паралельним перерізом: V2 = S2 × H2.
За властивістю паралельних перерізів піраміди маємо: 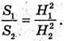
За умовою V1 = V2, отже S1 × H1 = S2 × H2,
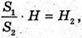
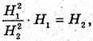 звідси
звідси 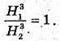
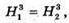
1264.
Нехай вимір мила а, b, с.
З точки зору геометрії мило – це паралелепіпед.
Знайдемо об’єм мила V1 = а, b, с.
Знайдемо об’єм мила через 7 днів.
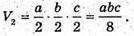
Отже, за 7 днів витрачено мила
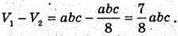
Звідси маємо пропорцію
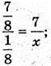
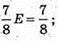 x = 1. Отже, мила залишилося на 1 день.
x = 1. Отже, мила залишилося на 1 день.
Відповідь: 1 день.
1265.
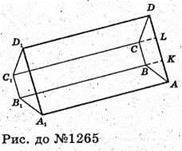
Нехай BC = B1C1 = 12м, CC1 = BB1 = 24м. BK = 4 м, ∠ABC = 120°,
∠KBA = ∠ABC – 90° = 120° – 90° = 30°.
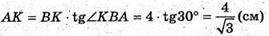
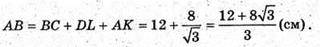
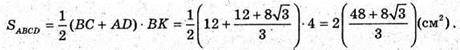
Отже, об’єм котловану дорівнює: V = SABCD × BB1.
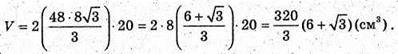
Відповідь: 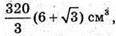 ні.
ні.
1266.
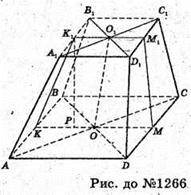
Нехай ABCDA1B1C1D1- зрізана піраміда, AB = BC = CD = DA = 5 см,
A1B1 = B1C1 = C1D1 = D1A1 = 2 см, C1CDD1 + ABCD, ∠K1KO = 45°, ∠M1MO = 90°.
Розглянемо чотирикутник KK1M1M – це прямокутна трапеція.
Проведемо P + KM, тоді отримаємо K1M1 = PM = 2 см,
KP = KM – PM = 5 – 2 = 3 см.
Оскільки ∠K1KO = 45°, то K1P = KP = 3 см.
Отже, об’єм зрізаної піраміди:
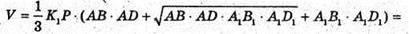
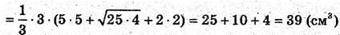
Відповідь: 39 см3.
1267.
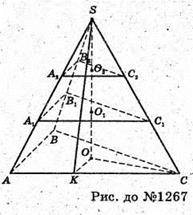
Нехай SABC – задана піраміда SO2 = O2O1 = O1O,
(A2B2C2) ? (ABC), (A1B1C1) ? (ABC), AC = BC = AB = 6 см.
Проведемо SK + AC, тоді за теоремою про три перпендикуляри OK + AC,
Точка O – центр вписаного кола.
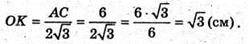
З прямокутного ΔSOK:
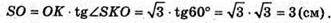
Нехай V – об’єм піраміди SАВС; V2 – об’єм піраміди SA1B1C1; V3- об’єм піраміди SA2B2C2.
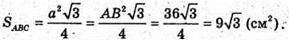
За властивістю паралельних перерізів піраміди маємо:
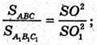
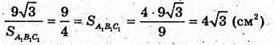
Аналогічно, 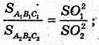
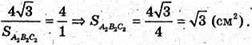
Знайдемо 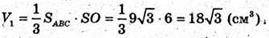
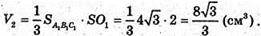
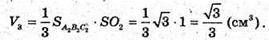
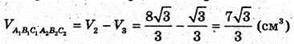
Відповідь: 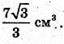
1268.
Нехай H – висота зрізаної піраміди.
Тоді, за властивістю перерізів піраміди, паралельних основі маємо:
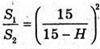 або
або 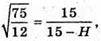
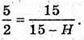 5H = 45 , H = 9.
5H = 45 , H = 9.
Отже, знайдемо об’єм V:
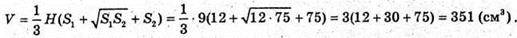
1269.
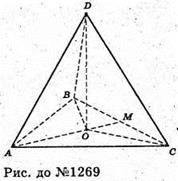
Нехай ABCD – трикутна піраміда, в якій AD = BD = CD = AB = AC = a, BC = b.
Проведемо DO + (ABC), DO – висота, O – центр описаного кола навколо ΔABC (оскільки AD = DB = CD, то і OA = OB = OC).
Нехай R – радіус цього кола, M – середина BC, ∠ABC = α, тоді
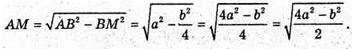
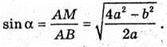
За теоремою синусів: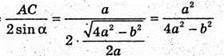
З ΔADO: 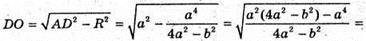
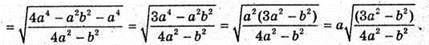
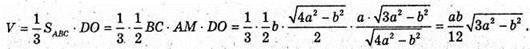
Відповідь: 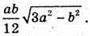
1270.
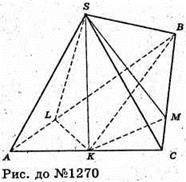
За умовою SABC – піраміда, в якій ABC – рівнобедрений трикутник,
AB = BC, (SAC) + (ABC), ∠ABC = α.
Проведемо SC + AB, SM + BC, SK + AC, тоді за теоремою про три перпендикуляри LK + AB, MK + BC, отже, ∠SLK = ∠SMK = φ, ∠K = 1.
З ΔSLK: SK = LK × tg ∠SLK = l × tgφ.
З ΔLBK: 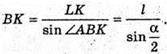
З ΔABK : 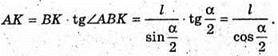
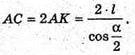
Отже, об’єм піраміди дорівнює:
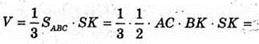
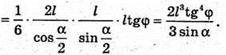
Відповідь: 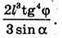
1271.
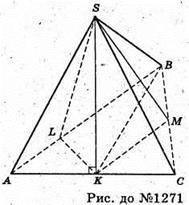
Нехай SABC – задана піраміда, в ΔABC: ∠ABC = 90°, AB = a, ∠BAC = α,
(SAC) + (ABC). Проведемо SL + AB, SM + BC, SK + AC,
Тоді за теоремою про три перпендикуляри LK + AB, MK + BC,
Отже ∠SLK = ∠SMK = 45°.
BK + AC (за теоремою про три перпендикуляри).
З ΔABK : AK = AB × cos ∠BAK = а × cos α.
З ΔALK : LK = AK × sin ∠LAK = a × cos α ×· sin α.
Розглянемо ΔSLK, оскільки ∠SLK = 45°, то і ∠LSK = 45°,
Отже, ΔSLK – рівнобедрений SK = LK = а × cos α × sin α.
З ΔABC: BC = atgα. Отже, об’єм піраміди V дорівнює:
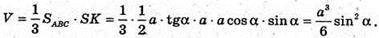
Відповідь: 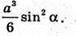
1272.
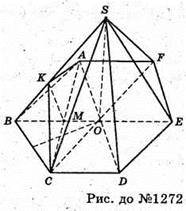
Нехай SABCDEF – задана піраміда із стороною а.
Проведемо AK + SB, CK + SB, тоді ∠AKC = α.
ΔSBO – ΔBKM (оскільки це прямокутні трикутники (∠BKM = ∠SOB = 90°),
∠SBO – спільний). Тоді 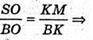
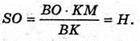
З ΔСКМ: 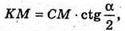 CM = BC cos ∠MCB,
CM = BC cos ∠MCB,
∠MCB = ∠NOC (як кути із взаємно перпендикулярними сторонами).
Отже, ∠MCB = 30° і 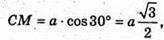
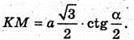
З ΔBKM: 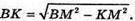
З ΔBMC: 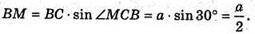
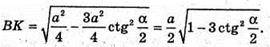
Отже, 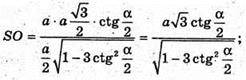
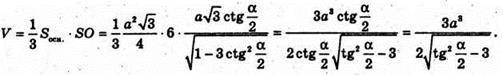
Відповідь: 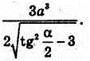
1273.
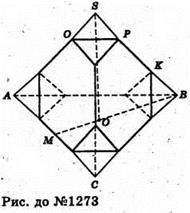
Нехай SABC – заданий тетраедр, AB = BC = AC = SA = SB = SC = а.
SO + (ABC). 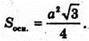
BM – медіана, висота і бісектриса, 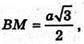
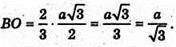
З ΔSOB: 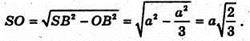
Отже, об’єм тетраедра дорівнює:
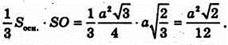
Оскільки утворений многогранник має чотири грані правильні трикутники, а чотири грані правильні шестикутники, то 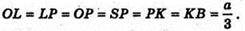
Окрім многогранника, утворилося чотири тетраедра.
Отже, об’єм V1одного з утворених тетраедрів дорівнює:
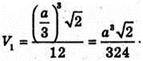
Об’єм V2чотирьох тетраедрів дорівнює:
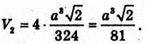
Отже, об’єм многогранника V3 дорівнює:
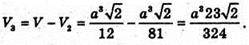
Відповідь: 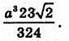
1274.
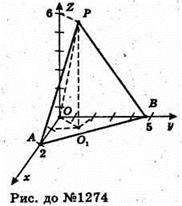
Задано піраміду РАОВ, де O(0; 0; 0), А(2; 0; 0), В(0; 5; 0), Р(1; 2; 6).
Проведемо PO1 + (OAB), тоді PO1 = 6.
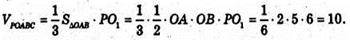
Відповідь: 10.
1275.
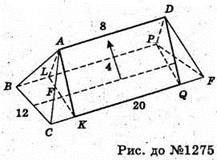
Через точки A і D проведено площини, перпендикулярні площині BEFC.
Тоді отримаємо піраміду, яка складається з двох частин.
ABLCK і DPEFQ і призми AFKPDQ.
Знайдемо об’єм піраміди: 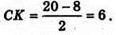
Отже, в основі піраміди лежить квадрат зі стороною 12 см, висота піраміди дорівнює 4 см.
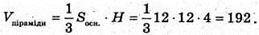
Знайдемо об’єм призми: в основі лежить трикутник зі стороною основи 12 см, висотою 4 см, і висотою призми 8 см.
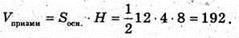
Отже, об’єм горнеда дорівнює
Відповідь: 384.
1276.
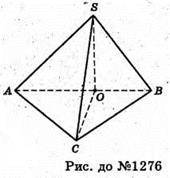
Нехай SA1 = SB = SC = а.
Позначимо висоту SO = H.
З ΔSOB: 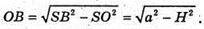
Сторона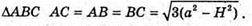
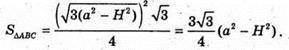
Отже, 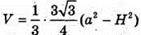
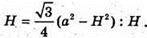
Дослідимо функцію 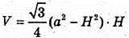
На найбільше значення, якщо H? [0; а].
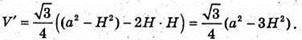
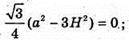 а2 = 3H2;
а2 = 3H2; 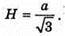
Знайдемо значення V(0), V(а), 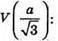
V(0) = 0, V(а) = 0,
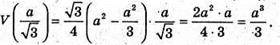
Отже, найбільше значення об’єму даної трикутної піраміди дорівнює
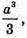 якщо
якщо 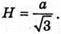
Відповідь: 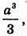 якщо
якщо 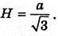
1277.
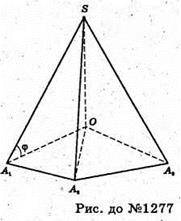
Нехай SA1A2A3… – n-кутна правильна піраміда, SA1 = SA2 = SA3 = … = a,
SO + (A1A2A3).
Нехай ∠SA1O = φ, тоді з ΔSA1O: A1O = SA1cos∠ = acos∠, SO = SA1sin∠ = asin∠.
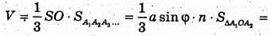
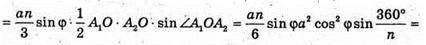
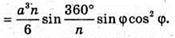
Дослідимо функцію 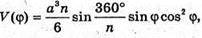
Де φ ? [0; 90°] на найбільше значення:
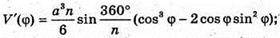
V′(φ) = 0; cos3φ – 2 cos φ × sin2φ = 0; cos φ(cos2φ – 2 sin2φ) = 0;
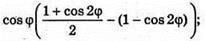
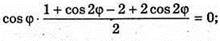
Cos φ(3 cos 2φ – 1) = 0; cos φ = 0 або 3cos 2φ – 1 = 0;
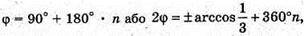
N? Ζ; φ = 90° + 180°n або 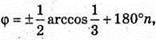 n? Z.
n? Z.
Проміжку [0; 90°] належать лише значення φ = 90° і 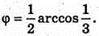
V(0) = 0; V(90°) = 0;
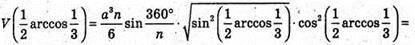

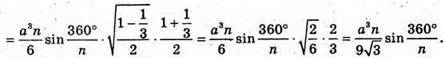
Отже, найбільше значення об’єму – 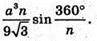
Відповідь: 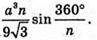
1278.
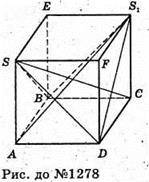
Нехай SABCD, S1ABCD – піраміди, AB = BC = CD = DA = a, SA + (ABCD),
SD1+ (ABCD). Добудуємо наші піраміди до паралелепіпеда, тоді спільна частина двох пірамід буде дорівнювати 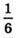 частині паралелепіпеда.
частині паралелепіпеда. 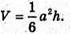
Відповідь: 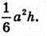
1279.
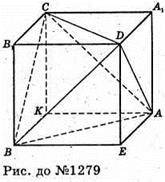
Нехай ABCD – заданий тетраедр, AB = CD = с, AC = BD = b, AD = BC = с.
Добудуємо цей тетраедр до прямокутного паралелепіпеда: через мимобіжні прямі DC і AB, AC і BD, AD і BC проведемо паралельні площини. При взаємному перетині вони утворюють паралелепіпед. Відстань, наприклад, між ребрами тетраедра DC і AB є ребро DE (абоKC). Отже, знайдемо ребра паралелепіпеда х, у, z, якщо діагоналі граней паралелепіпеда дорівнюють а, b, с:
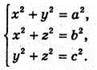
Розв’язавши систему, отримаємо:
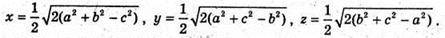
Отже, об’єм
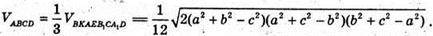
Відповідь: 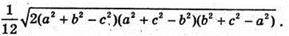
1280.
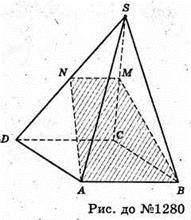
Побудуємо переріз ABMN (MN? AB? CD). Об’єм піраміди SABCDпозначимо V; об’єм піраміди SABMN – V1.
Об’єм піраміди V1дорівнює сумі об’ємів V2 і V3 пірамід SBMN і SBAN.
Порівняємо об’єми пірамід SBMN і SBAN.
Приймемо за основ цих пірамід грані SMN і SCD, точка В – спільна вершина пірамід.
Оскільки 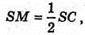 то
то 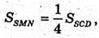 отже,
отже, 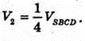
З цього випливає, що 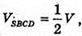 звідси
звідси 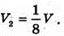
Розглянемо піраміди SBAN і SBAD. За їх основи приймемо грані SAN і SAD, точка В – спільна вершина цих пірамід.
Оскільки N – середина ребра CD, то 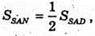 отже,
отже, 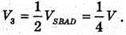
Знайдемо об’єм 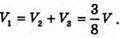
Об’єм другої відсіченої частини дорівнює 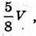 а відношення об’ємів частин дорівнює 3 : 5.
а відношення об’ємів частин дорівнює 3 : 5.
Відповідь: 3 : 5.
1281.
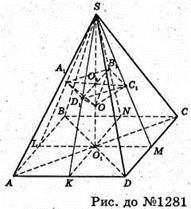
SABCD – правильна піраміда, SO1+ (ABC), O – центр кулі, вписаної в SABCD, OO1 = r, SM +CD, тоді ∠SMO1 = α. A1, B1, C1, D1- точки дотику кулі до бічних граней піраміди: OA1 = OB1 = OC1 = OD1 = г.
D1B1 ? DC, A1C1 ? AD, тоді D1B1 ? A1C1, A1B1 = B1C1 = C1D1 = A1D1.
OA1B1C1D1- правильна піраміда.
Із ΔO1OM: 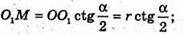
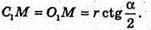
Із ΔSO1M: 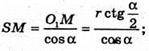
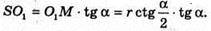
ΔSO2C1- ΔSO1M, тоді 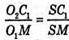 або
або 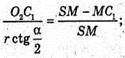
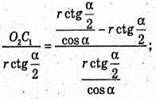
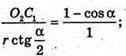
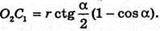
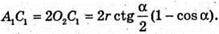
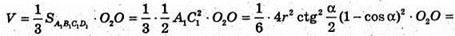
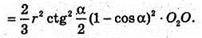
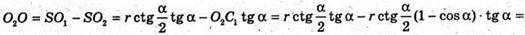
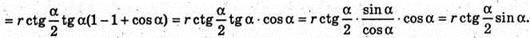
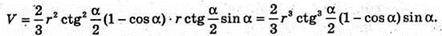
Відповідь: 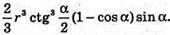
1282.
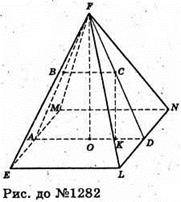
Нехай A i D – середини ребер ME і NL, основи заданої піраміди FEMNL, BC – лінія перетину AFD з даною площиною, дотичною до кулі, вписаної в піраміду, O – проекція вершини F на основу, NL + AD, отже NL + FD (за теоремою про три перпендикуляри), і NL +(AFD), (AFD) + (FNL).
Кут між FO і бічною гранню FNL як раз і є ∠OFD. BC? AD, отже ABCD – рівнобока трапеція, в яку можна вписати коло.
Нехай CK – висота трапеції ABCD, тоді 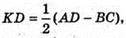
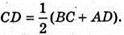

Але 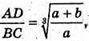 оскільки об’єми подібних пірамід пропорційні кубам відповідних ребер. Отже,
оскільки об’єми подібних пірамід пропорційні кубам відповідних ребер. Отже, 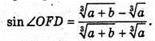
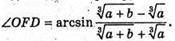
Відповідь: 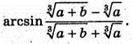
1283.
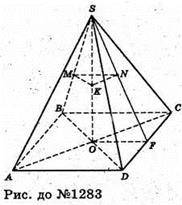
Нехай K – середина висоти SO правильної піраміди SABCD. MK + BS, MK = m, SF + CD, тоді OF + CD, тобто CD + (OFS), (OFS) + (SCD), KN + (SDC), KN = b.
Нехай SO = Н, OF = х, тоді 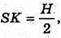
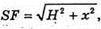
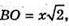
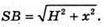
ΔFSO ~ ΔKSN, отже 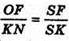 або
або 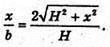
ΔBSO ~ ΔKSM, отже 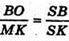 або
або 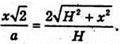
Отримуємо систему:
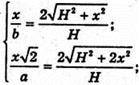
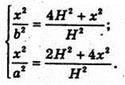
Звідси: 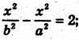
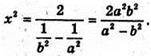
Підставимо в перше рівняння системи, отримаємо:
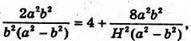 звідси
звідси 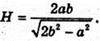
Отже, 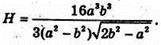
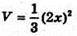
Відповідь: 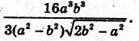
1284.
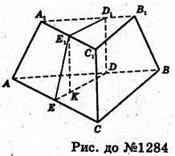
Нехай у зрізаній піраміді ABCA1B1C1 AB = BC = АС = 6см,
A1B1 =B1C1 =A1C1 = 2см. Проведемо EE1+ AC, DE + AC, тоді ∠E1EC1 = 30°.
З ΔADE: 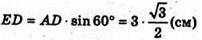
З ΔA1D1E1: 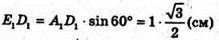
Чотирикутник E1D1DE – прямокутна трапеція.
Проведемо E1K + ED. 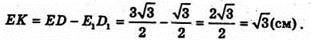
З ΔE1EK: 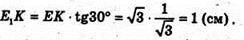
Отже, об’єм зрізаної піраміди V дорівнює:
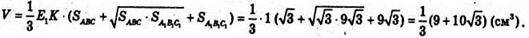
Відповідь: 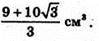
1285.
Нехай ABCA1B1C1- зрізана піраміда, A1B1ML? CC1, O1O = H.
Якщо відповідні сторони основ пропорційні числам 1:3, то площі основ будуть пропорційні числам 1 : 9.
S1- площа ΔA1B1C1, S2- площа 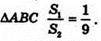
V1- об’єм зрізаного конуса 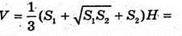
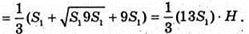
V2- об’єм призми ABCA1B1C1, V3 = S1× H.
V3- об’єм фігури, що залишилася: 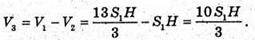
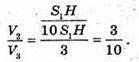
Відповідь: 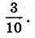
1286.
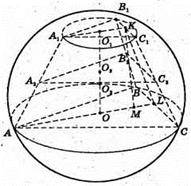
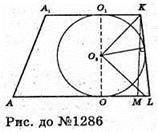
ABCA1B1C1- правильна зрізана піраміда. A2C2- середня лінія трапеції AA1C1C, A2C2 = l. O3O1 = O3O1 де O3- центр кулі, вписаної в зрізану піраміду ABCA1B1C1, тоді O2O3 = d і O2O1 = O3O1 + d, OO2= OO3- d, де O2- центр кулі, описаної навколо зрізаної пірамідиABCA1B1C.
Нехай AB = a, A1B1= b, тоді маємо: 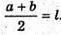 OO1 = 2h.
OO1 = 2h.
Піраміда O2ABC – правильна, тоді
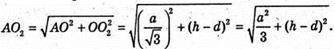
Піраміда O2A1B1C, – правильна, тоді
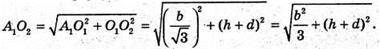
Тоді маємо рівняння AO2 =A1O2або 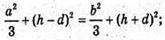
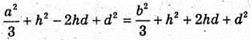 Або
Або 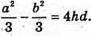
Проведемо AL + BC, A1K + B1C1, KM + (ABC).
Тоді із ΔKLM: KL2 = KM2 + ML2або 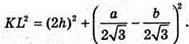
Із ΔO1O3K: 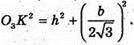
Із ΔOO3L: 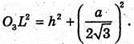
Враховуючи, що ΔO3KL – прямокутний, маємо:
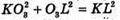 Або
Або 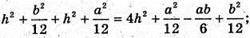
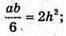 ab = 12h2.
ab = 12h2.
Отже, маємо систему:
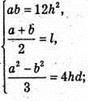
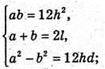
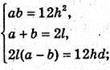
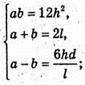
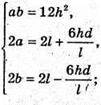
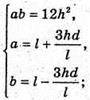
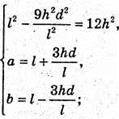
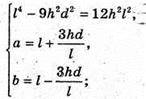
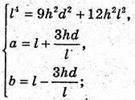
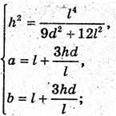
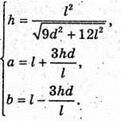
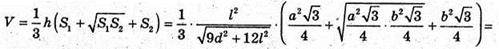
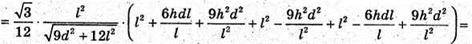
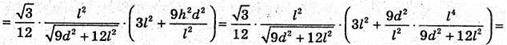
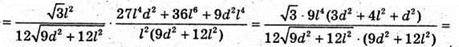
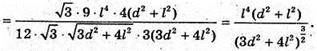
Відповідь: