Головна ⇒ 📌Довідник з математики ⇒ Основна властивість дробу. Скорочення дробів – Раціональні вирази
Основна властивість дробу. Скорочення дробів – Раціональні вирази
Математика – Алгебра
Раціональні вирази
Основна властивість дробу. Скорочення дробів
Якщо чисельник і знаменник дробу помножити або поділити на один і той самий вираз, то дістанемо дріб, який тотожно дорівнює даному. Це дозволяє скорочувати дроби й приводити їх до нового знаменника.
Приклади
1) 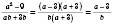 .
.
Зверніть увагу: щоб скоротити дріб, його чисельник і знаменник треба розкласти на множники.
2) Зведіть дріб 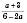 до знаменника
до знаменника 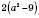 .
.
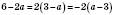 ,
,
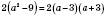 .
.
Із цього видно, що додатковий множник дорівнює 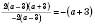 .
.
Отже, маємо:
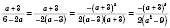 .
.
Зверніть увагу на тотожності:
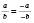 ;
; 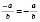 ;
; 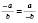 .
.
Related posts:
- Основна властивість дробу – Додавання і віднімання звичайних дробів Математика – Алгебра Додавання і віднімання звичайних дробів Основна властивість дробу Якщо чисельник і знаменник дробу помножити або поділити на одне й те саме натуральне число, дістанемо дріб, що дорівнює даному. Рівні дроби – це різні записи одного й того ж числа. Застосування основної властивості дробу Скорочення дробу Ділення чисельника і знаменника дробу на їхній […]...
- Множення, ділення й піднесення до степеня дробів – Раціональні вирази Математика – Алгебра Раціональні вирази Множення, ділення й піднесення до степеня дробів Щоб помножити дріб на дріб, треба перемножити окремо їхні чисельники й окремо знаменники і перший добуток записати чисельником, а другий – знаменником дробу. Щоб піднести дріб до степеня, треба піднести до цього степеня чисельник та знаменник і перший результат записати чисельником, а другий […]...
- Основна властивість дробу. Скорочення дробів Урок № 3 Тема. Основна властивість дробу. Скорочення дробів Мета: домогтися засвоєння учнями змісту основної властивості раціонального дробу, понять скорочення дробу та правила знаків; сформувати вміння відтворювати зміст названих понять та використовувати вивчені поняття для розв’язування вправ на скорочення раціональних дробів та перетворення їх за допомогою правила знаків. Тип уроку: засвоєння знань та вмінь. Наочність […]...
- ОСНОВНА ВЛАСТИВІСТЬ ДРОБУ. СКОРОЧЕННЯ ДРОБУ Розділ 2 ЗВИЧАЙНІ ДРОБИ ТА ДІЇ З НИМИ У розділі дізнаєтесь: Ü про основну власти віст в дробу; Ü як скорочувати дроби; Ü як зводити дроби до спільного знаменника; Ü як порівнювати дроби з різними знаменниками; Ü як виконувати арифметичні дії з дробами; Ü що таке десяткові наближення звичайного дробу; Ü як застосувати вивчений матеріал […]...
- Раціональні вирази. Основна властивість дробу. Додавання і віднімання дробів Урок № 11 Тема. Раціональні вирази. Основна властивість дробу. Додавання і віднімання дробів Мета: перевірити рівень знань та вмінь учнів, набутих ними піл час вивчення теми “Раціональні вирази”. Тип уроку: контроль знань та вмінь. Хід уроку I. Організаційний етап II. Перевірка домашнього завдання Зібрати зошити з виконаною домашньою контрольною роботою № 1 (роботу перевірити та […]...
- Основна властивість дробу. Зведення дробів до нового знаменника Урок № 4 Тема. Основна властивість дробу. Зведення дробів до нового знаменника Мета: домогтися засвоєння учнями змісту основної властивості раціонального дробу (у двох варіантах) та схеми її доведення, змісту поняття “скоротити раціональний дріб” та алгоритму скорочення раціонального дробу, а також правила знаків для раціональних дробів; сформувати вміння відтворювати названі властивості й використовувати ці властивості та […]...
- Додавання та віднімання дробів – Раціональні вирази Математика – Алгебра Раціональні вирази Додавання та віднімання дробів 1. Щоб додати (відняти) дроби з однаковими знаменниками, треба додати (відняти) їхні чисельники, а знаменник залишити той самий. Наприклад: 1) . 2) . 2. Якщо треба знайти суму або різницю дробів з різними знаменниками, то спочатку дроби зводять до спільного знаменника. Приклади 1) ; спільний знаменник […]...
- Перетворення звичайних дробів на десяткові – Додавання і віднімання звичайних дробів Математика – Алгебра Додавання і віднімання звичайних дробів Перетворення звичайних дробів на десяткові Щоб перетворити звичайний дріб на десятковий, треба ділити чисельник на знаменник за правилом ділення десяткових дробів. У деяких випадках отримаємо скінченний десятковий дріб. Приклад . В інших випадках дістанемо нескінченний періодичний десятковий дріб, тобто такий, у записі якого одна чи декілька цифр […]...
- Повторення відомостей про звичайні дроби. Основна властивість дробу Урок № 11 Тема. Повторення відомостей про звичайні дроби. Основна властивість дробу Мета: повторити відомості про звичайні дроби, набуті в 5 класі (зміст чисельника і знаменника звичайного дробу, запис, читання; дріб як частка; порівняння [додавання і віднімання дробів з однаковими знаменниками], види дробів: правильний і неправильний; запис неправильного дробу і мішане число і т. ін.); […]...
- Задачі і рівняння на додавання і віднімання дробів. Порівняння дробів. Основна властивість дробу Урок № 22 Тема. Задачі і рівняння на додавання і віднімання дробів. Порівняння дробів. Основна властивість дробу Мета: підготовити учнів до виконання тематичної контрольної роботи. Тип уроку: узагальнення та систематизації знань. Хід уроку I. Перевірка домашнього завдання @Урок є підсумковим з теми “Порівняння, додавання і віднімання дробових чисел”, тому вчитель, враховуючи особливості кожного класу, звертає […]...
- Найменший спільний знаменник дробів. Зведення дробів до спільного знаменника. Порівняння дробів Розділ 2 Звичайні дроби §9. Найменший спільний знаменник дробів. Зведення дробів до спільного знаменника. Порівняння дробів Ми вже вміємо порівнювати дроби з однаковими знаменниками: з двох дробів з однаковими знаменниками більшим є той, у якого більший чисельник. Наприклад, А як порівнювати дроби з різними знаменниками? Приклад 1. Порівняти дроби Розв’язання. Використаємо основну властивість дробу і […]...
- Зведення дробів до спільного знаменника – Додавання і віднімання звичайних дробів Математика – Алгебра Додавання і віднімання звичайних дробів Зведення дробів до спільного знаменника Будь-які дроби можна звести до спільного знаменника. Таким знаменником може бути будь-яке спільне кратне знаменників цих дробів. Зрозуміло, що звичайно обирають найменший спільний кратний знаменник (НСЗ). Щоб звести дроби до найменшого спільного знаменника, треба: 1) знайти найменше спільне кратне знаменників; 2) знайти […]...
- Порівняння звичайних дробів Математика – Алгебра Звичайні дроби Порівняння звичайних дробів Із двох дробів з однаковими знаменниками більший той, чисельник якого більший. Із двох дробів з однаковими чисельниками менший той, знаменник якого більший. Правильний дріб менший за одиницю. Дріб, у якого чисельник дорівнює знаменнику, дорівнює одиниці. Дріб, у якого чисельник більший від знаменника, більший від одиниці. Неправильний дріб […]...
- Множення звичайних дробів Математика – Алгебра Множення і ділення звичайних дробів Множення звичайних дробів Добутком звичайних дробів є дріб, чисельник якого дорівнює добутку чисельників цих дробів, а знаменник дорівнює добутку їхніх знаменників. (Отриманий дріб, як правило, скорочують.) Наприклад: . Щоб помножити дріб на натуральне число, його чисельник помножують на це число, а знаменник залишають без зміни. Наприклад: ; […]...
- Дроби. Дробові вирази. Раціональні вирази. Допустимі значення змінних Урок № 2 Тема. Дроби. Дробові вирази. Раціональні вирази. Допустимі значення змінних Мета: домогтися засвоєння учнями термінології, вивченої на попередньому уроці, та засвоєння змісту алгоритму знаходження значень змінної, при яких даний раціональний дріб дорівнює нулю; сформувати вміння застосовувати вивчений алгоритм для розв’язування вправ, що передбачають знаходження значень змінних, при яких значення поданого раціонального дробу дорівнює […]...
- ЗВЕДЕННЯ ДРОБІВ ДО СПІЛЬНОГО ЗНАМЕННИКА. ПОРІВНЯННЯ ДРОБІВ Розділ 2 ЗВИЧАЙНІ ДРОБИ ТА ДІЇ З НИМИ § 7. ЗВЕДЕННЯ ДРОБІВ ДО СПІЛЬНОГО ЗНАМЕННИКА. ПОРІВНЯННЯ ДРОБІВ Ви вже знаєте, що дріб можна замінити дробом тому, що значення цих дробів рівні: Про таку рівність кажуть, що дріб звели до нового знаменника 16. Під час зведення дробу до нового знаменника застосовують основну властивість дробу. Часто наперед […]...
- Звичайні дроби Математика – Алгебра Звичайні дроби Записи виду називаються звичайними дробами, або дробами. Звичайні дроби записують за допомогою двох натуральних чисел та горизонтальної риски, яка називається дробовою рискою. Число, записане під рискою, називається знаменником дробу, а число, записане над рискою, – чисельником. Знаменник показує, на скільки рівних частин поділено одиницю (ціле), а чисельник – скільки таких […]...
- Скорочення звичайних дробів Урок № 13 Тема. Скорочення звичайних дробів Мета: закріпити знання учнів про скорочення дробів та спосіб застосування цих знань для розв’язування вправ на скорочення дробів; вдосконалювати вміння учнів виконувати скорочення дробів у комплексі з іншими, вивченими раніше перетвореннями звичайних дробів. Тип уроку: застосування знань, навичок, умінь. Хід уроку І. Перевірка домашнього завдання. Актуалізація опорних знань […]...
- Перетворення звичайного дробу в десятковий і навпаки Математика – Алгебра Порівняння та округлення натуральних чисел і десяткових дробів Перетворення звичайного дробу в десятковий і навпаки Будь-який десятковий дріб можна записати як звичайний із знаменником виду 10, 100, 1000 і так далі: ; ; . Щоб перетворити звичайний дріб на десятковий, треба чисельник поділити на знаменник за правилом ділення десяткових дробів. Інколи таке […]...
- Властивості десяткового дробу – Десяткові дроби Математика – Алгебра Десяткові дроби Властивості десяткового дробу Якщо до десяткового дробу дописати справа нуль (або декілька нулів), то дістанемо дріб, який дорівнює даному. Якщо десятковий дріб закінчується нулями, то ці нулі можна відкинути й дістанемо дріб, який дорівнює даному. Наприклад: ; ....
- Порівняння, додавання та віднімання дробів – Додавання і віднімання звичайних дробів Математика – Алгебра Додавання і віднімання звичайних дробів Порівняння, додавання та віднімання дробів Щоб виконати порівняння, додавання, віднімання дробів із різними знаменниками, треба звести їх до найменшого спільного знаменника, а потім виконати потрібну дію за аналогічним правилом для дробів з однаковими знаменниками. Завжди треба звертати увагу, чи можна спростити отримане число: виділити цілу частину або […]...
- Спільний знаменник кількох дробів. Зведення звичайних дробів до найменшого спільного знаменника Урок № 14 Тема. Спільний знаменник кількох дробів. Зведення звичайних дробів до найменшого спільного знаменника Мета: на основі основної властивості дробу сформувати уявлення учнів про зміст поняття зведення дробів до спільного знаменника, а також розпочати роботу з вироблення вмінь зводити дроби до найменшого спільного знаменника. Тип уроку: засвоєння нових знань. Хід уроку І. Перевірка домашнього […]...
- Ділення звичайних дробів Математика – Алгебра Множення і ділення звичайних дробів Ділення звичайних дробів Щоб поділити один дріб на інший, досить ділене помножити на число, обернене дільнику. Приклади 1) ; 2) ; 3) ; 4) . Знаходження дробу від числа і числа за даним значенням його дробу Щоб знайти дріб від числа, треба число помножити на цей дріб. […]...
- ДРОБИ. ЧИСЕЛЬНИК, ЗНАМЕННИК ДРОБУ ДРОБИ ДРОБИ. ЧИСЕЛЬНИК, ЗНАМЕННИК ДРОБУ 1020. Розглянь схеми. 1) Як можна отримати третину відрізка? Третину від цілого? 2) Скільки третин у цілому? Скільки половин, четвертин, восьмих у цілому? 3) У скільки разів ціле більше від половини? Від третини? Від десятини? 4) У скільки разів половина менша від цілого? Четверта частина менша від цілого? 1021. Паперова […]...
- Перетворення раціональних виразів – Раціональні вирази Математика – Алгебра Раціональні вирази Перетворення раціональних виразів Будь-який раціональний вираз можна подати у вигляді дробу або цілого виразу. Це можна зробити на основі правил дій над дробами та цілими виразами. Треба розуміти, що для раціональних виразів мають місце відомі властивості дій (переставна та сполучна властивість додавання і множення та ін.). Запис можна вести у […]...
- ДОПОВНЕННЯ ПРАВИЛЬНОГО ДРОБУ ДО ОДИНИЦІ. ВІДНІМАННЯ ДРОБУ ВІД НАТУРАЛЬНОГО ЧИСЛА РОЗДІЛ 6 ДІЇ ПЕРШОГО СТУПЕНЯ ЗІ ЗВИЧАЙНИМИ ДРОБАМИ З ОДНАКОВИМИ ЗНАМЕННИКАМИ § 27. ДОПОВНЕННЯ ПРАВИЛЬНОГО ДРОБУ ДО ОДИНИЦІ. ВІДНІМАННЯ ДРОБУ ВІД НАТУРАЛЬНОГО ЧИСЛА Мал. 216 Подивіться на малюнок 216. Ви бачите, що п’ятикутник поділено на 5 рівних трикутників. Два з них зафарбовано, а три – ні. Зрозуміло, що зафарбовані і незафарбована частини п’ятикутника доповнюють одна […]...
- МНОЖЕННЯ ДРОБІВ. ЗНАХОДЖЕННЯ ДРОБУ ВІД ЧИСЛА Розділ 2 ЗВИЧАЙНІ ДРОБИ ТА ДІЇ З НИМИ § 9. МНОЖЕННЯ ДРОБІВ. ЗНАХОДЖЕННЯ ДРОБУ ВІД ЧИСЛА Дроби, як і натуральні числа, можна множити. Наприклад, щоб знайти площу прямокутника зі сторонами 3 см і 4 см, треба помножити ці числа: 3 ∙ 4 = 12 (см2). Але Тому, у квадратних дециметрах площа даного прямокутника дорівнює добутку […]...
- ПЕРЕТВОРЕННЯ ЗВИЧАЙНОГО ДРОБУ В ДЕСЯТКОВИЙ. ДЕСЯТКОВІ НАБЛИЖЕННЯ ЗВИЧАЙНОГО ДРОБУ Розділ 2 ЗВИЧАЙНІ ДРОБИ ТА ДІЇ З НИМИ §11. ПЕРЕТВОРЕННЯ ЗВИЧАЙНОГО ДРОБУ В ДЕСЯТКОВИЙ. ДЕСЯТКОВІ НАБЛИЖЕННЯ ЗВИЧАЙНОГО ДРОБУ Із курсу математики 5 класу ви знаете, що будь-який десятковий дріб можна записати у вигляді звичайного дробу. Наприклад, Таку дію інакше називають перетворенням десяткового дробу в звичайний. Обернену дію називають перетворенням звичайного дробу в десятковий. Нехай дроби […]...
- Пропорція. Основна властивість пропорції Розділ 3 Відношення і пропорції §21. Пропорція. Основна властивість пропорції Відношення 12 : 3 і 20 : 5 рівні, оскільки їх значення дорівнюють 4. Тому можна записати рівність Рівність двох відношень називають пропорцією. Слово “пропорція” походить від латинського proportio, що означає “співрозмірність”, тобто певне відношення частин між собою. За допомогою букв пропорцію записують так: Ці […]...
- Додавання і віднімання дробів з однаковими знаменниками Математика – Алгебра Звичайні дроби Додавання і віднімання дробів з однаковими знаменниками Щоб додати дроби з однаковими знаменниками, треба додати їх чисельники і суму записати в чисельнику, а знаменник залишити той самий: . Щоб відняти дроби з однаковими знаменниками, треба від чисельника зменшуваного відняти чисельник від’ємника й різницю записати в чисельнику, а знаменник залишити той […]...