Головна ⇒ 📌Довідник з математики ⇒ Основні теореми про границі числової послідовності
Основні теореми про границі числової послідовності
Математика – Алгебра
Границя
Основні теореми про границі числової послідовності
Теорема 1. Нехай послідовності 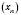 і
і 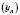 мають відповідно границі a і b. Тоді послідовність
мають відповідно границі a і b. Тоді послідовність 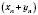 має границю
має границю 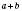 .
.
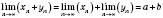 .
.
Теорема 2. Нехай послідовності 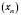 і
і 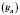 мають відповідно границі a і b. Тоді послідовність
мають відповідно границі a і b. Тоді послідовність 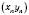 має границю, яка дорівнює ab:
має границю, яка дорівнює ab:
Наслідки
1) Сталий множник можна виносити за знак границі. Якщо С – сonst і
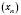 має границю, то
має границю, то 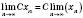 .
.2) Якщо
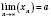 , а k – натуральне число, то
, а k – натуральне число, то 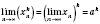 .
.Теорема 3. Нехай послідовності
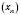 і
і 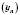 мають скінченні границі, які відповідно дорівнюють
мають скінченні границі, які відповідно дорівнюють 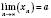 ,
, 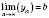 , причому
, причому 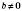 . Тоді послідовність
. Тоді послідовність 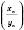 має скінченну границю, яка дорівнює
має скінченну границю, яка дорівнює 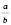
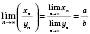 .
.Послідовність називається Неспадною (незростаючою), якщо для будь-якого n Є N виконується нерівність
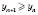
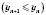 .
.Неспадні та незростаючі послідовності називають Монотонними.
Якщо значення членів монотонної послідовності
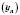 для будь-якого n Є N задовольняють строгу нерівність
для будь-якого n Є N задовольняють строгу нерівність 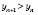
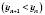 , то послідовність
, то послідовність 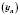 називають Зростаючою (спадною). Зростаючі та спадні послідовності називають також Строго монотонними.
називають Зростаючою (спадною). Зростаючі та спадні послідовності називають також Строго монотонними.Теорема 4 (Вейєрштрасса). Зростаюча або спадна обмежена послідовність має границю.
Теорема 5. Якщо послідовність
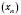 має границю, то ця границя єдина.
має границю, то ця границя єдина.Приклади границь послідовностей
1)
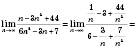
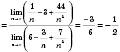 .
.2)

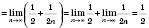 .
.Зверніть увагу на таку границю:
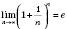 .
.Число е є основою натурального логарифма. Позначення:
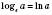 . Число е є ірраціональним, його наближене значення
. Число е є ірраціональним, його наближене значення 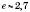 .
.Показникова функція з основою е
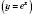 називається Експонентою.
називається Експонентою.Related posts:
- Основні теореми про границі функцій Математика – Алгебра Границя Основні теореми про границі функцій Теорема 1. Якщо функції і в точці мають границі, то сума і добуток цих функцій також мають у цій точці границю, причому ; . Теорема 2. Якщо функції і в точці мають границі й , то й функція має в цій точці границю, яка дорівнює . […]...
- Границя числової послідовності Математика – Алгебра Границя Границя числової послідовності Число a називається Границею послідовності,, …, , …, якщо для будь-якого додатного числа існує таке натуральне число , що для всіх виконується нерівність . Позначеня: , або . Послідовність , , 2, … називається Нескінченно малою, якщо для будь-якого додатного числа ε існує натуральне число N таке, що […]...
- Послідовності Математика – Алгебра Послідовності Розглянемо яку-небудь множину, що містить дійсних чисел і кожний елемент якої відповідає одному з натуральних чисел від 1 до , або нескінченну множину дійсних чисел, кожному елементу якої можна поставити у відповідність натуральне число. Такі числа можна записати в певному порядку. Кажуть, що вони утворюють Послідовність. Наприклад: 2; 4; 6; 8; […]...
- Властивості нескінченно малих послідовностей Математика – Алгебра Границя Властивості нескінченно малих послідовностей Теорема 1. Алгебраїчна сума скінченного числа нескінченно малих послідовностей є нескінченно малою послідовністю. Послідовність називається Обмеженою, якщо існує таке число , що для всіх значень 2, … виконується нерівність . Теорема 2. Добуток нескінченно малої числової послідовності та обмеженої послідовності є нескінченно малою послідовністю. Послідовність називається Нескінченно […]...
- Числові послідовності УРОК № 65 Тема. Числові послідовності Тестові завдання 1. Послідовність задано формулою аn = 5n + 2. Знайдіть а3. А) 3; б) 17; в) 5; г) інша відповідь. 2. В арифметичній прогресії (bп) різниця дорівнює 2. Знайдіть b10, якщо b1 = 3. А) 1536; б) 18; в) 21; г) інша відповідь. 3. Знайдіть суму перших […]...
- Числові послідовності. Властивості числових послідовностей УРОК № 49 Тема. Числові послідовності. Властивості числових послідовностей Мета уроку: домогтися засвоєння учнями змісту понять: числова послідовність, n-й член числової послідовності, формула п-го члена; списку способів задання числової послідовності. Виробити вміння: відтворювати вивчені означення; знаходити члени послідовності із заданими номерами, якщо послідовності задані різними способами. Повторити означення числової функції, а також супутні поняття. Тип […]...
- Границя функції Математика – Алгебра Границя Границя функції Нехай функція визначена на проміжку (можливо, що ). Число A називається границею функції у точці , якщо для будь-якого числа існує таке число , що для всіх , і таких, що , виконується нерівність . Позначення: , або . Нехай – внутрішня точка проміжку . Функція називається нескінченно малою […]...
- Арифметична прогресія Математика – Алгебра Послідовності Арифметична прогресія Арифметичною прогресією називається послідовність, кожний член якої, починаючи з другого, дорівнює попередньому члену, до якого додають одне й те саме число. Це стале для даної послідовності число d називається Різницею арифметичної прогресії. Арифметична прогресія буде зростаючою, якщо , і спадною, якщо . Прогресію можна задати за допомогою першого члена […]...
- Теореми § 2. Трикутники 11. Теореми 269. Теорема Умова Висновок 4.1 Кути АОС і СОВ – суміжні ∠AOC + ∠COB = 180° 8.2 X належить серединному перпендикуляру відрізка AB ХА = ХВ 9.1 ?ABC – рівнобедрений з основою АС 1) ∠A = ∠C; 2) бісектриса кута В є медіаною і висотою 10.3 Два кути трикутника ABC […]...
- Пряма й обернена теореми Геометрія Основні властивості найпростіших геометричних фігур Пряма й обернена теореми Формулювання теореми складається з двох частин. В одній говориться про те, що дано. Ця частина називається Умовою. У другій частині говориться про те, що треба довести. Ця частина називається Висновком. Приклади 1) Якщо кути суміжні, то їх сума дорівнює 180°. Умова Висновок 2) У прямокутному […]...
- Основні властивості неперервних функцій Математика – Алгебра Границя Основні властивості неперервних функцій Теорема 1. Якщо функції і є неперервними в точці , то в цій точці будуть неперервними і функції , . Теорема 2. Якщо і є неперервними в точці і , то в точці є неперервною також і функція . Зверніть увагу: всі дробово-раціональні функції і основні тригонометричні […]...
- ЗАКОН ПОСЛІДОВНОСТІ ПРОХОДЖЕННЯ ФАЗ РОЗВИТКУ Екологія – охорона природи ЗАКОН ПОСЛІДОВНОСТІ ПРОХОДЖЕННЯ ФАЗ РОЗВИТКУ – фази розвитку прир. системи можуть проходити лише в еволюційно закріпленому порядку (історично, екологічно зумовленому), від відносно простого до складного, як правило, без випадання проміжних етапів (однак, можливо, з дуже швидким їх проходженням або еволюційно закріпленою відсутністю). Напр., метаморфоз комах з повним перетворенням може відбуватися лише […]...
- Арифметичні операції над диференційовними функціями Математика – Алгебра Похідна Арифметичні операції над диференційовними функціями Теорема 1. Якщо функції і в точці мають похідні, то функція в цій точці також має похідну, яка дорівнює . Теорема 2. Якщо функції і в точці мають похідні, то в цій точці функція також має похідну, яка дорівнює . Наслідок. Якщо функція має похідну в […]...
- Геометрична прогресія Математика – Алгебра Послідовності Геометрична прогресія Геометричною прогресією називається послідовність відмінних від 0 чисел, кожний член якої, починаючи з другого, дорівнює попередньому члену, помноженому на одне й те саме число. Це стале для даної послідовності число q називають Знаменником геометричної прогресії. Формула n-го члена геометричної прогресії: . Теорема. Послідовність тоді й тільки тоді є геометричною […]...
- Наслідки теореми косинусів УРОК № 5 Тема. Наслідки теореми косинусів Мета уроку: виведення наслідків із теореми косинусів. Формування вмінь учнів застосовувати теорему косинусів і наслідків з неї до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Співвідношення між сторонами і кутами трикутника” [13]. Вимоги до рівня підготовки учнів: застосовують теорему косинусів до розв’язування задач. Хід уроку І. […]...
- Практична робота “Визначення технологічної послідовності виготовлення виробу з аплікацією” Розділ 2. ОЗДОБЛЕННЯ ВИРОБІВ АПЛІКАЦІЄЮ Урок № 7 Тема. ПОСЛІДОВНІСТЬ ВИГОТОВЛЕННЯ ВИРОБУ З АПЛІКАЦІЄЮ Практична робота “Визначення технологічної послідовності виготовлення виробу з аплікацією” Мета уроку: Навчальна: забезпечити засвоєння учнями знань про технологічну послідовність виготовлення будь-якого виробу, формувати вміння планувати й виконувати технологічні операції; Розвивальна: розвивати логічне мислення, уміння аналізувати та співставляти; Виховна: виховувати потребу проявити […]...
- Основні властивості кубічного кореня – СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Формули й таблиці МАТЕМАТИКА СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Основні властивості кубічного кореня Для будь-яких дійсних чисел a й b: 1) а = ()3; 2) = а; 3) = ; 4) якщо b ≠ 0, то ; 5) = тільки тоді, коли а = b; 6) < тільки тоді, коли а < b; 7) < тільки тоді, […]...
- Зміни послідовності нуклеотидів ДНК МЕДИЧНА БІОЛОГІЯ Розділ 1 БІОЛОГІЧНІ ОСНОВИ ЖИТТЄДІЯЛЬНОСТІ ЛЮДИНИ 1.2. Молекулярно-генетичний і клітинний рівні організації життя 1.2.3. Спадковий апарат еукаріотичних клітин і його функціонування на молекулярному рівні 1.2.3.15. Зміни послідовності Нуклеотидів ДНК Мутації гена здебільшого є наслідком зміни послідовності нуклеотидів ДНК. Структурна класифікація мутацій гена: 1) заміна одних азотних основ іншими (транспозиція); 2) зміна кількості нуклеотидних […]...
- ТЕОРЕМИ І АКСІОМИ РОЗДІЛ 2 ВЗАЄМНЕ РОЗТАШУВАННЯ ПРЯМИХ НА ПЛОЩИНІ & 8. ТЕОРЕМИ І АКСІОМИ Ви вже маєте уявлення про теореми. Теорема – це твердження, в істинності якого переконуються за допомогою логічних міркувань, доведень. Звичайно теорема містить умову (те, що дано) і висновок (що вимагається довести). Щоб виокремити умову і висновок теореми, її зручно подати у формі “Якщо…, […]...
- Практична робота 1. Координати комірок. Діапазон комірок. Введення й редагування числової, формульної та текстової інформації ТЕМА 5.4. ЕЛЕКТРОННІ ТАБЛИЦІ (10 ГОДИН) Урок 50 Практична робота 1. Координати комірок. Діапазон комірок. Введення й редагування числової, формульної та текстової інформації Мета: – формувати навички вводу числової, формульної та текстової інформації за допомогою програми опрацювання електронних таблиць; – повторити і закріпити засвоєні на попередньому уроці уміння та навичок щодо використання основних понять ЕТ; […]...
- Теореми про рівність і подібність трикутників – ТРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ТРИКУТНИКИ Трикутник – де багатокутник із трьома сторонами. Сторони трикутника позначаються малими буквами, що відповідають позначенню протилежних вершин. Якщо всі три кути гострі – трикутник гострокутний. Якщо один з кутів прямий – прямокутний; сторони, що утворюють прямий кут, називаються катетами (а і b), сторона проти прямого кута – гіпотенузою (с). Якщо […]...
- Теорема, обернена до теореми Піфагора Урок № 35 Тема. Теорема, обернена до теореми Піфагора Мета: домогтися свідомого розуміння учнями змісту теореми Піфагора та її доведення: сформувати поняття єгипетського трикутника, піфагорової трійки чисел, піфагорових трикутників. Формувати вміння відтворювати зміст вивченої теореми та застосовувати її під час розв’язування задач на доведення. Тип уроку: засвоєння нових знань. Наочність та обладнання: конспект “Теорема Піфагора”. […]...
- Множення вектора на число Геометрія Вектори Множення вектора на число Добутком вектораНа число називається вектор , тобто . Для будь-якого вектора і чисел і . Для будь-яких двох векторів і і числа . Теорема 1. Абсолютна величина вектора дорівнює . Напрям вектора , якщо , збігається з напрямом вектора , якщо , і протилежний напряму вектора , якщо . […]...
- Розв’язування задач на застосування теореми синусів УРОК № 8 Тема. Розв’язування задач на застосування теореми синусів Мета уроку: формування вмінь учнів застосовувати теорему синусів до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Співвідношення між сторонами і кутами трикутника” [13], посібник [14]. Вимоги до рівня підготовки учнів: застосовують теорему синусів до розв’язування задач. Хід уроку І. Перевірка домашнього завдання 1. […]...
- ОСНОВНІ ВЛАСТИВОСТІ ЛОГАРИФМІВ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ВЛАСТИВОСТІ ЛОГАРИФМІВ Для будь-якого додатного числа а, що не дорівнює 1: 1) loga1 = 0; 2) logaa = 1; 3) якщо х > 0 і у > 0, то logaху = logaх + logaу; 4) якщо х > 0 і у > 0, то logax/y = logax – logaу; 5) […]...
- Нерівності Математика – Алгебра Нерівності Число а вважається більшим від b, якщо різниця – число додатне. Число a менше від b, якщо різниця – число від’ємне. Якщо , то числа a і b рівні. На координатній прямій меншому числу відповідає точка, що лежить ліворуч від точки, яка відповідає більшому числу. Позначення: – a менше від b; […]...
- Основні властивості рівнянь Математика – Алгебра Рівняння Два рівняння називають Рівносильними, якщо вони мають одні й ті ж корені; рівняння, які не мають коренів, також вважають рівносильними. Основні властивості рівнянь 1. Якщо виконати тотожні перетворення деякої частини рівняння, то одержимо рівняння, рівносильне даному. 2. Якщо деякий доданок перенести з однієї частини рівняння в іншу, змінивши при цьому його […]...
- Що таке функція 783. 1) так; 2) ні; 3) ні. 784. 1) так; 2) ні; 3) ні. 785. у = 2x + 3. Область визначення (D(f)): будь-яке значення аргумента; Область значень (Е(f)): будь-яке значення функції. 786. у = х+1 X 1 -1 2 У 2 0 3 D(f) = D(y): -1; 1; 2; Е(у): 0; 2; 3. 787. […]...
- Основні властивості числових нерівностей УРОК № 4 Тема. Основні властивості числових нерівностей Мета уроку: домогтися засвоєння учнями змісту поняття “оцінити значення виразу”; закріпити знання учнів про зміст властивостей числових нерівностей та їхніх наслідків. Продовжити роботу з вироблення вмінь: відтворювати зміст вивчених властивостей, наслідків із них і їх доведення; застосовувати властивості числових нерівностей та наслідки з них для розв’язування вправ […]...
- Теореми про ознаки паралелограма Урок № 6 Тема. Теореми про ознаки паралелограма Мета: сформувати в учнів свідоме розуміння змісту та схеми доведення теореми, що виражає ознаки паралелограма. Формувати вміння: – відтворювати ознаки та їхні доведення; – застосовувати вивчені ознаки для доведення того, що даний чотирикутник є паралелограмом. Тип уроку: засвоєння нових знань. Наочність та обладнання: конспект “Паралелограм”. Хід уроку […]...