Головна ⇒ 📌ГДЗ з математики ⇒ Ознаки рівнобедреного трикутника

Ознаки рівнобедреного трикутника

§ 2. Трикутники

9. Ознаки рівнобедреного трикутника

232. ?ABC – рівнобедрений, тому ВК є бісектрисою кута ABC, отже, ∠ABC = 2 х ∠ABK = 2 x 25° = 50°.

Ознаки рівнобедреного трикутника

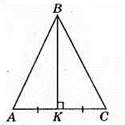
Відповідь: 50°.

233. BK є висотою та медіаною, тому? ABC – рівнобедрений, AB = ВС, отже, ∠C = ∠A =17°.

Ознаки рівнобедреного трикутника

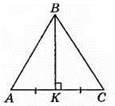
Відповідь: 17°.

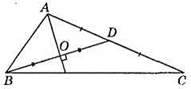
234. AС = ВС, тому ВК – бісектриса, ∠ACK = 1/2 • 90° = 45°, ∠KCB = 45°. Тому? АСК і? СКВ – рівнобедрені.

AK = KB = CK = 7 см, отже, AB = AK + KB = 7 + 7 = 14 (CM).

Ознаки рівнобедреного трикутника

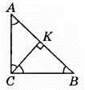
Відповідь: 14 см.

235. Оскільки AK = МК, то? АМК

– рівнобедрений, тоді ∠A = ∠AMК = ∠ACB. Оскільки ∠A = ∠ACB, то? АВС – рівнобедрений (AB = ВС).

236. Оскільки АK є бісектрисою і висотою трикутника ABC, то? ABC – рівнобедрений.

Ознаки рівнобедреного трикутника

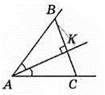
237. Оскільки? ABC – рівнобедрений, то ∠BAC = ∠BCA, тоді 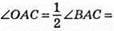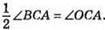Ознаки рівнобедреного трикутникаОзнаки рівнобедреного трикутника Оскільки ∠OAC = ∠OCA, то? АОС – рівнобедрений (АО = СО).

Ознаки рівнобедреного трикутника

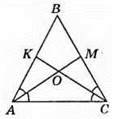
238. AB = ВС, АК = КС. АВ + ВС +АС = (AB + АК + ВК) + (BK + ВС + КС) – 2ВК = 16 + 16 – 2 x 5 = 32 – 10 = 22 (см).

Ознаки рівнобедреного трикутника

Відповідь: 22 см.

239. 1) Твердження не є правильним, на рисунку: AM – медіана, АН – висота, проте? ABC

– рівнобедрений (AB = ВС).

Ознаки рівнобедреного трикутника

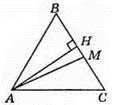
2) Твердження правильне.

240. ?АЕС = ?CFA за двома сторонами і кутом між ними (АС – спільна, 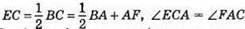Ознаки рівнобедреного трикутника). Із рівності трикутників випливає, що ∠EAC = ∠FCA, тоді? АМС – рівнобедрений.

Ознаки рівнобедреного трикутника

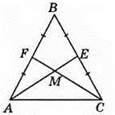
241. Нехай AB = ВС, AM = CK. ?АКС = ?СМА за вдома сторонами і кутом між ними (КС = АМ за умовою, АС – спільна, ∠KCA = ∠MAC, бо? АВС – рівнобедрений). Із рівності трикутників випливає, що ∠KAC = ∠MCA, тому? АМС – рівнобедрений.

Ознаки рівнобедреного трикутника

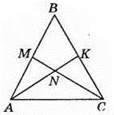
242. Нехай ∠FAC = ∠FCA, тоді? AFC – рівнобедрений, AF = FC.

?АЕС = ?CDA за двома сторонами і кутом між ними (AE = AF + FE = CF + FD = CD, АС – спільна, ∠EAC = ∠DCA). Із рівності трикутників випливає, що ∠ECA = ∠DAC, тобто? ABC – рівнобедрений.

Ознаки рівнобедреного трикутника

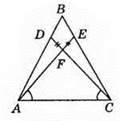
243. Оскільки у трикутнику АМD AF – бісектриса і висота, то? AMD – рівнобедрений, звідси AM = AD.

Оскільки у трикутнику BDK ВН – бісектриса і висота, то? BDK – рівнобедрений, звідси KB = DB.

Оскільки AM = AD, BK = DB і AD = BD за умовою, то AM = BK.

Ознаки рівнобедреного трикутника

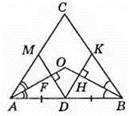
244. На рисунку: CM = MB, ∠ABK = ∠KBC, AM ⊥ BK. Оскільки у трикутнику ABM відрізок OB – бісектриса і висота, то? АВМ – рівнобедрений, тоді 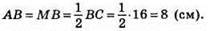Ознаки рівнобедреного трикутника

Ознаки рівнобедреного трикутника

Відповідь: 8 CM.

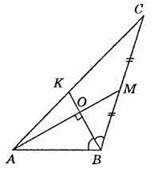
245. На рисунку: AD = DC, BO = OD, AK ⊥ BD. Оскільки AO – медіана і висота трикутника ABD, то? ABD – рівнобедрений і 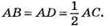Ознаки рівнобедреного трикутника Отже, AB : АС = 1 : 2.

Ознаки рівнобедреного трикутника

Відповідь: 1 : 2.

246.

Ознаки рівнобедреного трикутника

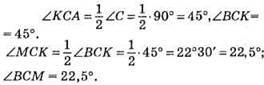
Оскільки? ACM (∠BCM = ∠B = 22,5°) – рівнобедрений, ВМ = MC.

Оскільки? CMA (∠MCK = 45° + 22,5° = 67,5°, ∠A = 67,5°) – рівнобедрений, то CM = МА.

Оскільки ВМ = MC, а MC = МА, то ВМ = МА, тобто М – середина AB.

247. Нехай AB = n см, ВС = (n + 2) см, АС = (n + 1) см. ВМ = MC, ∠ABL = ∠LBC, BL ⊥ AM.

Ознаки рівнобедреного трикутника

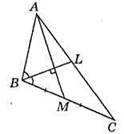
?АВМ – рівнобедрений, оскільки в ньому збігається бісектриса і висота, проведені з вершини В, тоді ВМ = AB = n, тоді MC = 2 см. Отже, AB = 2 см, ВС = 4 см, АС = 3 см.

Відповідь: 2 см, 3 см, 4 см.

248. ?СКМ – рівнобедрений (бо CF – бісектриса і висота), тоді КС = МС = 3 см.

?ADK – рівнобедрений (бо АН – бісектриса і висота), тоді AK = AD = АС – КС = 6 см – 3 см = 3 см. Тоді ВD = AB – AD = 5 – 3 = 2 (см).

Ознаки рівнобедреного трикутника

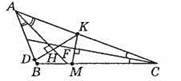
Відповідь: 2 см.

Вправи для повторення

249. На рисунку: AB = ВС = CD = DE = ЕР = х см. Тоді AB : CF = х : 2х = 1 : 2; AB : BF = х : 4х = 1 : 4; BD : AE = 2x : 4x = 1 : 2.

Ознаки рівнобедреного трикутника

Відповідь: 1 : 2, 1 : 4, 1 : 2.

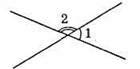
250. На рисунку: ∠1 – 420 = 1/2∠2. Нехай ∠1 = x°, ∠2 = 180° – x°, тоді x – 42 = 90 – x/2, звідси 2x – 84 = 90 – x; 3x = 174; x = 58. Отже, ∠1 = 58°, ∠2 = 122°.

Ознаки рівнобедреного трикутника

Спостерігайте, рисуйте, конструюйте, фантазуйте

251.

Ознаки рівнобедреного трикутника


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника Розділ 3. Трикутники. Ознаки рівності трикутників § 15. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника 351. 1) AT – висота трикутника ABC. 2) AN – медіана трикутника ABC. 3) АР – бісектриса трикутника? AВС. 352. Оскільки AK – висота, то ∠BKA = ∠CKA = 90°. 353. Оскільки АК – бісектриса, то ∠BAK = […]...

  2. Властивості й ознака рівнобедреного трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 12. Властивості й ознака рівнобедреного трикутника 476. На мал. 72: ML і МК – бічні сторони, KL – основа, ∠K = ∠L. 477. KD = DF, КЕ = EF, ∠K = ∠F, ∠KDE = ∠FDE, ∠DEK = ∠DEF = 90°. 478. Щоб провести бісектрису, медіану і […]...

  3. Ознаки рівнобедреного трикутника Геометрія Основні властивості найпростіших геометричних фігур Ознаки рівнобедреного трикутника Теорема 1. Якщо в трикутнику два кути рівні, то він рівнобедрений. Теорема 2. Трикутник рівнобедрений, ­якщо: – одна з його висот є медіаною; – одна з його медіан є бісектрисою; – одна з його висот є бісектрисою. Теорема 3. Трикутник рівнобедрений, ­якщо: – дві його висоти […]...

  4. Описане та вписане коло трикутника § 3. Паралельні прямі. Сума кутів трикутника § 20. Описане та вписане коло трикутника 540. 1) Різносторонній гострокутний трикутник. 2) Прямокутний трикутник. 3) Тупокутний трикутник. 541. 1) Рівнобедрений гострокутний трикутник. 2) Рівнобедрений тупокутний трикутник. 542. 543. 544. Вправи 545. Медіана BD рівнобедреного трикутника ABC є в той же час і серединним перпендикуляром до сторони АС […]...

  5. Ознаки паралельності двох прямих § 3. Паралельні прямі. Сума кутів трикутника 13. Ознаки паралельності двох прямих Практичні завдання 300. 1) Кути АОМ і CEO – відповідні; 2) кути АОЕ і СЕК – відповідні; 3) кути АОE і OED – різносторонні; 4) кути АОЕ і CEO – односторонні. 1) відповідні; 2) односторонні; 3) різносторонні. 301. 1) ∠1 i ∠5; ∠2 […]...

  6. Сума кутів трикутника. Нерівність трикутника § 3. Паралельні прямі. Сума кутів трикутника § 15. Сума кутів трикутника. Нерівність трикутника Вправи 357. Нехай х° – третій кут трикутника, тоді 35 + 96 + х = 180, звідси х + 131 = 180; х = 180 – 131; х = 49. Отже, третій кут дорівнює 49°. Відповідь: 49°. 358. Нехай х° – […]...

  7. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 19. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників 466. 1) PF – гіпотенуза, PL і LF – катети. 2) PF довша за PL, PF довша за LF, оскільки PF – гіпотенуза. 467. На рис. 321 трикутники рівні за двома катетами. Оскільки АС = ML, СВ = LP, […]...

  8. Властивість медіани, бісектриси й висоти рівнобедреного трикутника Урок № 25 Тема. Властивість медіани, бісектриси й висоти рівнобедреного трикутника Мета: домогтися свідомого сприйняття учнями змісту теореми про властивість медіани, бісектриси й висоти рівнобедреного трикутника та наслідків з неї; сформувати вміння відтворювати названі властивості та застосовувати їх під час розв’язування задач. Тип уроку: засвоєння знань, умінь та навичок. Наочність і обладнання: набір демонстраційного креслярського […]...

  9. Зовнішній кут трикутника та його властивості Розділ 3. Трикутники. Ознаки рівності трикутників § 18. Зовнішній кут трикутника та його властивості 438. ∠BAK – зовнішній кут при вершині А. 439. ∠LDP – зовнішній кут при вершині D. 441. ∠A + ∠B = 70° – за властивістю зовнішнього кута трикутника. 442. Зовнішній кут трикутника при вершині С дорівнює 74° згідно з властивістю зовнішнього […]...

  10. Властивості прямокутного трикутника § 3. Паралельні прямі. Сума кутів трикутника § 17. Властивості прямокутного трикутника 457. Найбільший катет трикутника дорівнює 24 см. 458. ?DEF – прямокутний, ∠F = 90°, ∠D = 30°, DE = 18 см. Відповідь: 9 см. 459. ?KCM – прямокутний, ∠M = 90°, ∠C = 60°, MC = 7 см. ∠MKC = 90° – 60° […]...

  11. Рівні трикутники. Висота, медіана, бісектриса трикутника § 2. Трикутники 6. Рівні трикутники. Висота, медіана, бісектриса трикутника Практичні завдання 132. 133. ВН – спільна висота трикутників ABD, ABC, BDC. ВН лежить поза трикутником BCD. 134. 135. 136. Вправи 137. 1) ME; 2) ∠E; 3) MK i KE; 4) ∠K i ∠E. 138. 1) ∠E; 2) ∠C i ∠E;3) CF; 4) CF і […]...

  12. Властивості кутів трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 10. Властивості кутів трикутника 344. ∠E = 60°, ∠F = 40°, ∠D = 80°. ∠E + ∠F + ∠D = 60° + 40° + 80° = 180°. 345. На мал. 208 неправильно сказано градусну міру кутів? АВС, оскільки? ABC – прямокутний, a ∠B + ∠C = […]...

  13. Ознаки рівності прямокутних трикутників Розділ 1. Найпростіші геометричні фігури та їх властивості § 14. Ознаки рівності прямокутних трикутників 549. Ні, трикутники не рівні. 550. Мал. 319. ?САВ = ?HDQ (за катетом і гострим кутом: CA = HD, ∠C = ∠H). Мал. 320. ?ABC = ?CDA (за гіпотенузою АС і гострим кутом: ∠BAC = ∠DAC). Мал. 321. ?АОВ = ?DCО […]...

  14. Вправи 425-474 425. АС – основа; AB = CB; ∠ADC = 150°. ∠CAD = ∠BAD = x; ∠ACD = 2x; x + 2x + 150° = 180°; 3x = 180° – 150°; 3x = 30°; x = 10°; ∠C = ∠A = 20°; ∠B = 180° – (20° + 20°) = 140°. Відповідь: 20°, 20°, 140°. 426. […]...

  15. Рівнобедрений трикутник і його властивості § 2. Трикутники 8. Рівнобедрений трикутник і його властивості Практичні завдання 196. 197. 198. Вправи 199. 1) Р = 13 + 2 х 8 = 29(см). Відповідь: 29 см. 2) Нехай х см – бічна сторона, тоді 15 + 2х = 39, тоді 2х = 39 – 15; 2х = 24; х = 24 : […]...

  16. Ознаки паралельності прямих. Сума кутів трикутника Урок № 40 Тема. Ознаки паралельності прямих. Сума кутів трикутника Мета: перевірити рівень засвоєння знань та вмінь, передбачених програмою, із зазначених тем. Тип уроку: контроль та корекція знань. ХІД УРОКУ I. Організаційний момент II. Перевірка домашнього завдання Зібрати зошити з виконаною домашньою контрольною роботою. Роботу оцінити та врахувати в тематичному балі. III. Умова контрольної роботи […]...

  17. Перша та друга ознаки рівності трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 13. Перша та друга ознаки рівності трикутників 301. На рис. 227 трикутники рівні за першою ознакою (за двома сторонами і кутом між ними). На рис. 228 трикутники рівні за другою ознакою (за стороною і прилеглими двома кутами). 302. У? ABC і? CDA спільний елемент – сторона AВ. У? […]...

  18. Вправи 275-324 275. Кут В. а) ВА = ВС, ?АВС – рівнобедрений, у нього дві сторони рівні; Б) ∠A = ∠C. 276. ∠A = 60°; AD – бісектриса кута А. BC ⊥ AD; AB = AC; ∠B = ∠C. 277. AB = ВС; АС – основа. Нехай АВ = ВС = х м, тоді АС = (х […]...

  19. Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих Розділ 2. Взаємне розміщення прямих па площині § 9. Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих 170. Рис. 119: ∠1 і ∠2 – внутрішні різносторонні кути. Рис. 120: ∠1 і ∠2 – відповідні кути. Рис,121: ∠1 i ∠2 – внутрішні різносторонні кути. 171. Внутрішні односторонні кути: ∠ANM і ∠NMB, ∠CNM і ∠NMD. […]...

  20. Дотична до кола, її властивості Розділ 4. Коло і круг. Геометричні побудови § 22. Дотична до кола, її властивості 607. Проведемо радіус ОР, а потім за допомогою косинця побудуємо пряму m, перпендикулярну до радіуса. За теоремою 2 пряма m є дотичною до кола. 608. Проведемо радіус ОМ, а потім за допомогою косинця побудуємо пряму n, перпендикулярну до радіуса. За теоремою […]...

  21. Кут. Вимірювання кутів. Бісектриса кута Розділ 1. Елементарні геометричні фігури та їхні властивості § 3. Кут. Вимірювання кутів. Бісектриса кута 33. 1) М – вершина кута, МА і МК – сторони кута АМК; 2) L – вершина кута, LP і LF – сторони кута PLF; 3) N – вершина кута, NB i NC – сторони кута BNC. 34. 1) O […]...

  22. Вправи 475-524 475. ?ABC – прямокутний; ∠A = 30°; АС = 18 см; ВК – бісектриса, проведена до катета АС; ∠CBK = ∠ABK = ∠CBA : 2 = 60° : 2 = 30°; ∠CBA = 90° – ∠CAB = 90° – 30° = 60°; СК = х, тоді AK = 18 – х. ?АВК – прямокутний; ∠A […]...

  23. Властивості кола. Дотична до кола § 3. Паралельні прямі. Сума кутів трикутника § 19. Властивості кола. Дотична до кола Практичні завдання 507. АК = КВ. 508. AB ⊥ CD – дотичні до кола. 509. АС i ВС – дотичні до кола. 510. Таких кіл може бути два. Вправи 511. CD ⊥ AB. ?АОК = ?ВОК (за катетом і гіпотенузою: ОК […]...

  24. Медіана, бісектриса і висота трикутника Урок № 24 Тема. Медіана, бісектриса і висота трикутника Мета: домогтися засвоєння учнями: – змісту понять “медіана трикутника”; “бісектриса трикутника”; “висота трикутника”; – уявлення про положення висот у різних видах трикутника. Сформувати вміння: – зображати медіани, висоти та бісектриси трикутника; – розрізняти ці відрізки, виходячи з умови задачі. Тип уроку: застосування знань, умінь та навичок. […]...

  25. Трикутник і його елементи Розділ 1. Найпростіші геометричні фігури та їх властивості § 9. Трикутник і його елементи 292. На мал. 194 зображені трикутники ABD, ABC, ОВС. Проти кута C в трикутнику АВС лежить сторона АB, в трикутнику DBC – сторона BD. Прилеглими до кута С в трикутнику ABC є сторони АС і ВС, в трикутнику DBC – сторони […]...

  26. Коло і круг Розділ 1. Найпростіші геометричні фігури та їх властивості § 15. Коло і круг 588. 1) Хордами є відрізки: KB, NC, KN, CB, LD. 2) Діаметрами є відрізки: LD, NC, КВ. 3) Радіусами кола є відрізки: OL, OK, ОС, OD, OB, ON. 589. Дотичні до кола: АС, CB, AB. ON ⊥ AC, ОМ ⊥ CB, OK […]...

  27. Взаємне розміщення двох кіл Розділ 4. Коло і круг. Геометричні побудови § 25. Взаємне розміщення двох кіл 656. На рис. 404 кола перетинаються. На рис. 405 кола дотикаються. На рис. 406 кола не мають спільних точок. 657. 1) Кола мають внутрішній дотик. 2) Кола перетинаються. 3) Кола концентричні. 658. 1) Кола мають зовнішній дотик. 2) Кола не перетинаються. 659. […]...

  28. НЕРІВНОСТІ ТРИКУТНИКА РОЗДІЛ 3 ТРИКУТНИКИ & 15. НЕРІВНОСТІ ТРИКУТНИКА Ви вже знаєте, що кожна сторона трикутника менша від суми двох інших його сторін. Щоб довести це твердження як теорему, спочатку розглянемо іншу теорему. Теорема 19 У кожному трикутнику проти більшої сторони лежить більший кут, а проти більшого кута – більша сторона. Доведення. 1) Нехай у трикутнику ABC […]...

  29. Вправи 525-574 525. АВ = CD; AO : OB = CO : OD; ?СОВ = ?AOD (за двома сторонами і кутом МІНІ ними). З рівності трикутників маємо: BC = AD. ?ВСА = ?DAC. 1) АС – спільна сторона; 2) AB = CD; 3) BC = DA; ∠MCA = ∠MAC; отже, ∠A = ∠C; ?CMА – рівнобедрений; МС […]...

  30. Вправи 150-175 150. ∠1 = 90°, ∠2 = ∠1 = 90° – вертикальні кути; ∠3 – суміжний куту ∠1. ∠3 = 180° – 90° = 90°, ∠3 = ∠4 = 90° (вертикальні кути). 151. ∠(ac) = 70°; ∠(ab) = 90°; ∠(bc) = 90° – ∠(ac) = 90° – 70° = 20°. 152. а ⊥ с; ∠(ab) = […]...

  31. Рівнобедрений трикутник Геометрія Основні властивості найпростіших геометричних фігур Рівнобедрений трикутник Трикутник називається Рівнобедреним, якщо у нього дві сторони рівні. Ці сторони називаються Бічними сторонами, а третя сторона – Основою трикутника. На рисунку: ABC – рівнобедрений трикутник; – бічні сторони; AC – основа. Теорема 1. У рівнобедреному трикутнику кути при основі є рівними. Теорема 2. У рівнобедреному трикутнику […]...

  32. Властивості конуса 1. 1) Твірна конуса не може утворювати з його основою прямий кут, оскільки Вона є гіпотенузою трикутника обертання, яка утворює бічну поверхню конуса. 2) Теж не може (обгрунтування у п. 1). Якщо конус зрізаний 1) ні; 2) так. Відповідь: 1) ні; 2) ні для зрізаного конуса 1) ні, 2) так. 2. Нехай SA – твірна […]...

  33. Суміжні та вертикальні кути § 1. Найпростіші геометричні фігури та їхні властивості § 4. Суміжні та вертикальні кути Практичні завдання 86. ∠BAC – гострий, ∠OAB – суміжний до кута ВАС. ∠АОВ – прямий, ∠COA – суміжний до кута АОВ. ∠BOC – тупий, ∠AOB – суміжний до кута ВОС. 87. ∠AOC і ∠COB – суміжні. 88. а) ∠ABD i ∠CBD; […]...

  34. Коло і його елементи Розділ 4. Коло і круг. Геометричні побудови § 21. Коло і його елементи 578. PL – хорда, що проходить через центр кола, називається діаметром. 579. 1) 5 х 2 = 10(см); 2) 4,7 х 2 = 9,4 (дм). 580. 1) 8 мм х 2 = 16 мм; 2) 4,8 см х 2 = 7,6 см. […]...

  35. Промінь. Кут. Вимірювання кутів § 1. Найпростіші геометричні фігури та їхні властивості 3. Промінь. Кут. Вимірювання кутів Практичні завдання 49. Промені AB і АС – не доповняльні. Промінь AN – доповняльний до променя AB, а промінь AM – доповняльний до променя АС. На рисунку зображено промені АB, АС, AN, AM. 50. Промені AB і ВА не е доповняльними, оскільки […]...

  36. Вправи 375-424 375. ВС – бісектриса ∠ABD; ∠ABD = 80° + 80° = 160°; ∠BAC + ∠ABD = 20° + 160° = 180°; ∠BAC і ∠ABD – внутрішні односторонні кути при прямих АС і BD та січній АВ. Отже, BD || АС. 376. ∠A = 70°, ∠B = 40°, BE – бісектриса ∠ABD; ∠DBE = ∠ABE = […]...

  37. Знаходження площі трикутника за двома сторонами і кутом між ними УРОК № 12 Тема. Знаходження площі трикутника за двома сторонами і кутом між ними Мета уроку: виведення формули для знаходження площі трикутника за двома сторонами і кутом між ними. Формування вмінь застосовувати виведену формулу до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Співвідношення між сторонами і кутами трикутника”[13]. Вимоги до рівня підготовки учнів: […]...

  38. Ознаки паралельності прямих Урок № 30 Тема. Ознаки паралельності прямих Мета: закріпити знання учнів про ознаки паралельності двох прямих (за кутами, що утворилися при перетині даних прямих січною). Сформувати вміння: – визначати вид двох кутів, що утворилися при перетині двох прямих січною; – за певним співвідношенням цих кутів робити висновок щодо паралельності прямих; – для встановлення співвідношення кутів […]...

  39. СУМА КУТІВ ТРИКУТНИКА РОЗДІЛ 3 ТРИКУТНИКИ & 10. СУМА КУТІВ ТРИКУТНИКА Теорема 8 Сума кутів трикутника дорівняй: 180°. Доведення. Нехай ABC – довільний трикутник (мал. 130). Через йот вершину С проведемо пряму КР, паралельну стороні АВ. Утворені кути АСК і ВСР позначимо цифрами 1 і 2. Тоді ∠A = ∠1, ∠B = ∠2, як внутрішні різносторонні кути при […]...

  40. Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої Розділ 2. Взаємне розміщення прямих па площині § 7. Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої 128. m ⊥ n, MN ⊥ АВ. 129. KA ⊥ c, ВМ ⊥ с. 130. ВL ⊥ a. MВ ⊥ a. 131. 1) Відрізки AB і MN перпендикулярні, оскільки вони лежать на перпендикулярних прямих a і b. 2) […]...

Ви зараз читаєте: Ознаки рівнобедреного трикутника
«
»