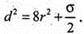Паралелепіпеди
748.
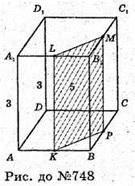
Нехай дано ABDCA1B1D1C1- прямий паралелепіпед; K, L, М – середини ребер АВ, Α1Β1, В1C1.
Проведемо МР? LK, KLMP – переріз паралелепіпеда площиною, яка проходить через точки K, L, М. KLMP – прямокутник.
LK + AB, LM? KР, LK? МР.
Площа KLMP = LK × КР, LK = АА1 = 3.
ΔLKM – прямокутний, LM2= KМ2 – LK2 = 25 – 9 = 16;
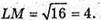
Sпер.=3 × 4 = 12 (см2).
Відповідь: 12 см2.
749.
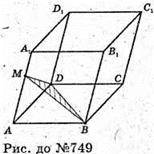
Нехай дано похилий паралелепіпед ABDCA1B1D1C1, Μ – середина ребра АА1. З’єднаємо точки M і D, вони належать
З’єднаємо точки М і В, вони належать площині АА1В1.
ΔMDB – переріз, який проходить через точки M, D, В.
750.
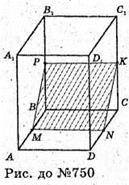
Нехай дано паралелепіпед ABDCA1B1D1C1. Переріз проходить через середини ребер AB, DC, ВВ1. Μ – середина ребра AB, N – середина ребра CD. Р – середина ребра ВВ1. З’єднаємо точки M і Р, М і N (ці точки лежать в одній площині). Через точку Р проведемо пряму РК? MN. MPKN – переріз.
А) якщо паралелепіпед прямокутний, то цей переріз є прямокутником;
Б) якщо прямий, то переріз – паралелограм;
В) якщо похилий, то переріз – паралелограм.
751.
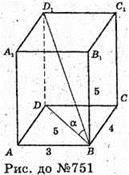
Нехай дано прямокутний паралелепіпед, виміри якого АВ = 3 см, ВС = 4 см,
ВВ1 = 5 см. Грань ABCD має найменшу площу. ∠D1BD – кут нахилу діагоналі паралелепіпеда до площини ABCD.
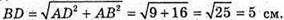
BDB1D1 – квадрат. Отже, ∠DBD1 = 45°, ∠DBB1 = 90°, BD1 – бісектриса прямого кута.
Відповідь: 45°.
752.
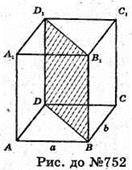
Нехай дано прямокутний паралелепіпед. Його діагональний переріз – квадрат. BD = В1В = с, тоді а2 + Ь2 = с2.
Відповідь: а2 + b2 = с2.
753.
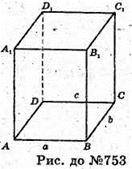
Нехай дано прямокутний паралелепіпед, у якого SABCD= 42 см2; SBB1C1C = 79 см2;
SAA1B1B = 84 см2·
Нехай виміри прямокутного паралелепіпеда АВ = а, ВС = b, ВВ1 = с.
За умовою маємо:
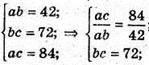
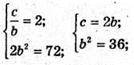
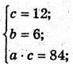
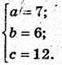
Відповідь: 6 см, 7 см, 12 см.
754.
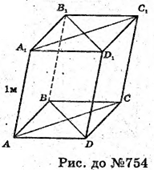
Нехай дано прямий паралелепіпед, сторони його основи AD = 2,3 м; АВ = 1,1 м; ∠ВАD = 60°; АА1 = 1 м.
ABCD – паралелограм, BD2 = АВ2 + АD2 – 2АВ × АD × cos 60° (за теоремою косинусів).
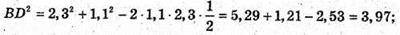
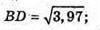
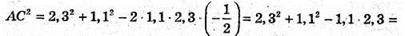
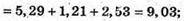
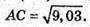
AA1C1C – діагональний переріз.
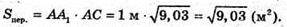
ВВ1D1D – діагональний переріз.
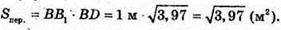
Відповідь: 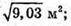
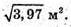
755.
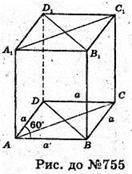
Нехай дано прямий паралелепіпед, всі ребра якого дорівнюють а;
АВ = ВС = DС = АD = АА1 = а. ∠DАВ = 60°. Знайдемо діагоналі основи ABCD.
ΔABD – рівносторонній. АВ = AD = ВD = а.
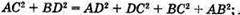
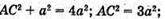
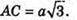
ΔDD1В – прямокутний, ∠D1DB = 90°;
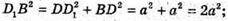
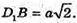
ΔАСС1 – прямокутний, ∠С1СА = 90°.
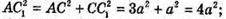
AC1 = 2а.
Відповідь: 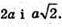
756.
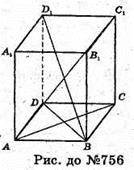
Нехай дано прямий паралелепіпед, сторони основи якого 6 см і 8 см, а одна з діагоналей основи 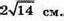 Бічне ребро АА1 = 5 см,
Бічне ребро АА1 = 5 см, 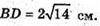
Знайдемо діагональ АС основи.
AC2 + BD2 = AD2 + DC2 + BC2 + AB2
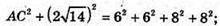
АС2 + 56 = 72 + 64 + 64; АС2 = 144; 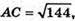 АС = 12.
АС = 12.
ΔACC1 – прямокутний, ∠ACC1 = 90°;
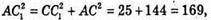 АС1 = 13 см.
АС1 = 13 см.
ΔBDD – прямокутний, ∠D1DB = 90°.
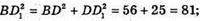 BD1= 9 см.
BD1= 9 см.
Відповідь: 9 см і 13 см.
757.
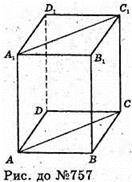
Нехай дано прямий паралелепіпед, основою якого є паралелограм зі сторонами АВ= 3 см, AD = 5 см, ∠DAB = 60°, SперерізуAA1C1C = 42 см2 – площа більшого діагонального перерізу. Знайдемо більшу, діагональ основи.
АС2 = АВ2 + ВС2 – 2АВ × ВС × cos 120° (за теоремою косинусів).
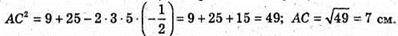
SперерізуAA1C1C = AC × C 1C; 42 = C1C × 7; C1C = 6 см;
Sповне = 2Sосн. + Sбічн.
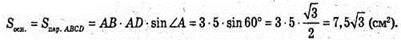
Sбічн. = Pосн. × АA1 = (3 + 5) × 2 × 6 = 96 (см2).
Відповідь: 
758.
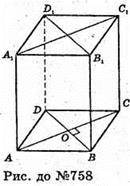
Нехай дано прямий паралелепіпед, в основі якого лежить ромб ABCD.
AB = ВС = CD = AD = a; SперерізуAA1C1C = 9 см2;
SперерізуDD1B1B = 12 (см ), Sбічн. парал. = PABCD × CC1,
Де = PABCD периметр ромба, CC 1 – висота паралелепіпеда.
Нехай АС = d1, BD = d2, 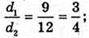 d1 = Зх; d2 = 4х;
d1 = Зх; d2 = 4х;
Δ ВОС – прямокутний. BO + ОС; 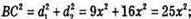
ВС = 5x; S бічне = P осн. × h = 20x × h; Saa1c1c = АС × C1C = 6x × h;
9 = 6х × h; 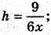
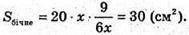
Відповідь: 30 см2.
759.
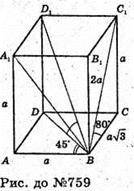
Нехай дано прямокутний паралелепіпед, діагоналі бічних граней утворюють з площиною основи кути 30° і 45°. Діагональ ВС1 утворює з площиною основи
∠C1 BC = 30°. Діагональ А1В утворює з площиною основи ∠Α1ΒΑ = 45°.
ΔΑ1АВ – прямокутний рівнобедрений.
Нехай А1А = АВ = а. ΔС1СВ – прямокутний, ∠C1BC = 30°.
С1C = а; 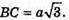 ΔABD – прямокутний.
ΔABD – прямокутний.
BD2 = АВ2 + AD2 = а2 + 3а2 = 4а2; BD = 2а.
Розглянемо ΔDD1В, 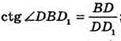
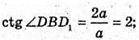 ∠DBD1 = arcctg2.
∠DBD1 = arcctg2.
Відповідь: arcctg2.
760.
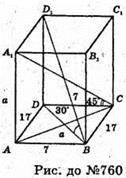
Нехай дано прямий паралелепіпед, у якого сторони основи дорівнюють
АВ = 7 см, ВС = 17 см. Діагональ BD1 утворює з площиною основи ∠D1BD = 30°.
Діагональ А1С утворює з площиною основи кут ∠A1CA = 45°,
ΔA1AC – прямокутний. ∠A1AC = 90°. АС = А1А = a.
ΔDD1В – прямокутний. DD1 = a; BD1 = 2а; BD2 = 4а2 – а2 = 3а2; 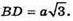
За властивістю діагоналей паралелограма маємо: АС2 + DB2 = 2AD2 + 2АВ2;
А2 + 3а2 = 172 + 172 + 72 + 72; 4а2 = 289 × 2 + 49 × 2; 4а2 = 578 + 98; 4а2 = 676;
А2 = 169; а = 13. BD1 =2 × 13=26см; 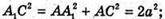
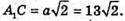
Відповідь: 26 см і 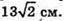
761.
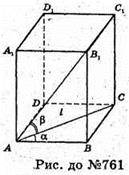
Нехай рано прямокутний паралелепіпед, діагональ основи якого дорівнює
АС = l і утворює зі стороною основи ∠CAB = α, а з діагоналлю паралелепіпеда АС1 ∠C1AC = β. Sбічн. пар. = Росн. × h, де Росн. = 2АВ + 2АС. h = CC1.
ΔАВС – прямокутний. АВ = l × cos α; ВС = l sin α;
Росн. = 2l cos α + 2l sin α = 2l(sin α + cos α).
ΔACC1 – прямокутний, СС1 = l × tg β. S бічн. = 2l2 tg β(sin α + cos α).
Відповідь: 2l 2 tg β(sin α + cos α).
762.
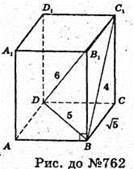
Нехай дано прямокутний паралелепіпед ABCDA1B1C1D1, у якого
DB1 = 6 см, DB = 5 см, ВС1 = 4 см.
ΔDBB1 – прямокутний. ∠DBB1 = 90°;
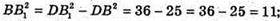
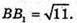
ΔCC1B – прямокутний, ∠BCC1= 90°;
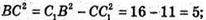
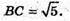
ABDC – прямокутний, DC2 = ВD2 – ВС2 = 25 – 5 = 20;
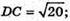
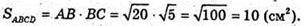
Відповідь: 10 см2.
763.
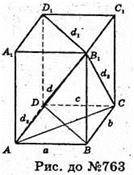
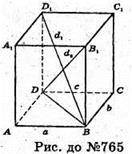
Нехай дано прямокутний паралелепіпед ABCDA1B1C1D1, d 1 – діагональ грані A1B1C1D1; d2- діагональ грані ВВ1С1C; d3- діагональ грані АА1В1В; d – діагональ прямокутного паралелепіпеда.
Нехай АВ = а, ВС = b, ВВ1 = с.
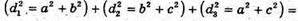
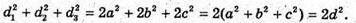
D2 = а2 +b2 + с2, звідки d2 = 0,5(d12 + d22 + d32), що й треба було довести.
764.
 а) ні; б) ні.
а) ні; б) ні.
765.
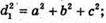
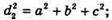
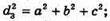
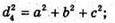
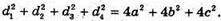
767.
Прямокутний паралелепіпед не можна перетнути площиною так,
Щоб у перерізі утворився прямокутний трикутник.
768.
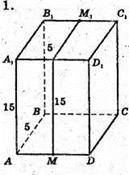
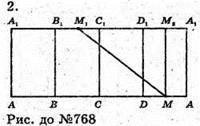
ABCDA1B1C1D1 – правильна призма, у якої АА1 = 15 см, АВ = 5 см.
ΔΜ1Μ2Μ – прямокутний. М2М = 15; М1М 2 = 10.
Μ1М2 = 152 + 102 = 225 + 100 = 325; 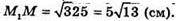
769.
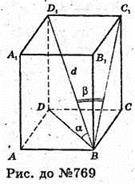
Нехай дано прямокутний паралелепіпед, діагональ якого дорівнює d,
BD1 = d і утворює з площиною основи кути
∠DBD1 = α, а з площиною бічної грані – кут β.
ΔDD1B – прямокутний, ∠D1DB = 90°, DD1 = d × sin α; BD = d × cos α.
ΔD1С1В – прямокутний, ∠D1C1B = 90°, D1C1 = d × sin β. ΔABD – прямокутний. За теоремою Піфагора маємо: AD2 = BD2- AB2= d2 cos2 α – d2 sin β.
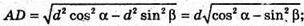
Sбічної поверхні = Pосн × h, де Pосн = 2AB + 2BC, h = CC1;
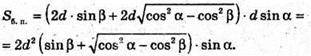
770.
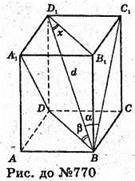
Нехай дано прямокутний паралелепіпед, діагональ якого BD утворює з бічними гранями кути α і β. ∠C1BD = α, ∠DBA1 = β.
∠BD1B1 = x, кут, який ця діагональ утворює з площиною основи.
Нехай ВВ1 = d.
ΔBC1B1 – прямокутний; B1C1 = d × sin α.
ΔΑ1Β1Β – прямокутний; A1D1 = d × sin β.
ΔA1D1B1 – прямокутний; 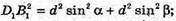
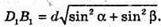
ΔD1Β1Β- прямокутний. 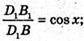
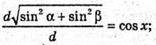
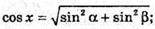
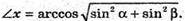
771.
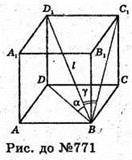
Нехай дано прямий паралелепіпед, основою якого є ромб ABCD.
BD1 – діагональ паралелепіпеда, BD1 = l, ∠DBD1 = α – кут між діагоналлю l і площиною основи. ∠D1BC1 = φ – кут між діагоналлю l і площиною бічної грані. ΔDB1B – прямокутний. ∠D1DB = 90°. DD1 = l × sin α; BD = l × cos α.
ΔBD1C1 – прямокутний. ∠BC1D1 = 90°; D1C1 = І × sin φ.
ΔABD – прямокутний; AD2 = BD2 – AB2; AD2 = l cos2 α – l sin2 φ;
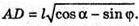
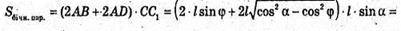
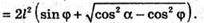
Відповідь: 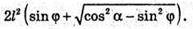
772.
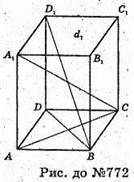
Нехай дано прямий паралелепіпед, з основою ABCD, сторони якого AB = 8 см, ВС = 10 см. Діагональ BD1 = 14 см, діагональ A1C = 16 см, АС і BD – діагоналі основи паралелепіпеда.
За властивістю діагоналей паралелограма:
АС2 + BD2 = 2АВ2 + 2ВС2; АС2 + ВВ2 = 2 × 64 + 2 × 100;
АС2 + ВВ2 – 128 + 200 = 328.
ΔАА1С – прямокутний; 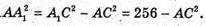
ΔDD1B – прямокутний; 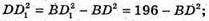
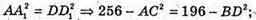 АС12 – BD12 = 256 – 196;
АС12 – BD12 = 256 – 196;
АС2 – BD2 = 60.
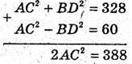
АС2 = 194; 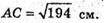
194 = BD2= 60; ВD2 = 134; 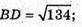
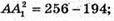
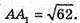
Sбічн. = PABCD× H, де AA1.
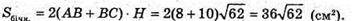
Відповідь: 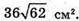
773.
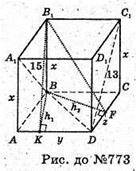
Нехай дано прямий паралелепіпед ABCDA1B1C1D1, в якому
DA1 = 15 см, DC1 = 13 см. ВК + AD; В1K + AD; 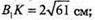
H2 + BC; BF + DC; B1F + DC; 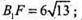
H1 і h2 – висоти паралелограма ABCD.
Нехай AA1 = х, AD = у, DC = z.
Х2 + у2 = 225 ; х2 + z2 =169 .
ΔΒΒ1F: 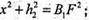
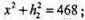
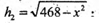
ΔΒ1BK: 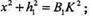
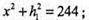
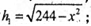
SABCD = ВK × AD = BF × DC ;
H1× y = h2 × z,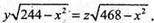
У2 = 225 – х2; 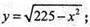
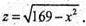
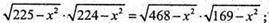
(225 – x2 )(224 – х2) = (468 – х2) (169 – х2);
54900 – 225х2 – 244х2 + х4 = 79092 – 468х2 – 169х2 + х4 – 225х2 – 244х2 +
+ 468х2 + 169х = 79092 – 54900;
168х2 = 24192; х2 = 144; х = 12;
122+ y = 225; у2 =225 -144 = 81; y = 9;
144 + z2 = 169; z2 = 25; z = 5.
S бічн. ABCDA1B1C1D1 = Pосн. × H; H = СС 1 = х = 12 см,
Де Pосн.= 2(z + y) = 2(9 + 5) = 28 (см).
Sбічн. =28 × 12 = 336 (см2).
Відповідь: 336 см2.
774.
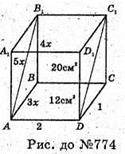
Нехай дано прямий паралелепіпед ABCDA1B1C1D1.
Проведемо переріз AB1C1D. SABCD =12 см2; SAB1C1D = 20 см2;
SABC = AD × AB; AD × AB = 12; SAB1C1D = AD × AB1; AD × АВ1 = 20;
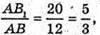 AB1 = 5x, AB = 3x, тоді ВВ1 = 4х,
AB1 = 5x, AB = 3x, тоді ВВ1 = 4х, 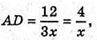 BC = AD.
BC = AD.
А) 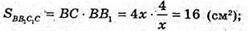
Б) AD : DC = 2 : 1. SΔA1B1C; 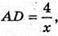
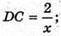
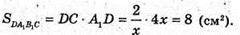
775.
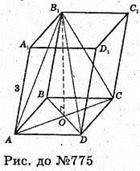
Основою паралелепіпеда є квадрат зі стороною 4 см.
АВ = ВС = CD = AD = 4 см.
Одна з вершин основи В1 рівновіддалена від вершин другої основи.
В1B = B1D = В1C = В1A; АА1 = ВВ1 = С1С = D1D = 3 см.
BD і АС – діагоналі квадрата зі стороною 4 см.
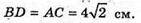
ΔBB1O – прямокутний. 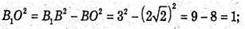
Β1Ο = 1 см; 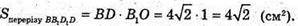
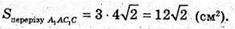
Відповідь: 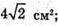
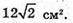
776.
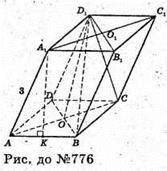
Нехай дано паралелепіпед ABCDA1B1C1D1, у якого основа – квадрат ABCD.
AB = BC = CD = AD = AA1=BB1= CC1 = DD1 = а.
∠A1AB = ∠A1AD = 60°
AA1 ? BB1 ? DD1 ? CC1.
ABCD – квадрат. BD + АС. О – точка перетину діагоналей квадрата ABCD.
Проведемо OK + А В, A1K + АВ за теоремою про три перпендикуляри.
ΔAA1K – прямокутний, ∠Α,ΑΚ = 60°; 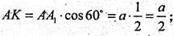
Отже, проекцією точки А1 буде точка О.
A1O + ABCD.
ΔDD1B – рівнобедрений, за умовою OD = ОВ.
DO – медіана; ОС + BD, отже D1O + BD,
D1O – висота; DD1 = BD1 = a.
Відповідь: BD1 = а.
777.
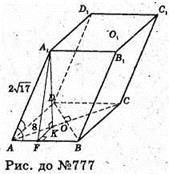
Нехай дано паралелепіпед ABCDA1B1C1D1 , бічне ребро 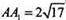
І утворює зі сторонами рівні кути: ∠A1AB = ∠A1AD.
Висота А1K + АС; A1K = 2 см;
ABCD – ромб із діагоналями АС = 20 см; BD = 15 см.
Sповн. ABCDA1B1C1D1 = Sбічне + Sосн.
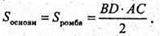
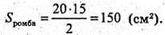
ΔΑΑ1Κ: ΑΚ2+ Α21K2 = Α1Α2;
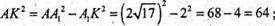 ΑΚ = 8,
ΑΚ = 8,
ΔΑΟΒ – прямокутний, 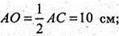
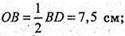
AB2 =AO2 + OB2= 100 + 56,25 = 156,25 ; ΑΒ = 12,5 см.
ΔAFK ~ ΔAOB; 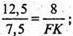 FK = 4,8;
FK = 4,8;
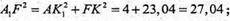 Α1F = 5,2 см.
Α1F = 5,2 см.
S бічн. = PABCD × A 1F = 4 × 12,5 × 5,2 = 260 (см 2).
S повн. = S6ічн.+2Sоснов. = 260 + 2 × 150 = 560 (см 2).
Відповідь: 560 см 2.
778.
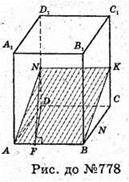
Нехай дано прямий паралелепіпед, в основі якого лежить ромб зі стороною
2 см.
АВ = ВС = DC = AD = 2a;
∠DAB = 30°.
Через сторону основи прямого паралелепіпеда проведено січну площину
ABKN під кутом 60° до площини основи. ∠NFD = 60°.
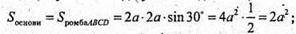
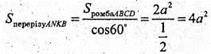
Відповідь: 4а2.
779.
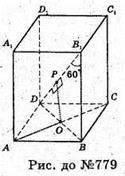
Нехай дано прямий паралелепіпед ABCDA1B1C1D1.
Діагональ Β 1Ο утворює з бічним ребром В1В кут ∠ΟΒ1Β = 60°.
В1D і AA1 мимобіжні прямі. Β1D віддалена від AA1 на АО = 3 см.
AО + ВD; AО + площині DВ1В; AO + DB.
DВ1 і АС – мимобіжні прямі. Β1D віддалена від прямої АС
На відстань ОР = 2 см. ОР + АС; OP + Β1Ο.
ΔDΒ1Β – прямокутний, В1В + ВD, ∠DΒ1Β = 60°; ∠Β1DΒ = 30°;
Δ DPO – прямокутний, ∠PDO = 30°;
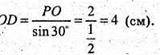
ΔAOD – прямокутний, AD2 = OD2 + AO2; AD2 = 16 + 9 = 25; AD = 5 см.
ABCD – ромб, BD + AС; BD = 20D = 8 см; AO × 2 = AC = 6 см.
Площа повної поверхні дорівнює:
Sповн. = 2S осн. + S бічн. ABCDA1B1C1D1
ΔΒ1ΒD – прямокутний;
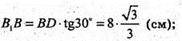
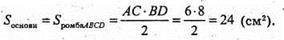
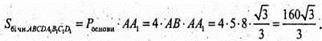
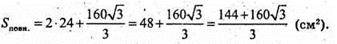
Відповідь: 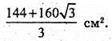
780.
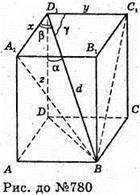
Нехай дано прямокутний паралелепіпед, діагональ BD1
Утворює з його ребрами кути α, β, γ.
A1D1 = х; D1C1 = у; DD1 = z; BD1 = d.
Z = d × cos α; у = d × cos γ; x = d × cos β; d2 = x2 + y2 + z2;
D2 = d2 cos2α + d2 cos2β + d2 cos2γ.
Поділимо на d2
1 = cos2α + cos2β + cos2γ, що й треба було довести.
781.
Нехай діагональ прямокутного паралелепіпеда утворює з трьома його ребрами кути α, β, γ. а, β, γ – гострі кути прямокутного трикутника, α + β + γ < 180°.
782.
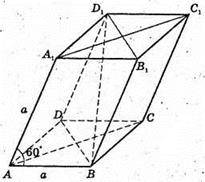
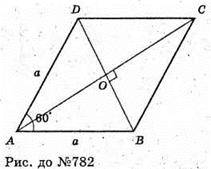
Нехай кожна грань паралелепіпеда – ромб зі стороною а і кутом 60°.
Діагоналі ромба: BD = АВ = AD = а; 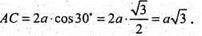
У паралелепіпеда чотири діагоналі: AC1; BD1; DB1; А1С;
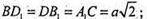
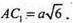
Відповідь: 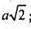
783.
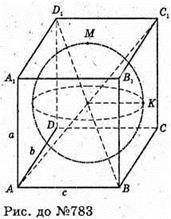
Нехай дано паралелепіпед ABCDA1B1C1D1 .
О – точка перетину діагоналей паралелепіпеда.
Сфера має центр О – у точці перетину його діагоналей,
Радіус сфери ОK = r; сума квадратів усіх ребер паралелепіпеда σ.
4a2 + 4b2 + 4с2 = σ.
Нехай М – будь-яка точка сфери.
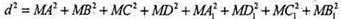 –
–
Сума квадратів відстаней від будь-якої точки сфери
До всіх вершин паралелепіпеда.