Перетворення подібності та його властивості. Гомотетія
УРОК № 38
Тема. Перетворення подібності та його властивості. Гомотетія
Мета уроку: формування понять перетворення подібності й гомотетії; вивчення властивостей перетворення подібності; формування вмінь застосовувати вивчені властивості й означення до розв’язування задач.
Тип уроку: комбінований.
Наочність і обладнання: таблиця “Перетворення подібності” [13].
Вимоги до рівня підготовки учнів: описують перетворення подібності й гомотетію; будують фігури, у які переходять дані фігури при перетвореннях подібності;
Хід уроку
І. Перевірка домашнього завдання
1. Перевірити наявність виконаних домашніх завдань та відповісти на запитання, які виникли в учнів під час їх виконання. 2. Фронтальна бесіда 1) Що називається паралельним перенесенням? 2) Сформулюйте основні властивості паралельного перенесення.
II. Самостійна робота
Самостійну роботу навчального характеру можна провести за посібником [14], тест 13 “Поворот і паралельне перенесення”.
III. Поетапне сприймання та усвідомлення нового
Поняття перетворення подібності й гомотетії
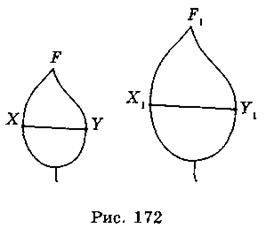
Перетворення фігури F на фігуру F1 називається перетворенням подібності, якщо при цьому перетворенні відстані між точками змінюються в ту саму кількість разів (рис. 172). Або іншими словами: якщо довільні точки X і Y фігури F при перетворенні подібності переходять у точки Х1 і Y1 фігури F1, то Х1Y1 = k? XY, де k – те саме число для будь-яких точок X і Y. Число k називається коефіцієнтом подібності. Якщо k = 1, то перетворення подібності є переміщенням.
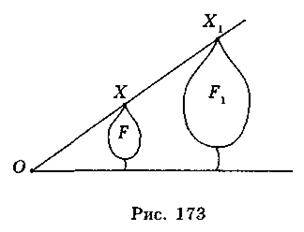
Нехай F – дана фігура і О – фіксована точка (рис. 173). Через довільну точку X фігури F проведемо промінь ОХ і відкладемо на ньому відрізок ОХ1, який дорівнює k? ОХ, де k – додатне число. Перетворення фігури F, при якому кожна її точка X переходить у точку Х1 і ОХ1 = k? OX, називається гомотетією відносно точки О; число k – коефіцієнтом гомотетії; фігури F і F1 – гомотетичними.
Властивості гомотетії
1) Гомотетія з коефіцієнтом k є перетворенням подібності з коефіцієнтом k. 2) При гомотетії пряма переходить у паралельну їй пряму або сама в себе; відрізок – у паралельний йому відрізок; кут – у рівний йому кут. 3) На координатній площині гомотетія точок А(х; у) і В(х1; у1) задається формулами: 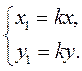
Властивості перетворення подібності
1) Перетворення подібності переводять прямі у прямі; промені – у промені; відрізки – у відрізки. 2) Кожна фігура подібна сама собі з коефіцієнтом подібності k = 1. 3) Перетворення подібності зберігає кути між променями.
Виконання вправ
1. Побудуйте фігуру, яка гомотетична заданому трикутнику ABC, прийнявши за центр гомотетії одну з його вершин, якщо коефіцієнт гомотетії дорівнює 2. 2. Побудуйте фігуру, яка гомотетична чотирикутнику ABCD при гомотетії з коефіцієнтом 0,5 і центром О – точкою перетину діагоналей. 3. При гомотетії точка X переходить у точку Х1, а точка Y – у точку Y1. Як знайти центр гомотетії, якщо точки X, Х1, Y, Y1 не лежать на одній прямій? 4. При гомотетії точка X переходить у точку Х1. Побудуйте центр гомотетії, якщо коефіцієнт гомотетії дорівнює 2.
IV. Закріплення й осмислення нового матеріалу
Розв’язування задач
1. Вершини трикутника ABC мають координати A(1; 1), В(-3; 5), С(-2; -3). Запишіть координати вершин трикутника, у який переходить трикутник ABC при гомотетії з коефіцієнтом 3 і центром у початку координат. 2. Запишіть рівняння кола, на яке відображається коло (х – 2)2 + (у + 2)2 = 16 при гомотетії з центром у початку координат і коефіцієнтом, який дорівнює:
А) 2; б) 0,5.
3. Запишіть рівняння прямої, яка гомотетична прямій у = 2х – 1 при гомотетії з центром у початку координат і коефіцієнтом, який дорівнює:
А) 3; б)  .
.
4. Доведіть властивості гомотетії. 5. Доведіть, що основи трапеції гомотетичні відносно точки перетину її діагоналей.
V. Домашнє завдання
1. Вивчити теоретичний матеріал. 2. Розв’язати задачі. 1) Гомотетія з центром у початку координат переводить точку А(3; -6) у точку В(1; -2). Знайдіть коефіцієнт гомотетії. 2) Запишіть рівняння кола, у яке переходить коло (x + 3)2 + (y – 3)2 = 9 при гомотетії з центром у початку координат і коефіцієнтом, який дорівнює:
А) 3; б)  .
.
3) Доведіть, що основи трапеції гомотетичні відносно точки перетину продовження її бічних сторін.
VI. Підбиття підсумків уроку
Запитання до класу
1. Що таке перетворення подібності? 2. Що таке гомотетія? центр гомотетії? коефіцієнт гомотетії? 3. Середня лінія MN трикутника ABC відтинає від нього гомотетичний трикутник MBN. Чому дорівнює коефіцієнт гомотетії?