Головна ⇒ 📌Довідник з геометрії ⇒ Перетворення в просторі – Декартові координати та вектори в просторі
Перетворення в просторі – Декартові координати та вектори в просторі
Геометрія
Декартові координати та вектори в просторі
Перетворення в просторі
Поняття перетворення для фігур у просторі означають так само, як і на площині (див. розділ “Геометрія. 8 клас”).
Рухом Називається перетворення, при якому зберігаються відстані між точками.
Властивості руху в просторі:
Прямі переходять у прямі, півпрямі – у півпрямі, відрізки – у відрізки, кути між півпрямими зберігаються, площина переходить у площину.
Зразки рухів у просторі:
Симетрія відносно точки; симетрія відносно прямої;
Приклад
Дана точка
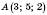 .
.Знайти точки, симетричні даній відносно координатних площин.
Відповідь: точка, симетрична точці А відносно Oху, – це
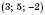 , відносно Oyz – це
, відносно Oyz – це 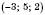 , відносно Oxz – це
, відносно Oxz – це 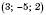 .
.Паралельним перенесенням у просторі називається таке перетворення, при якому довільна точка
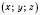 переходить у точку
переходить у точку 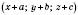 , де числа a, b, c – одні й ті самі для всіх точок
, де числа a, b, c – одні й ті самі для всіх точок 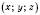 .
.У результаті паралельного перенесення точки зміщуються вздовж паралельних прямих (або прямих, що збігаються) на одну й ту саму відстань.
1. У результаті паралельного перенесення кожна пряма переходить у паралельну їй пряму (або в себе).
2. Які б не були точки А і
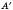 , існує єдине паралельне перенесення, у результаті якого точка А переходить у точку
, існує єдине паралельне перенесення, у результаті якого точка А переходить у точку 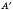 .
.3. У результаті паралельного перенесення в просторі кожна площина переходить або в себе, або в паралельну їй площину.
Related posts:
- Подібність просторових фігур – Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Подібність просторових фігур Перетворення фігури F називається Перетворенням подібності, якщо при цьому перетворенні відстані між точками змінюють себе в одну й ту саму кількість разів. Як і на площині, перетворення подібності в просторі переводить прямі у прямі, півпрямі у півпрямі, відрізки у відрізки і зберігає кути між півпрямими. […]...
- Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Візьмемо три взаємно перпендикулярні прямі Oх, Oy, Oz, які перетинаються в одній точці О (див. рисунок). Проведемо через кожну пару цих прямих площину. Площина, яка проходить через прямі Oх і Oу, називається площиною Oxy. Дві інші площини називаються відповідно Oxz і Oyz. Прямі Ox, Oy, Oz називаються Координатними […]...
- Паралельне перенесення в просторі Урок 49 Тема. Паралельне перенесення в просторі Мета уроку: формування знань учнів про паралельне перенесення в просторі; вивчення його властивостей та застосування їх до розв’язування задач. Обладнання: схеми “Відстань між двома точками” (див. урок 46) і “Координати середини відрізка” (див. урок 47), моделі куба і прямокутного паралелепіпеда. Хід уроку І. Перевірка домашнього завдання 1. Перевірити […]...
- Перетворення подібності та його властивості Урок 50 Тема. Перетворення подібності та його властивості Мета уроку: формування знань учнів про подібність просторових фігур, вивчення властивостей перетворення подібності та застосування їх до розв’язування задач. Обладнання: моделі куба і тетраедра. Хід уроку І. Перевірка домашнього завдання 1. Колективне обговорення контрольних запитань № 9-11 та розв’язування задач № 23-25 (1). 2. Математичний диктант. При […]...
- Декартові координати у просторі – СТЕРЕОМЕТРІЯ Формули й таблиці МАТЕМАТИКА СТЕРЕОМЕТРІЯ Декартові координати у просторі М – точка у просторі М(х, у, x) Мхy – проекція точки М на площину хоу; Мхy(х, о, у) Мх, Му, Mz – проекції точки М на осі OX, OY, OZ відповідно. Мх(х, о, о); Му(о, у, о); Мz(о, о, z). Відстань між точками А(x1,y1,z1) і […]...
- Перетворення симетрії в просторі. Симетрія в природі і на практиці Урок 47 Тема. Перетворення симетрії в просторі. Симетрія в природі і на практиці Мета уроку: формування знань учнів про перетворення симетрії в просторі та застосування знань до розв’язування задач. Обладнання: схема “Перетворення фігур”. Хід уроку І. Перевірка домашнього завдання 1. Усне коментування розв’язування домашніх завдань. 2. Математичний диктант. Дано трикутник АВС: Варіант 1 – А […]...
- Вектори в просторі – Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Вектори в просторі Усі основні означення векторів у просторі залишаються такими самими, як означення векторів на площині (див. розділ “Геометрія. 8 клас”). Координатами вектора , де , , називають числа, , . Вектори рівні тоді, й тільки тоді, коли вони мають відповідно рівні координати. Це дає підставу позначити […]...
- Паралельне перенесення УРОК № 37 Тема. Паралельне перенесення Мета уроку: формування поняття паралельного перенесення та вивчення властивостей паралельного перенесення; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення фігур. Рухи” [13]. Вимоги до рівня підготовки учнів: описують паралельне перенесення; будують фігури, у які переходять дані фігури при паралельному […]...
- Паралельне перенесення та його властивості Геометрія Рух Паралельне перенесення та його властивості Перетворення фігури F, при якому довільна її точка з координатами переходить у точку , де a і b – одні й ті самі для всіх точок, називається Паралельним перенесенням. Теорема. Паралельне перенесення є рухом. При паралельному перенесенні пряма переходить у паралельну пряму (або в себе) (див. рисунок). Існування […]...
- Поняття про рух, рівність фігур у просторі Урок 48 Тема. Поняття про рух, рівність фігур у просторі Мета уроку: формування понять: рух, рівні фігури. Доведення нової властивості руху: площина під час руху переходить у площину. Обладнання: схеми “Відстань між двома точками” (див. урок 46) і “Координати середини відрізка” (див. урок 48), модель куба. Хід уроку 1. Відповісти на запитання учнів, які виникли […]...
- Перетворення подібності та його властивості. Гомотетія УРОК № 38 Тема. Перетворення подібності та його властивості. Гомотетія Мета уроку: формування понять перетворення подібності й гомотетії; вивчення властивостей перетворення подібності; формування вмінь застосовувати вивчені властивості й означення до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення подібності” [13]. Вимоги до рівня підготовки учнів: описують перетворення подібності й гомотетію; будують фігури, у […]...
- Симетрія відносно прямої Геометрія Рух Симетрія відносно прямої Нехай а – фіксована пряма. Візьмемо довільну точку Х і опустимо перпендикуляр AX на пряму а. На продовженні цього перпендикуляра за точку А відкладемо відрізок . Точка називається Симетричною точці X відносно прямої А. Якщо точка X лежить на прямій а, то вона симетрична сама собі відносно прямої а. Очевидно, […]...
- Розміщення прямої і площини в просторі. Ознака паралельності прямої і площини Урок 13 Тема. Розміщення прямої і площини в просторі. Ознака паралельності прямої і площини Мета уроку: формування знань учнів про взаємне розміщення прямої і площини в просторі. Вивчення ознаки паралельності прямої і площини. Обладнання: стереометричний набір, моделі куба і тетраедра, схема “Аксіоми стереометрії”. Хід уроку І. Аналіз виконання тематичного оцінювання № 1. Зібрати зошити наприкінці […]...
- Координати і вектори у просторі 776. А(2; 0; 0), В(0; 0; 3), С(0; 5; -4), D(4; -3; 0), Е(2; 6; 4), F(6; -2; -6). 777. А(2; 0; 5), В(-4; 0; 2), С(4; 0; -2), D(1; 3; 1), A? хОz, В? xОz, C? xOz. Основа тетраедра ABC лежить у координатній площині хОz, Тому що yА = yB = yC = 0. […]...
- Перетворення простору 1. 1) Вектор паралельного перенесення, що переводить відрізок ОА в СВ: Вектор, що переводить відрізок ОС в АВ: 2) Вектор, що переводить ОС в АВ: Вектор, що переводить О А в СВ: 3) Вектор, що переводить ОС в АВ: Вектор, що переводить ОА в СВ: 4) Вектор, що переводить ОС в АВ: Вектор, що переводить […]...
- Симетрія відносно точки Геометрія Рух Симетрія відносно точки Нехай O – фіксована точка, X – довільна точка площини. Відкладемо на продовженні відрізка OX за точку O відрізок , що дорівнює OX. Точка називається Симетричною точці X відносно точки O (див. рисунок). Очевидно, що точка, симетрична , є точка X. Перетворення фігури F у фігуру , при якому кожна […]...
- Геометричні перетворення у просторі. Рухи 306. Пряма і площина відображуються на себе відносно будь-якої точки, що належить їм. 307. Два нерівні відрізки бути симетричними відносно деякої точки не можуть. 308. Відносно початку координат: Точці А(1; -3; 2) симетрична A1(-1; 3;-2); Точці В(-5; 0; 2) – B1(5; 0; -2); Точці С(3; -1; 0) – С1 (-3; 1; 0); Точці D(0; 0; […]...
- Властивості перетворення подібності Геометрія Подібність фігур Властивості перетворення подібності Теорема 1. Перетворення подібності переводить прямі у прямі, півпрямі – у півпрямі, відрізки – у відрізки. Теорема 2. Перетворення подібності зберігає кути між півпрямими. Із цього випливає, що перетворення подібності переводить паралельні прямі в паралельні прямі. Дві фігури називаються Подібними, якщо вони переводяться одна в одну перетворенням подібності. Позначення: […]...
- Вектори і координати 74. 1) 2) B i C, A i D; 3 ) 4 ) 75. 76. I – паралелограм. 77. – паралелограм 80. 1) 2) 3) 81. 1) 2 ) 3) 4) 82. 1) φ = 60°. 2) φ = 180°, cos 180° = -1. 3) φ = 42°. 4) φ = 17°12′. 83. α ≈ […]...
- Паралельне проектування та його властивості. Зображення просторових фігур на площині Урок 21 Тема. Паралельне проектування та його властивості. Зображення просторових фігур на площині Мета уроку: формування знань про паралельне проектування. Вивчення властивостей паралельного проектування. Дати уявлення про зображення просторових фігур на площині. Обладнання: стереометричний набір. Хід уроку І. Перевірка домашнього завдання 1. Відповісти на запитання, які виникли в учнів при розв’язуванні домашньої задачі. 2. Самостійна […]...
- Взаємне розміщення прямої та площини і площин у просторі. Перпендикуляр до площини. Взаємне розміщення площин у просторі УРОК № 53 Тема. Взаємне розміщення прямої та площини і площин у просторі. Перпендикуляр до площини. Взаємне розміщення площин у просторі Мета уроку: повторити, привести в систему й розширити відомості про площину та взаємне розміщення двох площин у просторі; ознайомити учнів з різними випадками взаємного розміщення прямої і площини; дати уявлення про перпендикуляр до площини. […]...
- Перпендикулярність прямих у просторі Урок 25 Тема. Перпендикулярність прямих у просторі Мета уроку: формування поняття про перпендикулярні прямі. Вивчення теореми про прямі, що перетинаються і паралельні двом перпендикулярним прямим. Обладнання: стереометричний набір. Хід уроку В кінці уроку збираються учнівські зошити для перевірки їх ведення та виконання домашнього завдання. III. Сприйняття й усвідомлення нового матеріалу Означення перпендикулярних прямих у просторі […]...
- Гомотетія і перетворення подібності 480. ΔABC і ΔA1B1С1 гомотетичні з центром Р, R = 2. 481. Тетраедр DA1B1С1 гомотетичний тетраедру DABC відносно т. D, R = 0,5. 482. Р і A симетричні відносно В. Тетраедр A1B1C1D1 гомотетичний тетраедру ABCD відносно т. Р із коефіцієнтом R = -1. 483. В результаті гомотетії відносно т. А т. О – центроїд грані […]...
- Взаємне розміщення прямих у просторі УРОК № 52 Тема. Взаємне розміщення прямих у просторі Мета уроку: повторити, привести в систему й розширити відомості про взаємне розміщення двох прямих у просторі. Тип уроку: комбінований. Наочність і обладнання: таблиця “Початкові відомості стереометрії” [13]. Вимоги до рівня підготовки учнів: описують взаємне розміщення в просторі двох прямих; застосовують вивчені означення та властивості до розв’язування […]...
- Вектори у просторі – ВЕКТОРИ Формули й таблиці МАТЕМАТИКА ВЕКТОРИ Вектори у просторі Вектор – спрямований відрізок А – початок вектора В – кінець вектора Модуль вектора – довжина відрізка, який зображує вектор: ||. Два вектори рівні, якщо вони однаково спрямовані і мають рівні модулі. Координати вектора з початком у точці А(x1,y1,z1) і кінцем у точці В(х2,у2,z2). Рівні вектори мають […]...
- Прямокутна система координату просторі Урок 44 Тема. Прямокутна система координату просторі Мета уроку: знайомство з декартовою прямокутною системою координат у просторі. Обладнання: модель куба. Хід уроку І. Аналіз виконання тематичного оцінювання II. Перевірка домашнього завдання В кінці уроку збираються учнівські зошити для перевірки їх ведення й виконання домашнього завдання. III. Сприйняття й усвідомлення нового матеріалу Прямокутна система координат на […]...
- Площина. Пряма. Промінь УРОК 11 Тема. Площина. Пряма. Промінь Мета: закріпити знання, здобуті на попередньому уроці, про властивості прямої, площини і променя; розвивати просторову уяву учнів; перевірити засвоєння матеріалу з тем “Відрізок” та “Площина. Пряма. Промінь” під час виконання самостійної роботи. Тип уроку: засвоєння навичок та вмінь. Хід уроку I. Перевірка домашнього завдання та актуалізація опорних знань Усні […]...
- Поняття про перетворення фігур УРОК № 32 Тема. Поняття про перетворення фігур Мета уроку: дати уявлення учням про перетворення фігур на площині. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення фігур. Рухи” [13]. Вимоги до рівня підготовки учнів: пояснює, що таке перетворення. Хід уроку І. Перевірка домашнього завдання Перевірити наявність виконаного домашнього завдання та відповісти на запитання, які виникли […]...
- Властивості руху Геометрія Рух Якщо кожну точку даної фігури змістити деяким чином, то дістанемо нову фігуру. Кажуть, що ця фігура утворюється перетворенням даної. Перетворення однієї фігури в іншу називається Рухом, якщо це перетворення зберігає відстань між точками. Властивості руху 1. Два рухи, виконані послідовно, дають знову рух. 2. Перетворення, обернене до руху, є рух. 3. Під час […]...
- Перпендикулярність прямих і площин Геометрія Стереометрія Перпендикулярність прямих і площин Дві прямі називаються Перпендикулярними, якщо вони перетинаються під прямим кутом. Теорема 1. Якщо дві прямі, які перетинаються, паралельні відповідно двом іншим перпендикулярним прямим, то інші прямі теж перпендикулярні. Теорема 2. Через будь-яку точку прямої у просторі можна провести безліч перпендикулярних до неї прямих (див. рисунок). (Усі прямі лежать у […]...