Вектори і координати
74.
1)
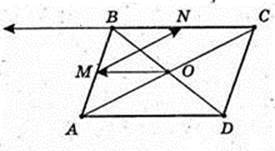
2) B i C, A i D;
3 ) 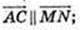
4 ) 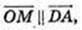
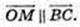
75.
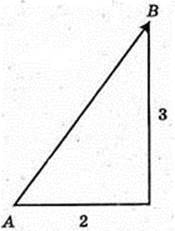
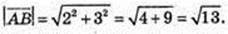
76.
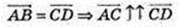 I
I 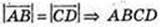 – паралелограм.
– паралелограм.
77.
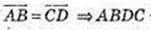 – паралелограм
– паралелограм 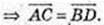
80.
1) 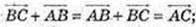
2) 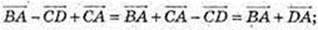
3) 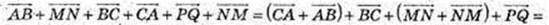
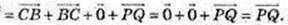
81.
1) 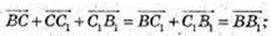
2
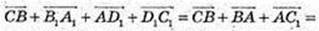
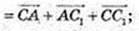
3) 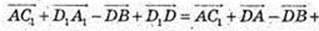
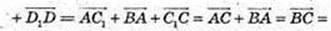
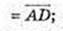
4) 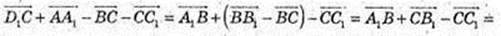
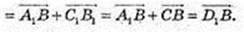
82.
1) 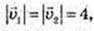 φ = 60°.
φ = 60°.
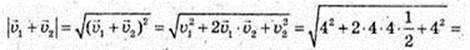
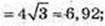
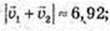
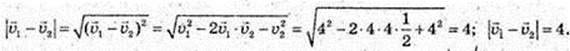
2) 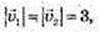 φ = 180°, cos 180° = -1.
φ = 180°, cos 180° = -1.


3) 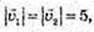 φ = 42°.
φ = 42°.
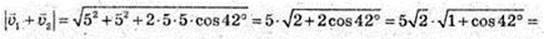
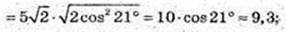
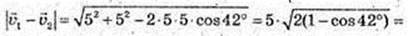
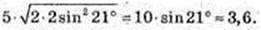
4)
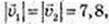 φ = 17°12′.
φ = 17°12′.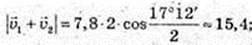
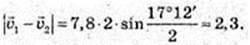
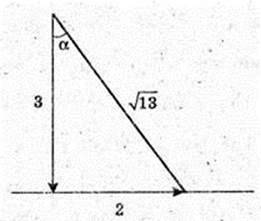
83.
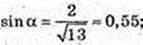 α ≈ 34°.
α ≈ 34°.
84.
1)
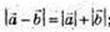
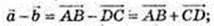
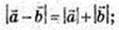
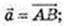
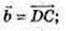
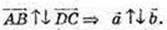
2)
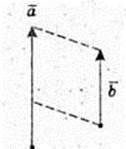
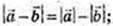
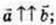
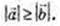
3)
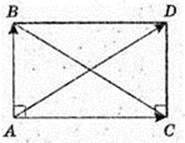
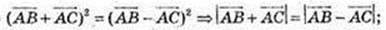
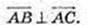
4)
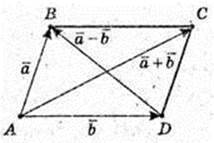
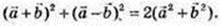
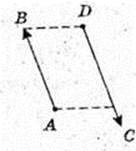
Сума квадратів діагоналей паралелограма дорівнює сумі квадратів всіх сторін паралелограма.
85.
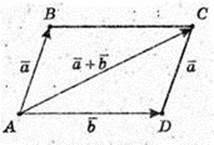
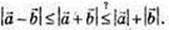
ΔАСD: довжина сторони AC не більше суми сторін AD i DC:
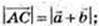
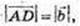
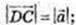
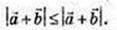
Довжина відрізка AC не менше різниці відрізків AD i DC:
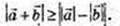
86.
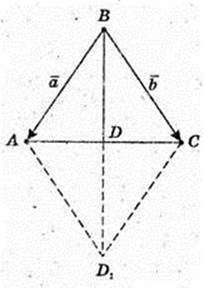
1) 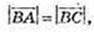
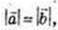
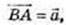
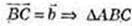 рівнобедрений, тоді
рівнобедрений, тоді 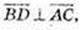
BD – медіана і 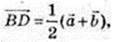
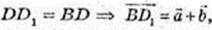
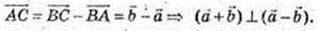
2) Нехай 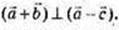 Тоді діагоналі паралелограма, побудованого на векторах
Тоді діагоналі паралелограма, побудованого на векторах
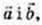 перпендикулярні. Отже це – ромб, в нього сторони рівні
перпендикулярні. Отже це – ромб, в нього сторони рівні 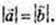
Інше доведення:
1. 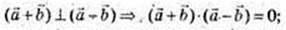
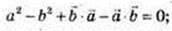
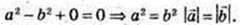
Маємо: 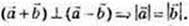
2. 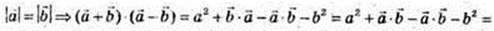
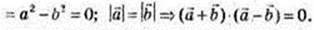
87.
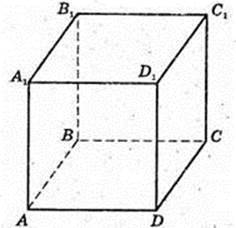
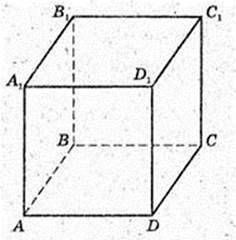
ABCDA1B1С1D1 – куб, AB = а.
1)
А) 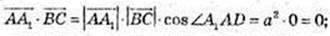
Б) 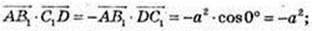
В) 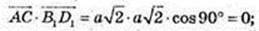
2) 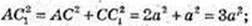
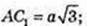
3 ) ∠ (AC1, CB1) = φ
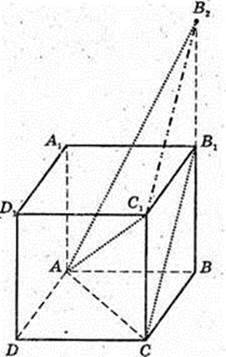
Додаткова побудова: продовжимо BB1 за точку B1 на відрізок, рівний BB1,
Де BB1 = α. ΔABB2: BB2= 2а, 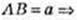
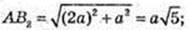
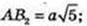
ΔAB2C1: 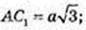
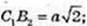
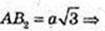
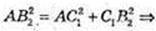
ΔAC1B2 = 90°.
Кут дорівнює 90°.
88.
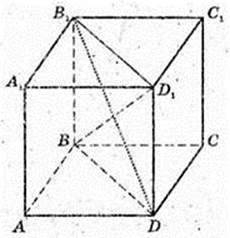
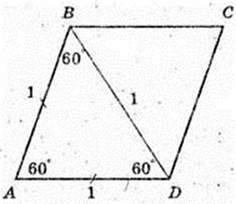
ABCDA1B1C1D1 – паралелепіпед. AB = AD = AA1 = 1. AA1 + (ABC), ∠BAD = 60°. DB -? φ = ∠ (DB1, BD) = ?
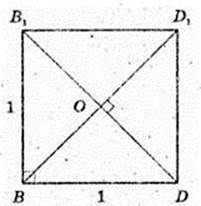
BB1D1D – квадрат. DB1 + BD1, ∠ DOD1 = 90°,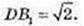
ABCD – ромб. BD =AD = AB = 1.
89.
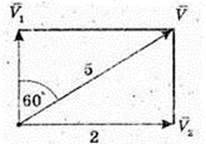
1) 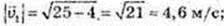
2) 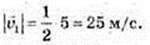
90.
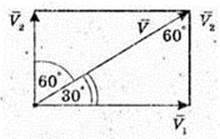
1) 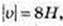
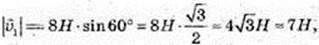
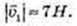
2) 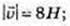 α = 22°, β = 570°.
α = 22°, β = 570°.
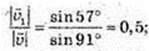
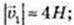
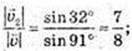
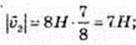
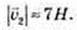
3) α = 26°, β= 146°.
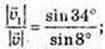
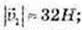
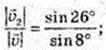
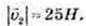
91. 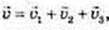 де
де 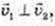
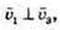
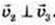
1) 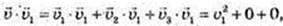
Де 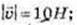
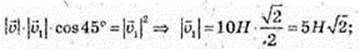
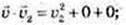
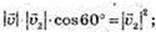
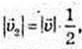
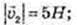
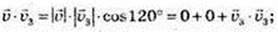
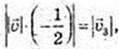
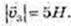
2) 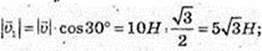
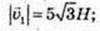
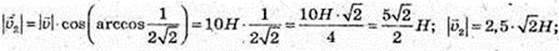
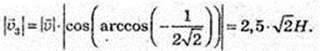
92.
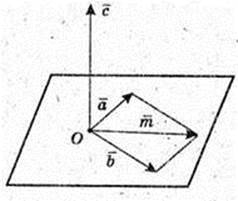
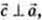
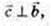
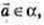

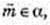
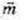 – довільний вектор площини α.
– довільний вектор площини α.
Довести: 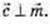
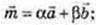
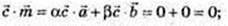
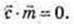
Доведено: якщо пряма перпендикулярна до двох прямих, що лежать у площині і проходять через точку перетину даної прямої з площиною, то ця пряма перпендикулярна до площини.
93.
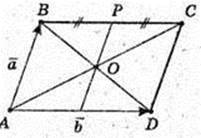
BP = PC.
1) 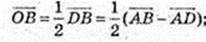
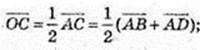
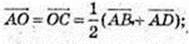
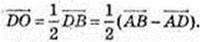
2) 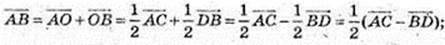
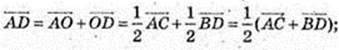
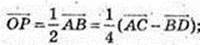
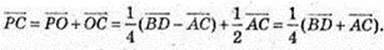
94.
M? DD1, DM = D1M; N? CC1, CN = C1N; P? BC1,
BP = PC1; 
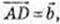
1) 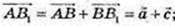
2) 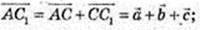
3) 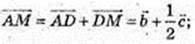
4) 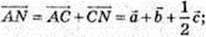
5) 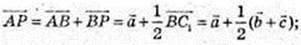
6) 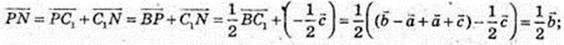
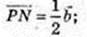
7) 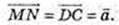
95.
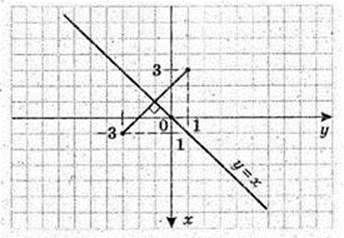
Α(1;-3).
1) А? IV;
2) -3;
3) 3;
4) 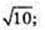
5) точка А1 симетрична точці А( 1; -.3) відносно осі Ох, А(1; 3).
Точка А2 симетрична точці А(1;-3) відносно осі Oy, А2(-1; -3).
Точка А31 симетрична точці А(1;-3) відносно точки О(0; 0; 0).
6) Точка В симетрична точці А(1; -3) відносно бісектриси третього квадрата,
В(- 3; 1).
96.
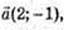
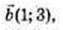
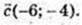
1) 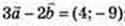
2) 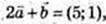
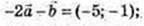
3) 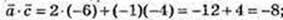
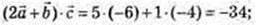
4) 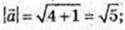
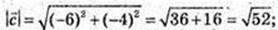
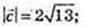
5) 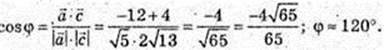
97.
A)
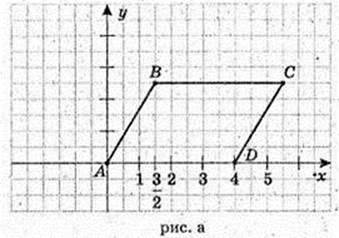
ABCD – паралелограм. ∠ DAB = 60°, AD = 4, AB = 3.
А(0; 0); 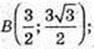
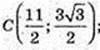 D(4; 0).
D(4; 0).
Б)
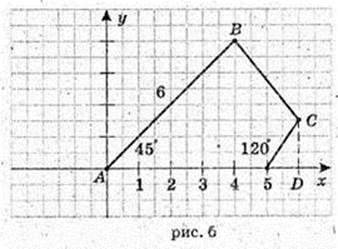
AB = 6, AD = 5, DC = 2, ∠ DAB = 45°, ∠ ADC = 120°.
А(0; 0); 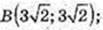
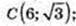 D(5; 0).
D(5; 0).
98.
А(-3; 1; 2).
1) ПрОх A = -3; ПрОy A = 1; ПрОх А = 2.
2) (-3; 1),(-3; 2),(1; 2);
3) 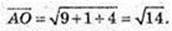 РА, хy = 2, РА, хz = 3.
РА, хy = 2, РА, хz = 3.
99.
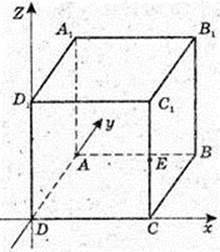
ABCDA1B1CiD1 – куб. DA = DC = DD1 = 1.
1) В(1; 1; 0), С( 1; 0; 0), C1(1; 0: 1);
2) CE = EC1, 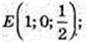
3) В1(1; 1; 1). Точка D найбільш віддалена від точки В.
4) M(1; 0; 5) зовні куба. 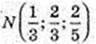 усередині куба.
усередині куба.
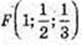 на поверхні куба.
на поверхні куба.
100.
Розглянемо всі точки координатного простору, у яких х = а, а – число, у і z – задовільні числа.
X = а незалежно від у і z. Всі такі точки простору знаходяться на відстані а від координатної площини уz, вони заповнюють площину, паралельну площині уz, або збігаються з площиною уz, якщо х = 0, а = 0.
101 .
A(-1;3; 1) 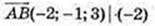
В(-3; 2; 4) 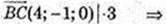
С( 1; 1; 4) 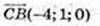
1) 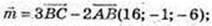
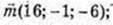
2) 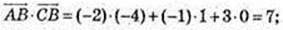
3) М(х; у; z) – ? 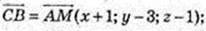
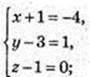
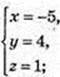 М(- 5; 4; 1).
М(- 5; 4; 1).
102.
А(1; -2; -1) 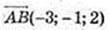
В(-2; 1; 1) 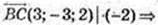
C(1; -2,-3) 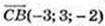
1) 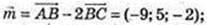
2) 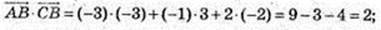
3) N(x; у; z) – ? 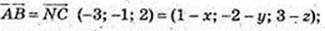
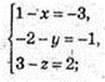
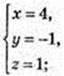 N(4; -1; 1).
N(4; -1; 1).
103.
А(-1; 3; 2), В(-2; 4; 0), М(1; 1; -3), N(0; 5; 0), Р(-3; 0; 2), Q(2; -1: 4):
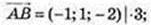
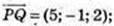
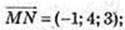
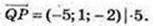
1) 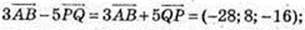
2) 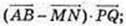
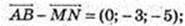
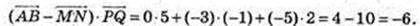
104.
А(5; 1;- 2)→В(6; 3; 3) 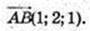
1) С(1; 0; 1), C 1 (x;y;z); 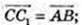
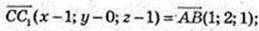
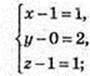

2) D(-3; 2; 1), D1(x; у; z); 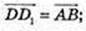
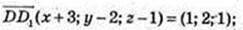
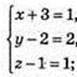
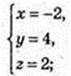 D1(-2; 4; 2).
D1(-2; 4; 2).
105.
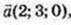
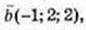
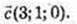
1) 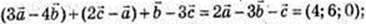
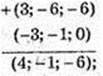
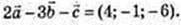
2) 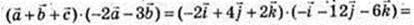
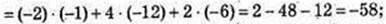
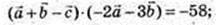
3) 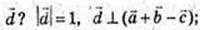
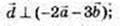
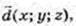
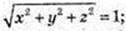
Х2 + у2 + z2= 1. 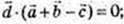
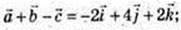 -2х + 4у + 2z = 0;
-2х + 4у + 2z = 0;
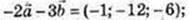 – x – 12у – 6z = 0;
– x – 12у – 6z = 0;
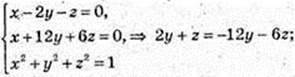
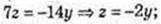
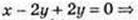
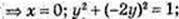
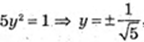
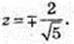 Або
Або
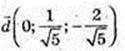
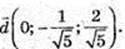
106.
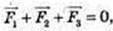
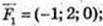
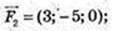
1) 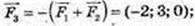
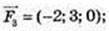
2) 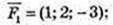
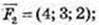
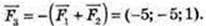
107.
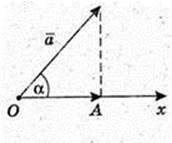
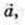
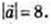
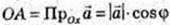
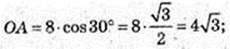
1) φ = 30°, 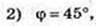
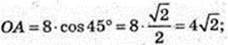
3) φ = 90°, OA = 8 × cos 90° = 0;
4) φ = 120°, OA = 8 × cos 120° = -4.
108.
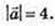
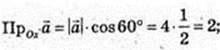
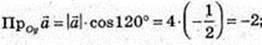
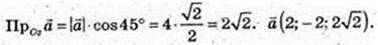
109. Паралелепіпед ABCDA1B1C1D1, А(3; 0,; 2), В(2; 4; 5),
А 1 (0; 3; 1), D1(7; 1; 2); 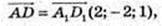
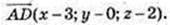 D(x;y; z).
D(x;y; z).
1) 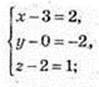
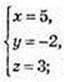 D(5; -2; 3);
D(5; -2; 3);
2) В1(х; у; z); 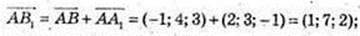
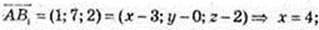
Y = 7; z = 4, В 1 (4; 7; 4).
3) С1(х; у; z); А(3; 0; 2).
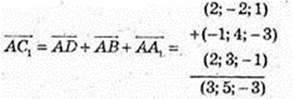
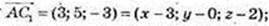
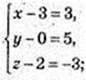
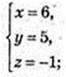 С 1 (6; 5; -1).
С 1 (6; 5; -1).
110.
А(4; 0; -3), В(8; 0; 1), С(2; 0; -1), D(-2; 0; 3);
1) 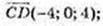
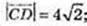
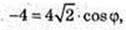
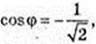 φ = 135°.
φ = 135°.
2) 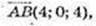
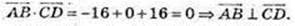
3) 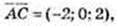
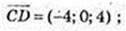
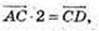
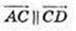
Колінеарні.
4) М(х; 0; 0). 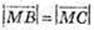 або
або 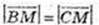
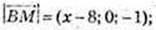
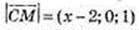
BM2 = CM2; (х – 8)2 + 02 + (-1)2 = (х – 2) + 02 + 12;
X2 – 16х + 64 + 1 = x2 – 4х + 4 + 1; 12х = 60; x = 5, M(5: 0; 0).
5) 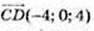
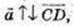
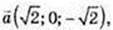
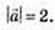
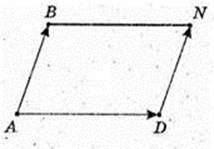
6) ABND – паралелограм. 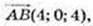
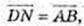 N(х; у; z).
N(х; у; z). 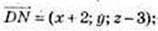
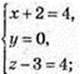
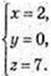 M(2; 0; 7).
M(2; 0; 7).
111.
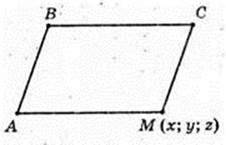
А(-2; 2; 0), В(0; 1; 1), C(4; 2; 0),D(1; 1; 1).
1) 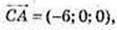
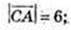
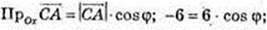
Cos φ = -1; φ = π; φ = 180°;
2) 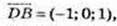
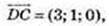
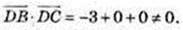
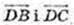 не є перпендикулярними.
не є перпендикулярними.
3) 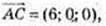
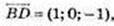
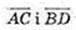
Не є колінеарними.
4) М(0; у·, 0), AM = CM, у – ?
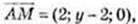
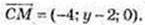
AM2 = CM2; 4 + (у – 2)2 = (-4)2 + (у – 2)2 неможливо.
На осі ординат не існує точки, рівновіддаленої від точок А і С,
5) 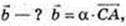
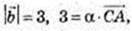
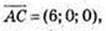
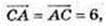
3 = α × 6, 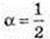
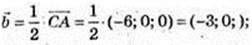
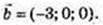
6) ABCM – паралелограм. 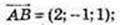
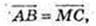
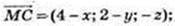
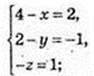
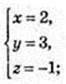 Μ(2; 3; -1).
Μ(2; 3; -1).
112.
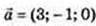
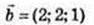
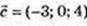
1) 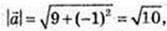
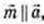
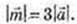
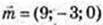 або
або 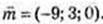
2) 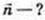
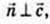 де
де 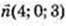
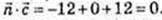
3) р – ?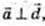 де
де 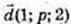
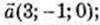
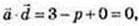 p = 3.
p = 3.
4) р – ? 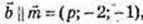
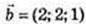
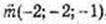 p = -2·
p = -2·
113.
1) A(-3; 1), В(1; 3), С(2; 1), D(-2; -1);
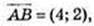
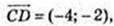
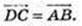
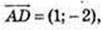
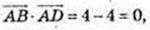
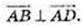
ABCD – паралелограм, ABCD – прямокутник.
2) А(-1: 2; 4), В(1; 0; 2), С(2; -3; 0), D(0; -1; 2);
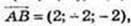
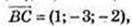
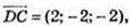
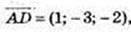
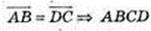 – паралелограм.
– паралелограм.
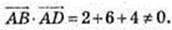
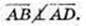
114.
А(1; -1; 1), В(1; 3; 1), С(4; 3; 1), D(4; -1; 1);
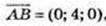
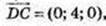
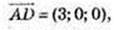
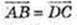
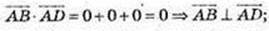
ABCD – прямокутник.
115.
Сфера (х + 3)2 + у2 + (z – 1)2 = 16.
1) А(-3; 1; 5), 02+ 12 + 42 ≠ 16.Точка А не лежить на сфері.
2) Центр сфери С(-3; 0; 1). В(-5; 2; 0),
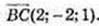
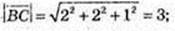
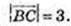
3) (х + 5) + (y – 2)2 + z2 = 16.
4) C1 симетрична точці С(-3; 0; 1) відносно площини yz.
С1(3; 0; 1). (х – 3)2 + у2 + (z – 1)2 = 16.
116.
Х2 + (y + z) + (z – 3)2 = 16.
1) A(0; -2; 7); 0 + (-2 + 2)2 + (7 – 3)2 = 16. Точка А лежить на сфері.
2) Центр сфери С(0: -2; 3), M(1; 0; -2).
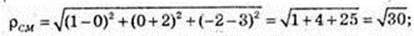
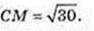
3) x2 + (у + 2)2 + (z – 3)2 = 9.
4) z2 + (y + 2)2 + (z + 3)2 = 16.
117.
α: 3x + 4y – z = 1. A(1; -1; 2), B(2; 3; -5), C(-1; 3; -2).
1) 3 × 1 + 4 × (-1) – 2 = -3; -3 ≠ 1. Точка не лежить з площині α.
2) 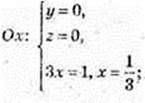
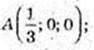
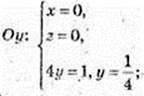
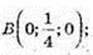
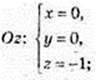 С(0; 0; -1).
С(0; 0; -1). 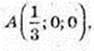
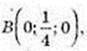 С(0; 0; -1).
С(0; 0; -1).
3) B(2; 3; -5), 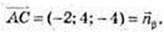
β: -2x + 4y – 4z + k = 0, k – ?
B? β → -2 × 2 + 4 × 3 – 4 × (-5) + k = 0; k = -28;
β: -2x + 4y – 4z – 80 = 0 | : (-2); x – 2y + 2z + 14 = 0;
4) α та β перетинаються.
5) 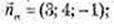
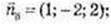
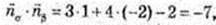
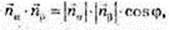
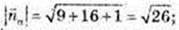
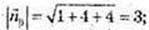
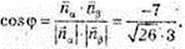
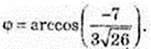
118.
α: x – 2y + 3z = 2. А(2;-1; 3), B(1; 0; -1), C(-1; 2; 1).
1) -1-2 × 2 + 3 × 1 = -2. Точка C не лежить в площині α.
2) 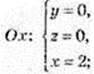 A(2; 0; 0);
A(2; 0; 0); 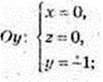 B(0; -1; 0);
B(0; -1; 0); 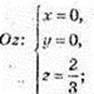
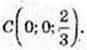
3) 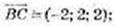
β: -2x + 2y + 2z + m = 0; – 2 × 2 + 2 × (-1) + 2 × З + m = 0, m = 0;
β: -2x + 2у + 2x = 0 | : (-2);
β: x – y – z = 0.
4) 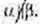 Площини а і β перетинаються.
Площини а і β перетинаються.
5) 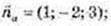
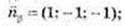
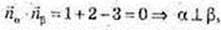
Кут між площинами α ? β дорівнює 90°.
119.
α: A × x + B × y + C × z + D = 0. Α(a; 0; 0), B(0; b; 0), С(0; 0; с).
A – ? В – ? C – ? D – ?
А × a + D= 0; 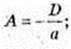 B × b + D = 0;
B × b + D = 0; 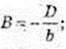
C × c + D = 0; 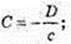
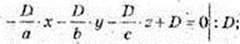
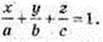
120.
X = t2*+1.
1) t? [1; 1,1]. x2 = (1,1)2 + 1; x1 = 12 + 1.
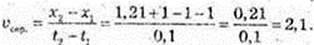
T? [1; 1,01]. x2 = (1,01)2 + 1; t2 = 1,01; x1 = 12 + 1; t1, = 1.
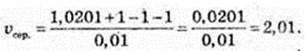
T? є [I; 1,001]. t2 = 1,001; t1 = 1; x2 = (1,001)2 + 1; х 1 = 12 + 1.
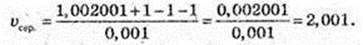
2) v = x’ = 2t, v(1) = 2.
121.
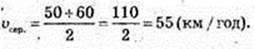
122.
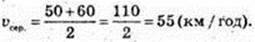
123.
X = 5t + 1, v1′ = 5; х =7t – 3, v2′ = 7; 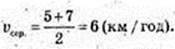
124. 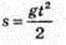
1) 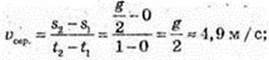
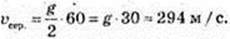
2) v = s’ = gt. v(1) = g, v(1) = 9,8 м/с; v(10)= 10g, v(10) = 98 м/с.
126.
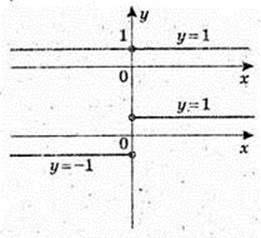
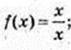
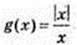
Функція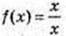 не існує в точці х = 0.
не існує в точці х = 0.
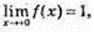
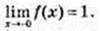
Функція 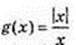 не існує в точці х = 0.
не існує в точці х = 0.