Подібність трикутників за двома кутами
Урок № 28
Тема. Подібність трикутників за двома кутами
Мета: домогтися розуміння учнями змісту першої ознаки подібності трикутників та наслідку з неї, плану їх доведення. Формувати вміння:
– відтворювати зміст вивченої ознаки та наслідку з неї;
– виділяти у трикутниках елементи для визначення їх подібності за двома кутами;
– застосовувати формулювання першої ознаки подібності трикутників до розв’язування задач.
Тип уроку: засвоєння нових знань.
Наочність та обладнання: конспект “Подібність трикутників”.
Хід
I. Організаційний етап
II. Перевірка домашнього завдання
Під час усного обговорення контрольних моментів задач домашньої роботи учні мають відтворити аргументовані міркування з використанням означення й властивостей подібних трикутників та їх лінійних елементів.
III. Формулювання мети і завдань уроку
З метою створення відповідної мотивації навчальної діяльності учнів пропонуємо їм відповісти на низку запитань.
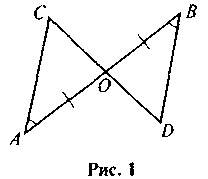
1. Які два трикутники називаються рівними? Чи можна довести, використовуючи означення рівних трикутників, що трикутники, зображені на рис. 1, є рівними? Яке твердження
2. Які два трикутники називаються подібними? Чи можна довести, використовуючи означення подібних трикутників, що трикутники, зображені на рис. 2, є подібними? Чи відомо вам твердження, яке можна було б для цього використати?
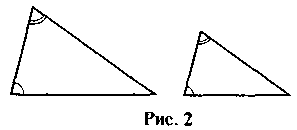
Відповіді на запитання допомагають учням усвідомити, що: по-перше, так само як і означення рівності трикутників, означення подібності трикутників має певні обмеження під час застосування; по-друге, зважаючи на існування певних аналогій між поняттями рівності та подібності трикутників та на існування ознак рівності трикутників, можна припустити, що є ознаки подібності трикутників, тобто твердження, що за обмеженої кількості даних елементів трикутників дозволяють установити подібність трикутників.
Отже, вивчення ознак подібності трикутників є загальною метою наступних трьох уроків. На цьому уроці (див. запитання вище) має бути встановлено, чи можна стверджувати, що трикутники подібні тільки за двома кутами, і в разі позитивної відповіді слід оволодіти вміннями використовувати цю ознаку для розв’язування задач.
IV. Актуалізація опорних знань
З метою успішного засвоєння учнями ознак подібності трикутників за двома кутами, а також ідеї її доведення, учням слід активізувати знання і вміння щодо теореми про суму кутів трикутника; ознак рівності трикутників; властивостей кутів при паралельних прямих та січній; застосування теореми про пропорційні відрізки.
Виконання усних вправ за готовими рисунками
1 |
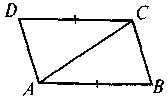
| Дано: AB || CD, AB = CD. Довести: ?ABC = ?CDA |
2 |
| Дано: AB || CD, AB = CD. Довести: |
3 |
| Дано: AD || BC, AO = OB. Довести: CO = OD |
|
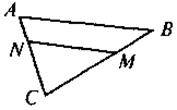
| Дано: АВ = ВС, MN || АВ. Довести: MN = МС |
5 |
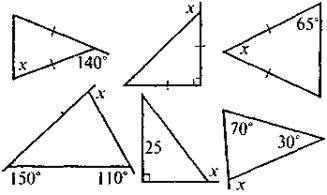
| На кожному з наведених рисунків знайдіть міру кута х |
V. Засвоєння знань
План вивчення нового матеріалу
1. Теорема (ознака подібності трикутників за двома кутами): формулювання та доведення.
2. Наслідки з теореми: формулювання і доведення.
3. Перша ознака подібності для окремих видів трикутників.
@ З огляду на суттєву відмінність програми з математики для дванадцятирічної школи від “старої” програми (див. методичний коментарію уроку № 26), доведення ознаки подібності трикутників за двома кутами ведеться не через виконання перетворення подібності (як це було раніше), а здійснюється з посиланням на теорему про суму кутів трикутника, властивості відповідних кутів при паралельних прямих і січній, другу ознаку рівності трикутників та теорему про пропорційні відрізки. Отже, якщо на попередньому етапі уроку належним чином було проведено підготовчу роботу, то доведення ознаки подібності трикутників за двома кутами має бути зрозумілим для учнів, а тому відтворення доведення (як не вимагає програма) не становитиме для них труднощів. З метою полегшення запам’ятовування доведення доцільно скласти план, який згодом учні зафіксують у зошитах. Закріплення змісту доведеної теореми проводиться під час виконання усних вправ (див. нижче).
Крім теореми, що виражає ознаку подібності трикутників за двома кутами, автор вважає за доцільне на цьому уроці розглянути деякі опорні факти (безпосередньо випливають із доведеної ознаки), які мають досить велике практичне значення. Мова йде про такі твердження:
– пряма, що перетинає дві сторони трикутника і проходить паралельно до третьої сторони, відтинає від даного трикутника подібний до нього трикутник;
– трикутники, утворені основами трапеції і прилеглими до них відрізками діагоналей, на які вони діляться точкою свого перетину, подібні (див. рис. 3).
ABCD – трапеція (BC || AD); О – точка перетину діагоналей, ?AOD ~ ?СОВ.
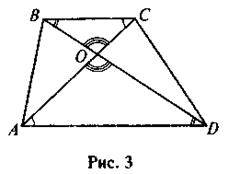
Справедливість першого твердження очевидна (див. підручник); для доведення другого твердження достатньо пригадати означення трапеції (основи паралельні) та властивість внутрішніх різносторонніх кутів при паралельних прямих та січній. Попереджаючи можливі типові помилки у застосуванні другого наслідку (для трапеції), вчитель має одразу звернути увагу учнів на те, що різні відповідні вершини подібних трикутників трапеції є кінцями однієї і тієї самої діагоналі. Що стосується трансформації ознаки для окремих видів трикутників (усі рівносторонні трикутники подібні; рівнобедрені трикутники подібні, якщо мають або по рівному куту між бічними сторонами, або по рівному куту при основі), то ці твердження можна довести під час вивчення нового матеріалу, спираючись на доведену ознаку для довільного трикутника, або розв’язати відповідні завдання, після чого узагальнити здобуті відповіді.
VI. Формування первинних умінь
Виконання графічних вправ
1. Накресліть трапецію і проведіть її діагоналі.
А) Виділіть кольором подібні трикутники, які утворилися на рисунку. За якою ознакою можна довести їх подібність?
Б) Виміряйте довжини відрізків однієї діагоналі, на які вона ділиться точкою перетину діагоналей. Виміряйте довжину однієї з основ трапеції і обчисліть довжину другої основи, користуючись подібністю трикутників. Перевірте результат вимірюванням.
2. Накресліть трикутник і проведіть пряму, яка паралельна одній із його сторін і перетинає дві інші сторони.
А) Виділіть кольором подібні трикутники, які утворилися на рисунку. За якою ознакою можна довести їх подібність?
Б) Виміряйте кути, під яким дана пряма перетинає сторони трикутника, і знайдіть усі кути трикутника.
Виконання письмових вправ
1. На рисунку 4 знайдіть подібні трикутники і доведіть їх подібність.
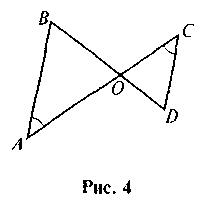
2. За даними рисунка 5 доведіть подібність трикутників ABC і А1В1С1.
3. Продовження бічних сторін АВ і CD трапеції ABCD перетинаються в точці О.
А) Доведіть, що? AOD ~ ?ВОС.
Б) Знайдіть AD, якщо ВС = 4 см. ОВ = 6 см, ОА = 9 см.
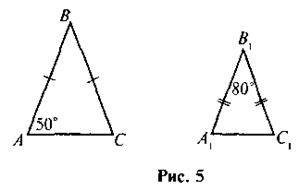
4. Два рівнобедрені трикутники мають рівні куги при основі. Основа одного трикутника дорівнює 8 см, а бічна сторона – 6 см. Знайдіть периметр другого трикутника, якщо його основа дорівнює 4 см.
5. Доведіть, що будь-які два рівнобедрені прямокутні трикутники подібні.
@ Під час розв’язування задач (починаючи вже з усних вправ) слід вимагати від учнів побудови доведення у формі, яка їм знайома із сьомого класу (застосовувалась під час виконання доведення рівності трикутників).
Розглянемо трикутники… і… У них:
(дається перелік пар відповідно рівних кутів трикутників з обгрунтуванням відповідно до ознаки подібності або відповідно до певного наслідку), тому трикутники… і… подібні за двома кутами (або як рівнобедрені…)
VII. Підсумки уроку
Чи можуть бути подібними:
А) прямокутний і рівнобедрений трикутники;
Б) прямокутний і рівносторонній трикутники;
В) трикутник із кутом 50° і трикутник із кутом 100°;
Г) трикутник із кутом 60° і трикутник із кутом 120°?
VIII. Домашнє завдання
Вивчити зміст за доведення першої ознаки подібності трикутників.
Розв’язати задачі.
1. На рисунку 6 знайдіть подібні трикутники і доведіть їх подібність.
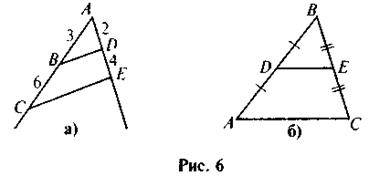
2. Діагоналі трапеції ABCD (AD || BC) перетинаються в точці О.
А) Доведіть, що? AOD ~ ?СОВ.
Б) Знайдіть ВС, якщо AD = 16 см, АО : ОС = 4 : 3.
3. Визначте, чи побідні трикутники зі сторонами:
А) 3, 4, 6 і 9, 15, 18;
Б) 2, 3, 3 і 8, 12, 12.
4. Два рівнобедрені трикутники мають рівні кути, протилежні до основи. Периметри цих трикутників дорівнюють відповідно 15 см і 10 см. Знайдіть сторони другого трикутника, якаю бічна сторона першого трикутника дорівнює 6 см.
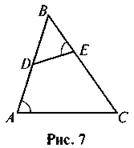
5. На рисунку 7 знайдіть подібні трикутники і доведіть їх подібність.
 A =
A = 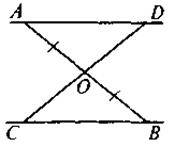
 4
4