Поняття про рух, рівність фігур у просторі
Урок 48
Тема. Поняття про рух, рівність фігур у просторі
Мета уроку: формування понять: рух, рівні фігури. Доведення нової властивості руху: площина під час руху переходить у площину.
Обладнання: схеми “Відстань між двома точками” (див. урок 46) і “Координати середини відрізка” (див. урок 48), модель куба.
Хід уроку
1. Відповісти на запитання учнів, які виникли в процесі розв’язування задач № 16, 18.
2. Математичний диктант.
Куб ABCDKLMN розташовано в системі координат:
Варіант 1 – рис. 264; варіант 2 – рис. 256, діагональ
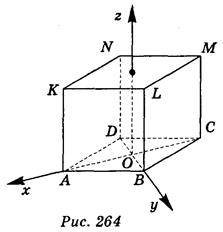
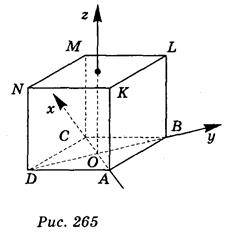
Запишіть координати точки, яка симетрична:
1) точці А відносно точки О; (2 бали)
2) точці L відносно осі z; (2 бали)
3) точці N відносно площини ху; (2 бали)
4) точці К відносно площини уz; (2 бали)
5) точці М відносно точки О; (2 бали)
6) точці О відносно точки К. (2 бали)
Відповідь. Варіант 1. 1) C(-1; 0; 0); 2) N(0; -1;  ); 3) (0;-1;-
); 3) (0;-1;- );4) М(-1;0;
);4) М(-1;0; ); 5) (1;0;-
); 5) (1;0;- ); 6) (2;0;2
); 6) (2;0;2 ).
).
Варіант 2. 1) C(1;0;0); 2) N (0; -1;  ); 3) (0;-1;-
); 3) (0;-1;-
 ); 5) (-1;0;-
); 5) (-1;0;- ); 6) (-2;0;2
); 6) (-2;0;2 ).
).Рухом у просторі називається перетворення, при якому зберігаються відстані між точками. Доведемо загальні властивості рухів.
Теорема 1.
Точки, які лежать на прямій, під час руху переходять у точки, які лежать на прямій, і зберігається порядок їх взаємного розміщення.
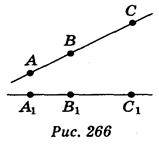
Нехай точки А, В, С лежать на прямій, причому точка В – між точками А і С, тобто АВ + ВС = АС (рис. 266). Якщо рух відображає дані точки на точки А1, В1, С1, то А1В1 = АВ, А1C1 = АС, В1С1 = ВС, тобто має місце рівність А1B1 + В1С1 = А1С1. А це означає, що точка В1 лежить між точками А1 і С1. Теорему доведено.
Наслідок. Рух відображає пряму на пряму, промінь – на промінь, відрізок – на відрізок, що дорівнює даному.
Теорема 2.
Рух відображає трикутник на трикутник, що дорівнює даному.
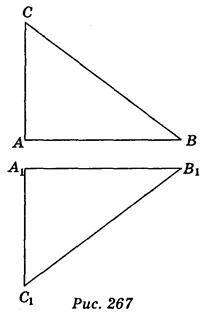
Нехай дано довільний трикутник АВС (рис. 267). Рух відображає його сторони АВ, ВС, АС на відрізки А1B1, В1С1, А1С1, причому A1B1 = АВ, В1С1 = ВС, А1С1 = АС, отже, ?А1В1С1 = ?АВС. Теорему доведено.
Наступна теорема характеризує нову властивість руху в просторі.
Теорема 3.
Рух відображає площину на площину.
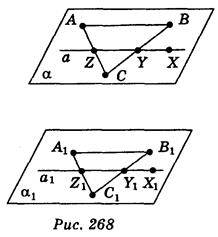
Нехай? – довільна площина (рис. 268), візьмемо на ній будь-які точки А, В, С, що не лежать на одній прямій. Під час руху точки А, В, С перейдуть у точки А1, B1, С1, які не лежать на одній прямій. Проведемо через точки А1, B1, С1 площину?1. Доведемо, що під час руху? переходить у площину?1. Нехай X – довільна точка?. Проведемо через неї у площині? пряму а, яка перетинає трикутник АВС у двох точках Z і Y. Пряма а перейде в деяку пряму а1. Точки Y, Z прямої а перейдуть у точки Z1, Y1, які належать трикутнику А1В1С1, а тому і площині?1. Отже, пряма а1 лежить у площині?1. Точка Х під час руху переходить у точку X1 прямої a1, а тому і площини?1. Теорему доведено.
Дві фігури називаються рівними, якщо вони суміщаються рухом.
1. Наведіть приклади рухів.
2. Дано два рівні відрізки із спільним кінцем. Якими рухами один із них можна відобразити на другий?
3. Задача № 20* із підручника (с. 55).
4. Наведіть приклади рівних фігур з оточення.
5. Дано два рівні куби із спільною гранню. Якими рухами їх можна сумістити?
6. Задача № 21 із підручника (с. 55).
III. Домашнє завдання
§4, п. 28; контрольні запитання № 6-8; задача № 19 (с. 55).
IV. Підведення підсумку уроку Запитання до класу
1) Яке перетворення фігури називається рухом?
2) В яку фігуру під час руху переходить площина?
3) Які фігури у просторі називаються рівними?