Порівняння радикалів
УРОК 35
Тема. Порівняння радикалів
Мета уроку. Формування умінь учнів порівнювати радикали.
І. Перевірка домашнього завдання
1. Фронтальна бесіда за № 25-37 із “Запитання і завдання для повторення” до розділу III.
2. Самостійна робота.
Варіант 1
1. Знайдіть область визначення виразу: а) 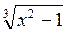 ; б)
; б) 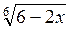 . (3 бали)
. (3 бали)
2. Обчисліть: а) 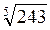 ; б) 5
; б) 5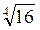 ; в)
; в) 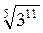 –
–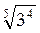 . (3 бали)
. (3 бали)
3. Спростіть: а) 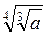 ; б)
; б)
4. Чи подібні радикали 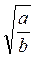 і
і 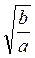 ? (3 бали)
? (3 бали)
1. Знайдіть область визначення виразу: а) 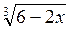 ; б)
; б) 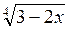 . (3 бали)
. (3 бали)
2. Обчисліть: а) 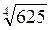 ; б) 4
; б) 4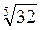 ; в)
; в) 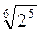 –
–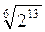 . (3 бали)
. (3 бали)
3. Спростіть: а) 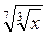 ; б)
; б) 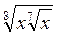 , х > 0. (3 бали)
, х > 0. (3 бали)
4. Чи подібні радикали 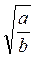 і
і 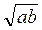 ? (3 бали)
? (3 бали)
Відповідь:
В-1: 1. а) R; б) x 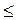 3. 2. а) 3; б) 10; в) 27. 3. а)
3. 2. а) 3; б) 10; в) 27. 3. а) 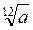 ; б)
; б) 
В-2: 1. а) R; б) х 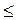 1,5. 2. а) 5; б) 8; в) 8. 3. а)
1,5. 2. а) 5; б) 8; в) 8. 3. а) 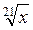 ; б)
; б) 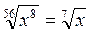 . 4. Подібні.
. 4. Подібні.
II. Сприймання і усвідомлення матеріалу про порівняння радикалів
Для порівняння радикалів застосовується теорема:
Теорема: Якщо а > b  0, то
0, то 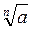 >
> 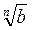 , тобто більшому додатному підкореневому виразу відповідає і більше значення кореня.
, тобто більшому додатному підкореневому виразу відповідає і більше значення кореня.
Проведемо доведення методом від супротивного. Припустимо, 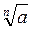 <
< 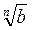 . Тоді за властивістю степенів з натуральним показником маємо
. Тоді за властивістю степенів з натуральним показником маємо 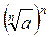 <
< 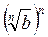 , тобто а < b. А це суперечить умові а > b.
, тобто а < b. А це суперечить умові а > b.
Приклад. Порівняємо числа 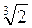 і
і 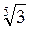 .
.
Подамо 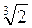 і
і 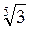 у вигляді коренів з одним і тим самим показником:
у вигляді коренів з одним і тим самим показником:
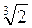 =
= 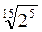 =
= 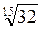 , а
, а 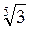 =
= 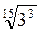 =
= 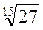 . Згідно з доведеною теоремою, так як 32 > 27, то
. Згідно з доведеною теоремою, так як 32 > 27, то 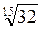 >
> 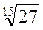 , а отже,
, а отже, 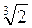 >
> 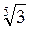 .
.
1. Порівняйте числа: а) 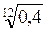 і
і 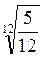 ; б)
; б) 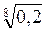 і
і 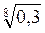 ; в)
; в) 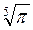 і
і 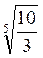 ; г)
; г) 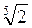 і
і 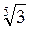 .
.
Відповідь: а) 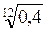 <
< 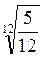 ; б)
; б) 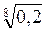 <
< 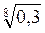 ; в)
; в) 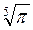 <
< 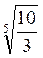 ; г)
; г) 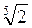 <
< 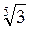 .
.
2. Що більше: а) 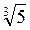 чи
чи 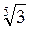 ; б)
; б) 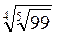 чи
чи 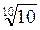 ; в)
; в) 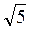 чи
чи 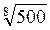 ; г)
; г) 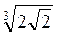 чи
чи  ?
?
Відповідь: а) 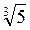 ; б)
; б) 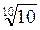 ; в)
; в) 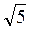 ; г)
; г) 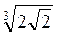 =
=  ?
?
3. Що менше: а) 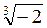 чи
чи 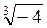 ; б)
; б) 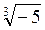 чи
чи 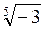 ?
?
Відповідь: а) 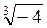 ; б)
; б) 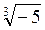 .
.
Безпосередньо з доведеної теореми випливає:
1) Якщо а > 1, то 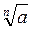 > 1 і
> 1 і 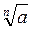 < а.
< а.
2) Якщо 0 < а < 1, то 0 < 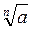 < 1 і
< 1 і 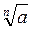 > а.
> а.
3) 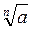 +
+ 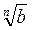 >
> 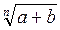 , при умові а > b
, при умові а > b  0, або b > а
0, або b > а  0.
0.
1. Визначте знак виразу: а) 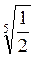 – 1 ; б)
– 1 ; б) 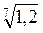 – 1; в)
– 1; в) 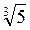 – 5; г)
– 5; г) 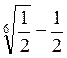 .
.
Відповідь: а) – ; б) + ; в) – ; г) +.
2. Розташуйте в порядку зростання: а)  ;
; 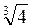 ;
; 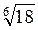 ; б)
; б) 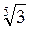 ;
; 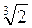 ;
; 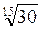 ; в)
; в) 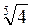 ;
; 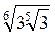 ;
; 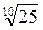 .
.
Відповідь: а) 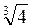 ;
; 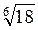 ;
;  ; б)
; б) 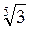 ;
; 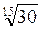 ;
; 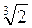 ; в)
; в) 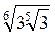 ;
; 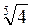 ;
; 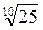 .
.
III. Підведення підсумків уроку
IV. Домашнє завдання
Запитання і завдання для повторення до розділу ІІІ № 13-15, 47. Вправи № 22, 26, 38.