Порівняння сторін і кутів трикутника
Урок № 37
Тема. Порівняння сторін і кутів трикутника
Мета: перевірити рівень засвоєння навчального матеріалу теми “Прямокутні трикутники”; домогтися засвоєння учнями змісту та схеми доведення теореми про співвідношення між сторонами і кутами трикутника; сформувати вміння відтворювати формулювання теореми про співвідношення між сторонами і кутами трикутника та використовувати це співвідношення під час розв’язування задач.
Тип уроку: засвоєння знань, умінь та навичок.
Наочність і обладнання: набір демонстраційного
ХІД УРОКУ
I. Організаційний момент
II. Перевірка домашнього завдання
Зібрати зошити з домашнім завданням та виконаною самостійною роботою.
Самостійна робота
Варіант 1
Початковий рівень
1. Знайдіть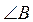 
(рис. 1).
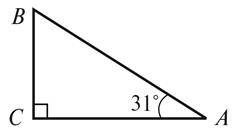
Достатній рівень
2. Дано:CD = 6 см. Знайдіть AB (рис. 2).
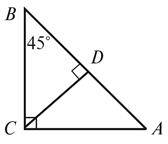
Високий рівень
3. Дано: AD – бісектриса кута BAC. Доведіть, що BD = CD (рис. 3).
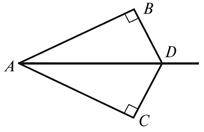
4. Кути 1, 2 і 3 – зовнішні кути трикутника
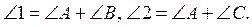Порівняйте кути A, B і C, якщо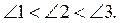 
Варіант 2
Початковий рівень
1. Знайдіть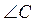 
(рис. 4).
Достатній рівень
2. Дано: AB =14 см. Знайдіть CD (рис. 5).
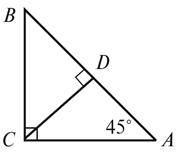
Високий рівень
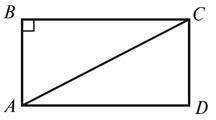
3. Дано: AB||CD.
Доведіть, що BC = AD (рис. 6).
4. Кути 1, 2 і 3 – зовнішні кути трикутника ABC, причому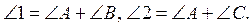 
Порівняйте кути A, B і C, якщо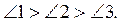 
ІІІ. Мотивація навчальної діяльності учнів. Формулювання мети уроку
Для того щоб учні усвідомили необхідність вивчення питання уроку, можна запропонувати до розв’язання задачу.
Задача. У прямокутному трикутнику найбільша сторона дорівнює 10 см. Знайдіть найменшу сторону, якщо гострі кути цього трикутника відносяться як 1 : 2.
Аналізуючи умову задачі, учні доходять висновку, що в задачі мова йде про прямокутний трикутник з гострими кутами 30° і 60° (властивість якого було вивчено на попередньому уроці). Проблемою цієї задачі є питання: яка зі сторін прямокутного трикутника (з гострими кутами 30° і 60°) є найбільшою, а яка найменшою?
Розв’язання проблеми (тобто встановлення співвідношення між сторонами й кутами будь_яких трикутників) і є, по суті, основною дидактичною метою уроку.
IV. Актуалізація опорних знань
Виконання усних вправ
1. На промені AX відкладено точки B і D так, що AB > AD. Яка з точок A, B, D лежить між двома іншими?
2. З точки C проведено промені CA, CD, CB так, що промінь CD проходить між променями CA і CB. Порівняйте кути ACD і ACB.
3. Кут 1 є зовнішнім при вершині D трикутника ADC. Порівняйте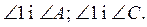 
Чи можна порівняти 
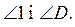Чому?
4. Що можна сказати про кути 1 і 4, якщо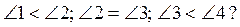 
5. У трикутнику ABC: AB = 4 см, BC = 3 см, AC = 4 см. Що можна сказати про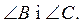 
Чому?
V. Засвоєння нових знань
1°. Формулювання і доведення теореми про співвідношення між сторонами й кутами трикутника.
2°. Формулювання наслідків 1, 2 з теореми про співвідношення між сторонами й кутами трикутника (доведення усно).
3°. Приклади застосування теореми та її наслідків.
Методичний коментар
Тема “Співвідношення між сторонами й кутами трикутника” традиційно вивчалася в 8-9 класах (§ 12 п. 111, 9 клас; § 7 п. 66, 8 клас за підручником О. В. Погорєлова “Геометрія 7-9”). За програмою дванадцятирічної школи ця тема вивчається вже в 7 класі, тому доведення теореми базується на навчальному матеріалі 7 класу, а саме: на аксіомах відкладання та вимірювання відрізків та кутів, властивості кутів рівнобедреного трикутника і зовнішнього кута трикутника. У доведенні застосовується властивість транзитивності числових нерівностей, яку ще не вивчали, але неважко домогтися розуміння учнями цієї властивості на інтуїтивному рівні під час виконання усної вправи № 4.
Доведена теорема про співвідношення між сторонами та кутами в трикутнику дає можливість уже в 7 класі сформулювати важливий наслідок: гіпотенуза більша за катет (тобто в трикутнику гіпотенуза є найбільшою стороною).
Як приклад застосування доведеної теореми та наслідків з неї можна розглянути задачу, запропоновану учням на етапі мотивації навчальної діяльності.
З метою свідомого засвоєння змісту доведених тверджень використовуємо таблицю (до якої звертаємось упродовж уроку).
Таблиця
VІ. Первинне усвідомлення нового матеріалу
Виконання усних вправ
1. Назвіть:
А) найбільшу сторону трикутника DEF, якщо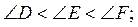 
Б) найменший кут трикутника MNK, якщо MK>NK>MN.
2. З однієї вершини трикутника проведено медіану, бісектрису й висоту,
Причому жодні два з цих відрізків не збігаються. Який із даних відрізків є найменшим?
3. У трикутнику ABC сторона AC найменша. Чи може кут B бути прямим або тупим? Відповідь обгрунтуйте.
4. Учень сказав: “У цьому трикутнику найбільша сторона лежить проти кута 50°”. Доведіть, що він помилився.
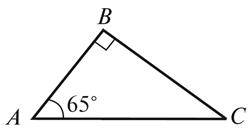
5. Доведіть, що твердження: “У цьому трикутнику найменша сторона лежить проти кута 65°” є неправильним.
Виконання письмових вправ
Рівень А
1. Накресліть трикутник ABC, у якому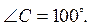 
А) Назвіть найбільшу сторону трикутника й перевірте свою відповідь за допомогою вимірювань.
Б) Виміряйте всі сторони трикутника й перевірте, чи виконується нерівність трикутника для сторін трикутника ABC.
В) Користуючись результатами вимірювань, назвіть найменший кут трикутника.
2. У трикутнику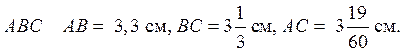 
Назвіть найбільший кут трикутника.
3. У трикутнику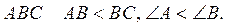 
Назвіть найменший кут трикутника.
Рівень Б
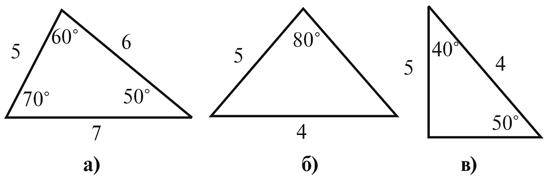
У рівнобедреному трикутнику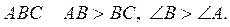 
Назвіть основу трикутника.
Рівень В
У прямокутному трикутнику ABC відрізок CD – бісектриса, проведена з вершини прямого кута. Назвіть найменшу сторону трикутника, якщо кут CDA тупий.
VІІ. Підсумки уроку
Знайдіть помилку на рисунку 7.
VІІІ. Домашнє завдання
Вивчити теоретичний матеріал.
Повторити означення та властивості рівнобедреного трикутника.
Розв’язати задачі.
1. У прямокутному трикутнику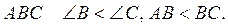 
Назвіть гіпотенузу трикутника.
2. У трикутнику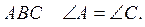 
Назвіть найменший кут трикутника, якщо AC < AB.
3. У прямокутному трикутнику ABC до гіпотенузи проведено висоту CD. Назвіть найменший кут трикутника, якщо AD < BD.
Джерела:
1. Уроки геометрії. 7 клас./ С. П. Бабенко – Х.: Вид. група “Основа”, 2007.- 208 с.
(1 votes, average: 5.00 out of 5)
Loading...