Похідна та її застосування
127.
1) 
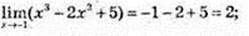
2) 
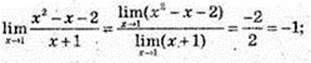
3) 
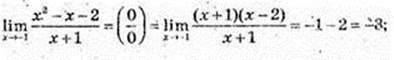
4) 
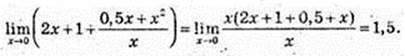
128.
1)
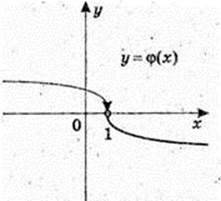
Y = φ(x),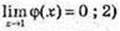 
2)
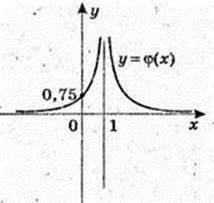
У = φ(x),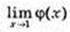 
не існує;
3)
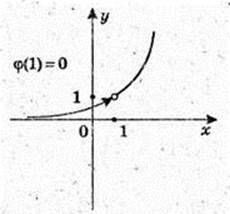
φ(1) = 0.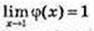 
129.
1) f(x) = x2 + 1, x0 = -1, Δx = 0,1; Δy – ?
Δy = у(х0 + Δх) – у(х0) = f( -0,9) – f(-1) = (-0,9)2 + 1 – ((-1)2 + 1) = 0,81 + 1 – 1 -1 = -0,19;
2)f(x) = x3, x0 = 2, Δx = -1; Δy – ?
Δy = y(x0 + Δx) – y(x0) = у(1) – у(2)
3) 
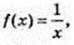x0 = 10, Δx = -5; Δy – ?
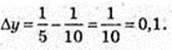
130.
F(x) = x2.
1) f'(x) = 2x; y(5) = 2 × 5 = 10; f’ (-3) = -6;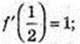 
2) x – ? f'(х) = f(x); 2х = х2; х2 – 2х = 0; х(х – 2) = 0; x1 = 0, x2 = 2.
131.
Y = sin х; у’ = cos х;
1) cos 0 = 1;
2) 
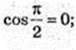
3) cos π = -1.
132.
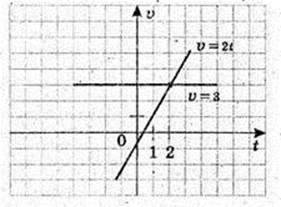
X1 = 3t, x2 = t2, t ≥ο.
1) t -? x1′ = 3; x2′ = 2t; 3 = 2t;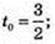 
2) 3 < 2t;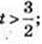 
t? (1,5; +∞);
3) v1 = 3; v2 = 2t.
133.
X = t2 + 1; x’ = 2t; x'(1) = 2; x'(2) = 4;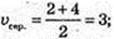 
T0 -? v = 3; 2t = 3; t0 = 1,5.
134.
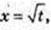t ≥ 0; t0 = 4c;
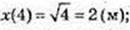
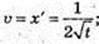
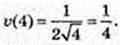
Після 4 c точка рухається за законом x = kt + m,
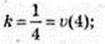
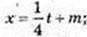х(4) = 2, m – ?
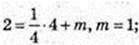
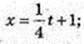
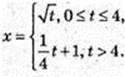
135.
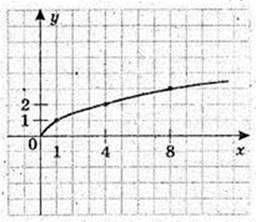
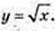
1) A(1; 1).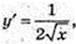 
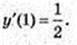
2) B(4; 2).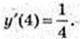 
3) 
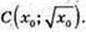
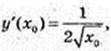x0 > 0.
136.
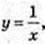
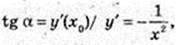
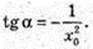
1) x0 = -1. tgα = -1, α = 135°;
2) 
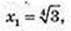
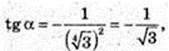
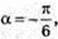α = -30° або α = 150°.
137.
У = x2, у’ = 2х. Рівняння дотичної до графіка функції у = y'(х0) × (х – х0) + y0.
Y'(х0) = 2х0,
1) x0 = 2, y0 = 4; у = 4(х – 2) = 4; у = 4х – 4;
2) x2 = х; x2 – x = 0; х(х – 1) = 0;
X1 = 0; x2 = 1; y'(x1) = 0; y'(x1) = 0; у1 = 0; у'(x2) = 2.
У = 0 × (х – 0) + 0, y = 0 – рівняння першої дотичної;
Y = 2 × (х – 1) + 1, у = 2х – 1 – рівняння другої дотичної.
3)y'(x0) = Ig 135° = – 1; x0 – ?
2х = -1;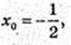 
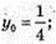
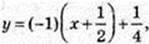
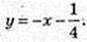
4) у = 1 – х, k = -1; y'(х0) = -1;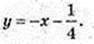 
138.
1) v1 > k; k > 0, v2(2) = 0,v1(2) > v2(2); v1(3) < v2(3);
2) v1сер. = v2сер.
3) друга точка змінила напрям руху в момент t= 2 с.
4) v 1(t) > 0, t > 2; .v2(t) > 0, t > 2; t? (2; +∞).
139.
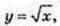x0 = 4, y0 = 2·
1) 
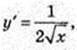
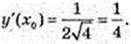
Рівняння дотичної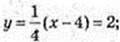 
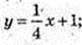
4y = x + 4.
Дана пряма 4у – x = 4. Дотична і пряма збігаються.
2) Пряма у= 4х + 1, k = 4. Дотична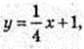 
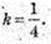
Пряма: і дотична перетинаються.
142.
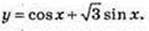
1) 
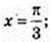
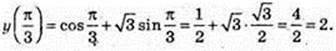
2 )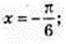 
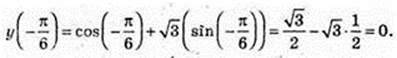
143.
Y = 2х4 – 5×3 + 2х – 5.
1) y = 8х3- 15х2 + 2;
2 )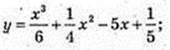 
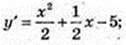
3) y = х(х3 + 4х2 + х – 2) = x4 + 4х3 + x2 – 2х; у’ = 4х3 + 12х2 + 2х – 2;
4) 
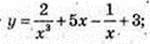
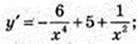
5) 
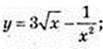
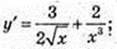
6) у = (х2 + 1) × (5х – 3) = 5х3 – 3х2 + 5х – 3; y’ = 15×2 – 6х + 5;
7) 
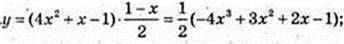
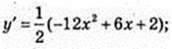у’ = -6Х2 + 3х + 1;
8 )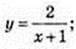 
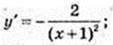
9) 
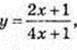х0 = 0;
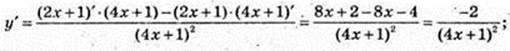
Y'(0) = -2;
10) 
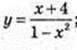
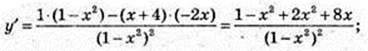
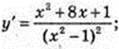
11) 
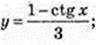
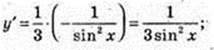
12 )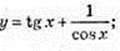 
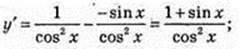
13) у = x × (cos x + 1); у’ = 1 × (cos х + 1) + х × (-sin х) = cosx – х sin х + 1;
14) 
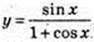
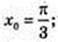
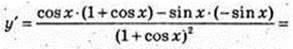
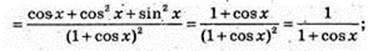
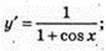
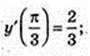
15) 
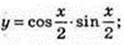
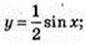
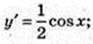
16) у = In 3 × 3x; y’ = In 3 × 32 × In 3 = (In 3)2 × 32;
17) 
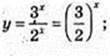
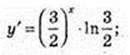
18) 
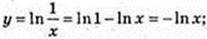
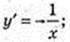
19) 
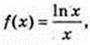x0 = 1;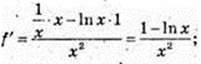 
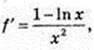In 1 = 0, f'(x0) = 1;
20) у = Ig x + 2х;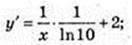 
21) у = ln(-х);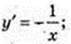 
22) у = log2(3- 2х), x0 = 1;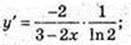 
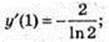
23) y = 102x-1; у’ = 2 × 102x-1 × In 10.
144.
Y = 2х3 – 2х2 + x – 1.
1) x0 – ? у'(х0) = 1; y’ = 6х2 – 4х + 1; 6х2 – 4х + 1 = 0 + 1; 6х2 – 4х = 0; x1 = 0,
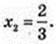А(0; -1).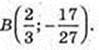 
2)x – ? у'(х0) = 3; 6х2 – 4х + 1 = 3; 6х2 – 4х – 2 = 0; Зх2 – 2х – 1 = 0; x = 1,
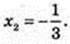А(1; 0),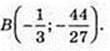 
145.
1) х = 1- 0,1t, t0 = 3. x'(t) = -(0,1)t × In 0,1;
Х'(3) = -(0,1)3 × (-In 10) = In10 × 0,001 = 0,0023;
2) 
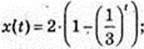
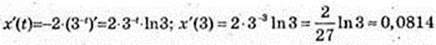
146.
У = x2 × In х.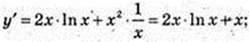 
У'(1) = 1; tg α = у'(1) =1; tg α = 1;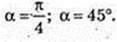 
147.
Y = 3 cos x + 2 sin х; у’ = -3 sin х + 2 cos х, x0 = 0, у0 = 3;
1) у'(0) = 2. Рівняння дотичної: у = y'(0) × (х – x0) + y0;
Y = 2 × х + 3; у = 2х + 3;
2) у’ = -3 sin x + 2 cos х;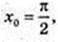 
y0 = 2,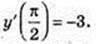 
Рівняння дотичної: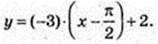 
3). 
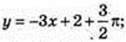
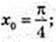
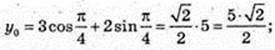
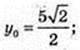
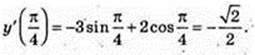
Рівняння дотичної: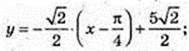 
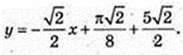
148.
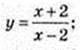
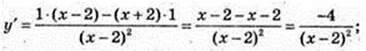
α = 135°, tg 135° = -1; tg 135° = y'(x0); -1 = y'(x0); x0 – ?
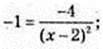(x – 2)2 = 4; x – 2 = 2; x1 = 4, x2 = 0;
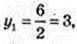A(4;3); y2 = -1,B(0; -1).
149.
У = x2 – 3х + 2; y’ = 2x – 3.
1) y'(0) = -3; x = 0, у = 2. Рівняння дотичної: у = -3 × x + 2.
2) x – ? x2 – 3х + 2 = 0; х 1 = 1, x2 = 2, у1 = 0, у2 = 0.
У'(x 1) = -1, рівняння дотичної; у = -(х – 1) = – х + 1.
У'(x2) = 1, рівняння дотичної у = x – 2.
3) у = x2 – 3х + 2; у’ = 2х – 3.
X – ? x2 – 3х + 2 = x2 – 1; -3х + 2 = -1; -3х = -3; x0 = 1,
У0 = 0; у'(1) = -1; у = -(х -1). Рівняння дотичної: у = – х + 1.
150.
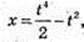t ≥> о.
1) 
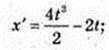x'(t) = 2t3 – 2t (м/с) = v(t);
2) t – ? х'(t) = 0; t3 – t = 0; t(t – 1)(t +1)=0; t1 = 0 с, t2 = 1 с, t3 ≠ -1, t > о.
3) х = о, t -?,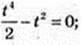 
t2(t2 – 2) = 0; t1 = 0,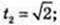 
V(0) = 0 м/с;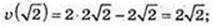 
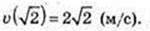
4) v”(t) = 6t2 – 2; t0 =1; v”(t0) = 6 – 2 = 4; v”(1) = 4 м/с2.
151.
X = 2 sin πt, t ≥ 0.
1) v = 2π cos πt;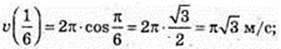 
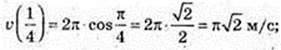v(1) = 2πcosπ = -2π м/с.
2) t – ? v(t) = 0; 2π cos πt = 0; cos πt = 0;
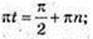
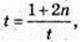n = 0,1,2,3,4,…
3) v(t) = 2π cos πt ≤ 2π, якщо cos πt =1; πt = 2πk, t = 2k, k = 0, 1, 2, 3, …
4) v'(t) = -2π2 sin πt = (-π2) × 2 sin πt; v'(t) = (-π2) × x(t), k =-π2.
152.
X = 2t3 – 3t2 – 12t + 1, t ≥ 0.
1) v = x'(t) = 6t2 – 6t – 12 = 6(t2 – t – 2);
V'(t) = (6 × (t2 – t – 12))’ = 6 × (2t – 1);
V'(3) = 6 × (0 – 1) = 30 м/c2;
2) t-? v'(t) = 0; 6 × (2t – 1) = 0; 
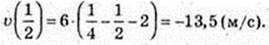
153.
1) 
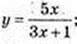
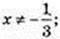
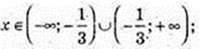
2) 
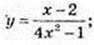
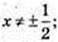
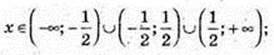
3) 
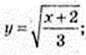
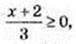x ≥ -2; x? [-2; +∞);
4) 
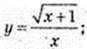
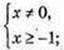x? [-1; 0) 
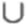(0; +∞).
154.
1) 
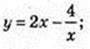
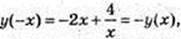функція непарна;
2) 
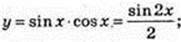
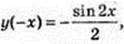функція непарна;
3)у = е-2х + е2х; у(-х) = е2х + e-2x = у(х), функція парна;
4) у = x2 + 1; y(-x) = (-х)3 + 1= – х3+ 1 ≠ ± у(х), функція ні парна, ні непарна.
155.
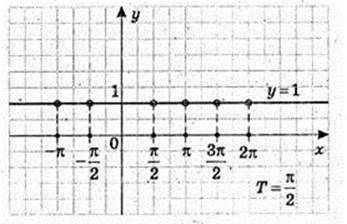
1) у = sin 2х;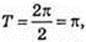 
T = π;
2) 
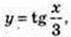
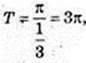T= 3π;
3) 
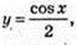Τ=2π:
4) y = tg x ×ctg x; у = 1,якщо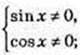 
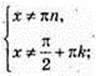
156.
Y = log0,5x, y = ex, y= 1 – x,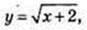 
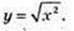
Серед цих функцій зростаючі – це у = еx та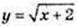 
У своїй області визначення.
157.
1) f(x) = x3 + 2x + 1, D(f ) : x? R.
Функція зростає, якщо її похідна є невід’ємною.
Знайдемо f'(x). f'(x) = 3х2 + 2 > 0, x? R, тобто f(x) – зростаюча.
2) f(x) = 1 + 2x + sin х, D(f): х? R.
F'(x) = 2 + cos x > 0, тому що |cos х| ≤ 1. f(x) зростає всюди.
158.
1) у = 2х3 – 3х2 – 72х + 6, D(f): х? R. у’ = 6х2 -6х – 72.
Знайдемо нулі похідної: 6(x2 – х – 12) = 0; x1 = 4, x2 = -3.
Розіб’ємо область визначення функції на інтервали і
Визначимо знаки похідної на кожному з інтервалів.
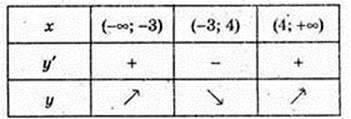
Функція зростає на проміжках (-∞; -3] і [4; +∞) (f'(x) ≥ 0).
Функція спадає на проміжку [-3; 4] (f'(x) ≤ 0).
2) у = 9х4 – 16×3 + 6х2 + 3, D(y): х? (-∞; +∞),
У’ = 36×3 – 48×2 + 12x = 0; 12x(3×2 – 4x + 1) = 0; x1 = 0;
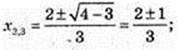x2 = 1;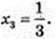 
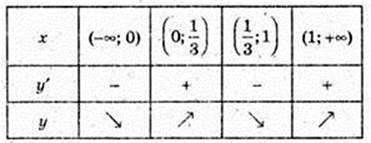
Функція зростає на проміжках
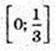І [1;+∞) (y’ ≥ 0).
Функція спадає на проміжках (-∞; 0] і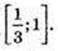 
3) 
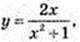D(y): x? R. 
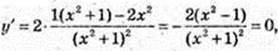x = ±1.
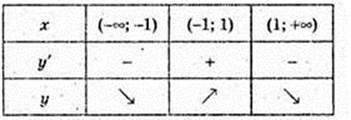
Функція спадає на проміжках (-∞; -1] і [1;.+ ∞) (у’ ≤ 0).
Функція спадає на проміжку [-1; 1] (y’ ≥ 0).
4) у = x3 + 2х2 – 4х +1, D(y): x? R.
У’ = 3х2 + 4х – 4 = 0;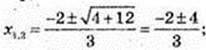 
X1 = -2;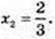 
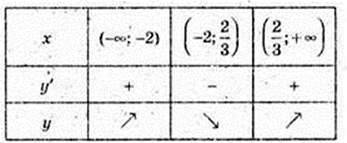
Функція зростає на проміжках (-∞; -2] і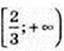 
(у’ ≤ 0).
Функція спадає на проміжку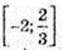 
(y’ ≤ 0).
5) y = 3×4 – 5×3 + 2, x? R. у’ = 12х3 – 15×2 = 3х2(4х – 5) = 0;
X1 = 0;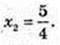 
Функція спадає на проміжку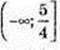 
(y’ ≤ 0).
Функція зростає на проміжку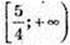
(y’ ≥ 0).
6) у = (х + 3)(x – 1), D(y): x? R. у = (х + 3)(x2 – 2х + 1) = x3 + х2 – 5х + 3;
У’ = 3х2 + 2х – 5 = 0;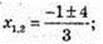 
x1 = 1;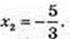 
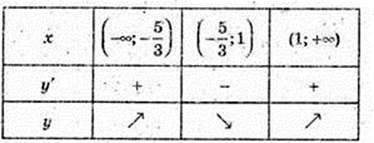
Функція зростає на проміжках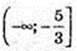 
і [1;+ ∞) (у’ ≥ 0).
Функція спадає на проміжку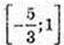 
(у’ ≤ 0).
7) у = 1-(х – 5)х3 = 1 + 5х3 – x4, D(y): х? R.
Y’ = 15×3 – 4х3 = x2(15 – 4х) = 0; x1 = 0;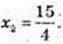 
Функція зростає на проміжку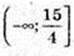 
(y’ ≥ 0).
Функція спадає на проміжку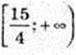 
(у’ ≤ 0).
8) у = ех – x + 1, D(y) ? R. у’ = ex – 1 = 0; х = 0.
Функція спадає на проміжку (-∞; 0] (у’ ≤ 0).
Функція зростає на проміжку [0; +∞”) (y’ ≥ 0).
9) у = xex, D(y): x? R. у’ = еx + хех = еx(х + 1) = 0; x = -1.
Функція спадає на проміжку (-∞; -1] (у’ ≤ 0).
Функція зростає на проміжку [-1; +∞) (у’ ≥ 0).
10) у = x(ln x – 2), D(y): x? (0; +∞).
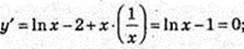x = e.
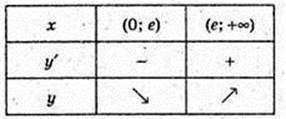
Функція спадає на проміжку (0; е) (у’ ≤ 0).
Функція зростає на проміжку (е; +±) (y’ ≥ 0).
11). 
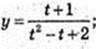D(y): t? R. t2 + 2t – 3 = 0;
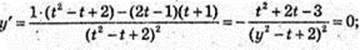
T2 + 2t -3 = 0; t1 = -3, t2 = 1.
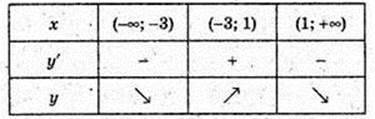
Функція спадає на проміжках (-∞; -3] і [1; +∞).
Функція зростає на проміжку [-3; 1] (y’ ≥ 0).
159.
1) 3 малюнка 123 видно, що f(x) = 0 при x = 0 I x = 1. (Дотична до графіка функції
В цих точках горизонтальна.) Тобто 2 корені: x1 = 0, x2 = 1.
2) f(x) < 0 (функція спадає). З малюнка видно, що ця умова виконується на проміжках (-2; 0)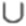 
(1; 3).
160.
Функція зростає на проміжку [-2; 1] (y’ ≥ 0) і спадає на проміжку [1; 2] (у’ ≤ 0).
161.
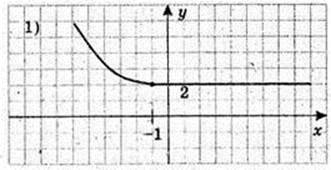
1) Наприклад, f'(x) < 0, f(x) – спадає; f'(x) = 0, f(x) – стала.
2) Дивись рисунок
162.
4х5 + x3 + 5 = 0.
Розглянемо функцію у = 4×5 + x3 + 5, D(y): х? R. Її похідна у’ = 20х4 + 3×2 ≥ 0 (x? R), тобто функція монотонна (зростаюча), отже, рівняння 4х5 + х3 + 5 = 0 має не більше, ніж один корінь. Неважко перевірити, що х = -1 є коренем даного рівняння.
163.
1) f'(x) > 0, х? (-4; -3) і (-1; 4);
2) f'(x) < 0, x? (-3; -1) і (4; 6);
3) f'(x) = 0, x = -3, х =-1, x = 4.
4) Точку екстремуму: x1 = -3, уmax = -1; x2 = -1, ymin = -3; x3 = 4, ymax = 1.
5) Таких точок немає.
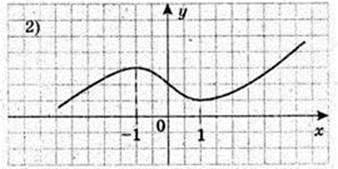
1) f'(x) > 0, х? (0; 2);
2) f'(x) < 0, х? (-3; 0) і (2, 4)
3) f'(x) = 0,x = 0.
4) Точки екстремуму: x1 = 0, уmin = -2; x2 = 2, у = 0.
5) y'(x) нe існує, x = 2.
164.
1) у = x3 – 2х2 + 7x + 3, D(у): х? R.
Y’ = 3х2 – 4х – 7=0;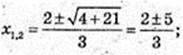 
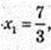x2 = -1.
2) у = x3 + x2 – 5x + 4, D(y): x? R.
У’ = 3х + 2х – 5 = 0;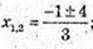 
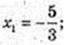x2 =1.
3) y = x4 – x3 + 7. D(y): x? R.
У’ = 4х3 – 3х2 = 0; х2(4х – 3) = 0;
X1,2 = 0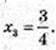
4) у-(1 + х)ех, x? R. у’ = ех + (1 + х)еx = ех(х + 2) = 0; x = -2.
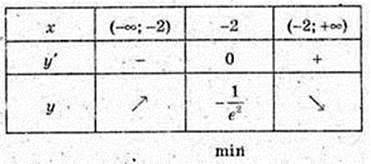
5) у = In x – 3x, D(y): х? (0; +∞).
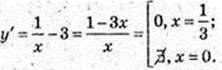
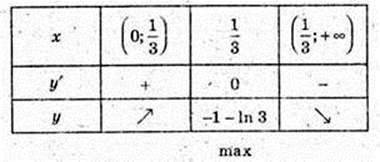
6) 
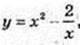x є (-∞; 0) (0; +∞).
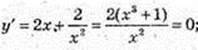x = -1.
7) 
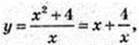x? (-∞; 0) 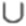(0; +∞).
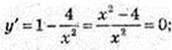x = ±2.
8) у = 2х In x, D(y): x? (0; +∞). у’ = 2(ln х + 1) = 0; In х = -1;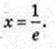 
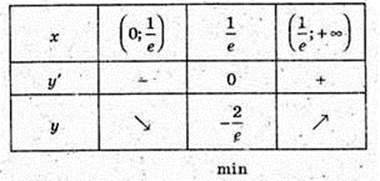
9) 
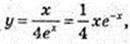x? R.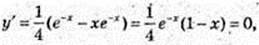 
x = 1.
165.
1) 
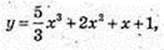D(y): х? R.
У’ = 5х2 + 4x + 1 = 0;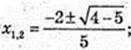 
D< 0, дійсних коренів немає і 5х2 + 4x + 1 > 0, x? R.
Функція всюди зростає, екстремумів немає,
2) у = 2 x + sin х, x? R. у’ = 2 + cos х > 0 всюди, тому |cos x| < 1.
Екстремумів нема. Функція всюди зростає.
166.
1) Критичні точки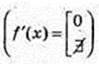 
x1 = -1, x2 = 1, x3 = 3.
2) g(3), тему що x = 3 – точка максимуму.
На проміжку [2; 3] у’ > 0, тому функція зростає і g(3) > g(2).
167.
1) у = х3- 3х.
1. D(y): x? R.
2. Непарна, у(-х) = – х3 + 3x = -(х3- 3) →симетрія відносно начала координат.
3. Неперіодична.
4. у = 0, х(х2 – 3) = 0, x1 = 0, 
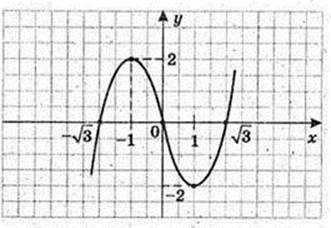
5. y’ = 3х2 – 3 = 3(х2 – 1) = 0О, x = ±1.
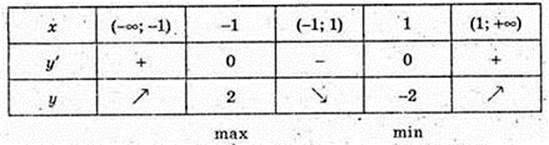
2) у = 3×2 – x3.
1 .D(y): x? R.
2. Загального виду.
3. Неперіодична.
4. у = 0, х2(3 – х) = 0, x1 =0,x2 = 3.
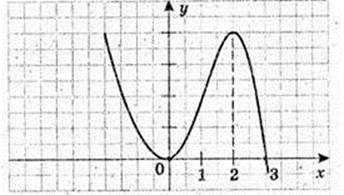
5. у’ = 6x – 3х2 = 0,3х(2 – х) = 0, x = 0, х = 2.
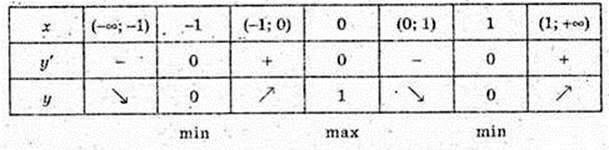
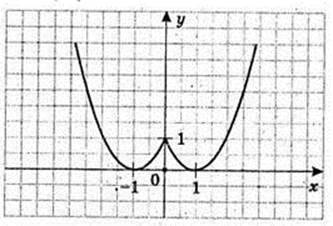
4) y = x4 – 2×2 + 1, у = (x2 – 1)2.
1. D(y): x? R.
2. Парна, f(-x) = f(х), графік симетричний відносно вісі Oy.
3. Неперіодична.
4. у = 0, x = ±1, у ≥ 0.
5. y’ = 2(х2 – 1) × 2x = 4x(x2 – 1) = 0, x1 = 0, x2 3 = ±1.
5) у = 2×4 – 8х.
1. D(y): x? R.
2. Загального виду.
3. Неперіодична.
4. у = 0, 2х(х3 – 4) = 0, x1 = 0,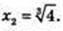 
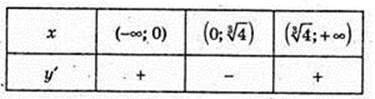
5. у’ = 8х3 – 8 = 8(x3 -1) = 0, x = 1.
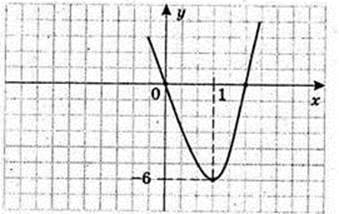
6) у = х3(3х – 4) = 3х4 – 4х3.
1. D(y): x? R.
2. Загального виду.
3. Неперіодична.
4. у = 0, x1 = 0,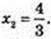 
5. у’ = 12×3 – 12×2 = 12×2(x -1) = 0, x1 = 0, x2 = 1.
168.
X = (t – 33)(t – 1) – 1, t ≥ o.
V(t) = x'(t) = 3(t – 3)2(t – 1) + (t – 3)3 × 1 = (t – 3)2(3t – 3 + t – 3) = 2(t – 3)2(2t -3);
V(t) = 2(t – 3)2(2t – 3), t ≥ 0;
V'(t) = 2; (2(t – 3)(2t – 3) + (t – 3)2 × 2) = 4(t – 3)(2t – 3 + t – 3) = 12(t – 3)(t – 2);
V'(t?) = 0; t = 2, t = 3.
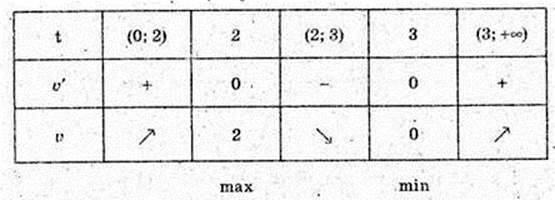
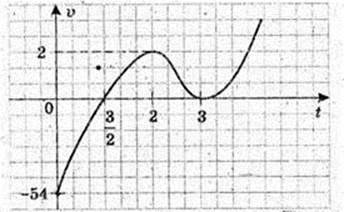
168.
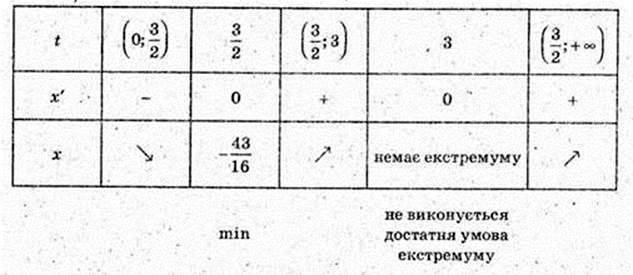
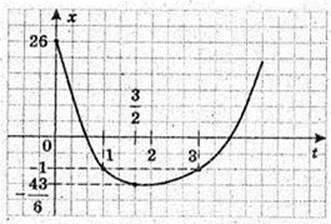
X = (t – 3)3(t – 1)- 1.
T = 0, x = 26.
X’ = 3(t – 3)2(t – 1) + (t – 3)2 × 1 = 2(t – 3)(2t – 3) = 0; t1 = 3,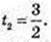 
169.
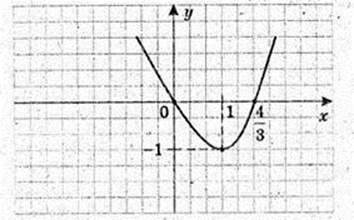
X3 – 6X2 + 9X = 4.
Розглянемо функцію у(х) = x3- 6×2 + 9x.
Побудуємо її графік. у = 0: х(х2 – 6х + 9) = 0, x1 = 0, x2 = 3.
У(х) = х(х – 3)2.
У’ = 3×2 – 12х + 9 = 3(х2 – 4х + 3) = 0, x1 = 1, х2 = 3.
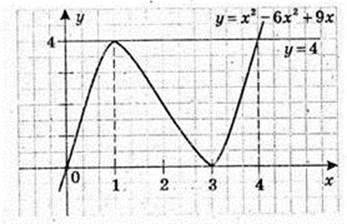
Графік правої частини рівняння є пряма у = 4.
Вона перетинає графік лівої частини рівняння
У = x3 – 6×2 + 9x в двох точках x = 1і x = 4.
Отже, рівняння має 2 корені: х = 1, x = 4.
170.
1) y найб. = 1 при x = 1, y найм. = 0 при x = 0;
2) y найб = 2 при 2 ≤ х ≤ 3, y найм. =1 при х = 4;
3) y найб = 5 при x = 8, y найм. = 3 при х = 5 і х = 7;
4) y найб. = 4 при x = 6, y найм. =0 при X = 0.
171.
1) у = 3х – 2, y’ = 3 ≠ 0, y найм. = y(-1) = -5, y найб = y(3) = 7;
2) y = 2 – 3х, у’ = -3 ≠ 0, y найм. = y(3) = -7, y найб = y(-1) = 5;
3) y = x2 – 6x + 8, y’ = 2х – 6 = 0, х = 3 ? [1,4].
Y найб = 3 при x = 1, y найм.= -1 при x = 3.
4) у = х2 – 6х+ 8, y’ = 2х – 6 = 0,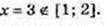 
Y найб = 3 при x = 1. y найм. = 0 при x = 2.
5) 
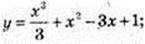y’ = х2 + 2х – 3 = 0, x1 =-3, x2= 1.
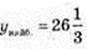при x = 4; 
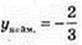при x = 1.
6 )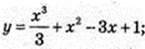 
Y’ = x2+ 2x – 3 = 0, x1 = -3 ? [-4; 0],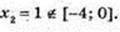
Y найб = 10 при x = -3, y найм. = 1 при х = 0.
7) y = cos x + sin х; y’ = – sin х + cos х = 0| : cos х; tg х= 1;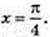 
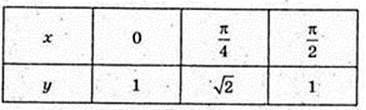
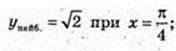y найм. = 1 при x = 0,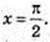 
8) y = tg x +2x;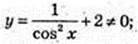 
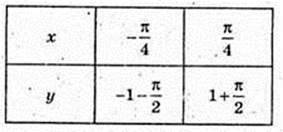
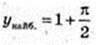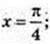
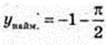при 
при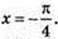 
9) y = xex. y’ = ex(1 + x) = 0,x = -1 ? [-2; 0].
Y найб = 0; при x = 0;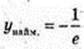 
при х = -1.
172.
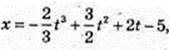t ≥ о
1) x(0) =-5;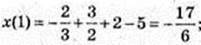 
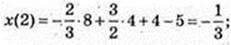
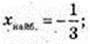X найм. = -5.
2) v = x'(t) = -2t2 + 3t + 2. t – ?
V(t) = 0. -2t2 + 3t+ 2 = 0; 2t2 – 3t – 2 = 0; t1 = 2,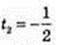 
– не задовольняє умові.
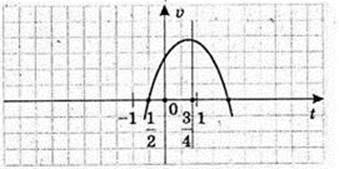
V’ = -4t + 3. t – ? v’=0,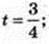 
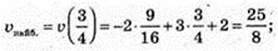
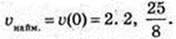
173.
1) 
S = x × (160 – x) =- x2 + 160х. S найб. – ?
S’ = -2x + 160; 160 – 2x = 0; x = 180. Розмір ділянки: 80 x 80.
(1 votes, average: 5.00 out of 5)
Loading...