Головна ⇒ 📌Математика ⇒ ПРО РІВНІСТЬ ГЕОМЕТРИЧНИХ ФІГУР

ПРО РІВНІСТЬ ГЕОМЕТРИЧНИХ ФІГУР

РОЗДІЛ 3 ТРИКУТНИКИ

& 11. ПРО РІВНІСТЬ ГЕОМЕТРИЧНИХ ФІГУР

На малюнку 139 зображено два трикутники. Уявіть, що один із них накреслений на папері, а інший – на прозорій плівці. Переміщаючи плівку, другий трикутник можна сумістити з першим. Кажуть: якщо дані трикутники можна сумістити накладанням, то вони – рівні. Рівними один одному бувають не тільки трикутники, а й відрізки, кути, кола та інші фігури.

Зображені на малюнку 140 фігури також рівні, бо їх можна сумістити, перегнувши аркуш паперу по прямій l. А фігури, зображені на малюнку

141, – нерівні, їх не можна сумістити.

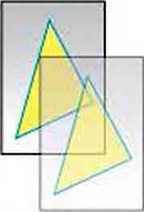
Мал. 139

Мал. 140

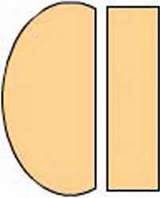
Мал. 141

Для позначення рівних фігур використовують знак рівності ” = “. Наприклад АВ = КР, ∠A = ∠B, ∆АВС = ∆КРТ.

Якщо кожна з двох фігур дорівнює третій, то перша і друга фігури також рівні.

З рівними фігурами часто доводиться мати справу багатьом фахівцям. У формі рівних прямокутників випускають листи жерсті, фанери, скла, облицювальні плитки, паркетини тощо. Рівні всі аркуші паперу з однієї пачки, відповідні деталі двох машин однієї марки.

Щоб

з’ясувати, чи рівні дві фігури, можна спробувати їх сумістити. Але на практиці це не завжди можна зробити. Наприклад, таким способом не можна з’ясувати, чи рівні дві земельні ділянки. Тому доводиться шукати інші способи, виявляти ознаки рівності тих чи інших фігур. Наприклад, якщо радіуси двох кіл рівні, то рівні й самі кола. Це – ознака рівності кіл. У наступному параграфі ми розглянемо ознаки рівності трикутників.

Зверніть увагу! Трикутник з вершинами А, В і С можна позначати по-різному: ∆АВО, ∆ВСА, ∆САВ, ∆BАС і т. д. Однак для зручності домовимося, що коли пишуть ∆АВС = ∆КРТ, то розуміють, що ∠A = ∠K, ∠B = ∠P, ∠C =∠T, AB = КР, АС = КТ, ВС = РТ.

Для допитливих

Слово “рівність” у математиці й інших науках вживається досить часто. Говорять, зокрема, про рівність чисел, рівність виразів, рівність значень величин. Рівність геометричних фігур – це відношення. Воно має такі властивості:

1) кожна фігура дорівнює сама собі;

2) якщо фігура А дорівнює фігурі В, то й фігура В дорівнює фігурі А;

3) якщо фігура А дорівнює фігурі В, а фігура В дорівнює фігурі С, то фігури А і С – також рівні.

Нерідко з рівності одних фігур чи величин випливає рівність інших, але не завжди. Наприклад, якщо трикутники рівні, то і їхні периметри рівні. Але якщо периметри двох трикутників рівні, то це ще не означає, що рівні й самі трикутники. Так само: якщо трикутники рівні, то і їхні площі рівні. Але якщо площі двох трикутників рівні, це ще не означає, що й трикутники рівні.

Досить часто для обгрунтування рівності тих чи інших фігур треба обгрунтувати рівність деяких трикутників. Ось чому питання про рівність трикутників у геометрії дуже важливе: більшість теорем шкільної геометрії доводять, користуючись ознаками рівності трикутників.

Запитання і завдання для самоконтролю

1. Які фігуфи називають рівними?

2. Яким знаком позначають рівність фігур?

3. Наведіть приклади предметів довкілля, що МАЮТЬ форму рівних геометричних фігур.

4. Сформулюйте властивості відношення рівності фігур.

5. Сформулюйте ознаку рівності двох кіл.

Виконаємо разом

1. Чи рівні кути, зображені на малюнку 142?

– Сторони кута – промені. Хоч на малюнку вони зображені нерівними відрізками, але слід уявляти їх нескінченними променями. Оскільки кожний із цих кутів дорівнює 35° (перевірте), то вони – рівні.

2. Доведіть, що трикутники не можуть бути рівними, якщо не рівні їх найбільші куги.

– Нехай у трикутниках ABC і KPT ∠А > ∠В > ∠C, ∠К > ∠Р > ∠T. Якби дані трикутники були рівні, їх можна було б сумістити.

Тоді найбільший кут А трикутника ABC сумістився б із найбільшим кутом К трикутника КРТ. Це неможливо, оскільки АА ≠ АК. Отже, дані трикутники не можуть бути рівними.

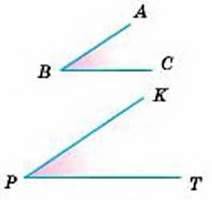
Мал. 142

ЗАДАЧІ І ВПРАВИ

Виконайте усно

317. Чи рівні дві фігури на малюнку 143?

318. Чи правильно, що коли даний трикутник прямокутний чи тупокутний, то й рівний йому трикутник також відповідно прямокутний чи тупокутний?

319. Чи рінні трикутники, зображені на малюнку 144?

320. Середини сторін квадрата ABCD послідовно сполучили відрізками так, що утворилося 4 трикутники (мал 145). Чи правильно, що кожний із цих трикутників дорівнює іншому?

Мал. 143

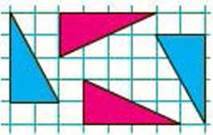
Мал. 144

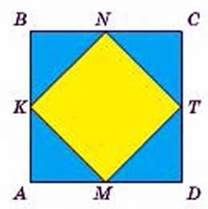
Мал. 145

321. Чи рівні як геометричні фігури символи:

А) О і 0;

Б) < і >;

В) = і |;

Г) Г і L?

322. Чи можуть бути рівними прямокутний і тупокутний трикутники? А прямокутний і гострокутний?

323. Трикутники ABC і КРТ – рівні. Чи рівні їх периметри?

324. Периметри трикутників ABC і КРТ – рівні. Чи рівні трикутники?

325. Один із двох суміжних кутів можна сумістити з іншим. Які це кути?

326. Які з фігур, зображених на малюнку 146, – рівні?

Мал. 146

327. Чи можуть бути рівними трикутники, найменші сторони як, не рівні?

328. Пряма, яка проходить через центр кола, розбиває його на два півкола. Чи рівні вони? Як можна одне півколо сумістити з іншим?

329. Знайдіть периметр трикутника КРТ, якщо ∆КРТ = ∆ABC, АВ = 3 см, ВС = 4 см і АС = 5 см.

330. Трикутники ABC i A1В1C1 наклали один на одний так, що сумістилися вершини А і А1, В і B1, С і C1. Чи сумістяться сторони АВ і A1B1, АС і A1C1, ВС і B1C1? А медіани АМ i A1M1?

331. Фігури ABCD і HTPK рівні (мал. 147). Знайдіть кут Т і відстань КТ, якщо BD = 3,8 см і ∠B = 70°.

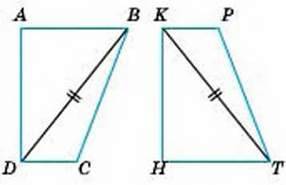
Мал. 147

332. Знайдіть кути трикутника ABC, якщо ∆АВО = ∆КРТ, АК = 60° i ∠P = 60°.

333. Сторони АВ і РТ – не рівні. Чи можуть бути рівними трикутники ABC і КРТ?

334. Кути ABC і КРТ – рівні. Скількома способами один із них можна сумістити я іншим?

335 ∆АВС – тупокутний, а кути трикутника А1В1С1 пропорційні числам 5, 6 і 7. ЧИ можуть бути рівними ці трикутники?

336. ∆АВС = ∆MNK, ∠N = 2∠A. Знайдіть кути трикутників, якщо АС = 60°.

337. ∠АОВ і ∠ВОС – суміжні, ∠ВОС – ∠АОВ = 30°. ∠МКР і ∠PKN – суміжні, ∠МКР : ∠PKN =7 : 5. Укажіть пари рівних кутів, якщо вони є.

338. Периметри прямокутників ABCD і MNP К дорівнюють но 28 см. Побудуйте ці прямокутники так, щоб:

А) вони були рівними; б) вони не були рівними.

339. Одна зі сторін прямокутника ABCD на 3 см більша за іншу, а його периметр дорівнює 34 см. Площа прямокутника MNPК дорівнює 70 см2. Чи можуть бути рівними ці прямокутники? А якщо площа прямокутника МNРК дорівнює 72 см2?

340. На координатній площині дано точки А (1; 4), В (2; 7), С (2; 4), D (2; 1), К (4; 1). Чи рівні трикутники ABC і ABC? А трикутники АВС i СDK?

341. Прямокутники ABCD і КРТМ дорівнюють один одному і АВ = КР -10 см. Знайдіть КМ, якщо АС = 26 см і периметр трикутника KРТ дорівнює 60 см.

342. Точки А, В, С, В, Е ділять коло з центром О на 5 рівних дуг. Чи рівні відрізки АВ і ЕА? А трикутники ОВС і ОАЕ?

343. Чи правильно, що кожна пряма, проведена через центр О квадрата або прямокутника (мал. 148), розрізає його на дві рівні фігури?

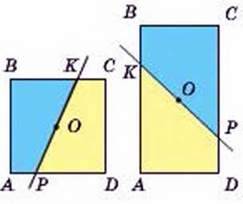
Мал. 148

Практично завдання

344. В основу багатьох українських вишивок і орнаментів покладені рівні ромби різного кольору (мал. 149 і 160). Створіть орнамент з рівних: а) квадратів; б) трикутників; в) відрізків.