Прямокутна система координат на площині
УРОК № 22
Тема. Прямокутна система координат на площині
Мета уроку: узагальнення та систематизація матеріалу про декартову прямокутну систему координат.
Тип уроку: комбінований.
Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13].
Вимоги до рівня підготовки учнів: описують прямокутну систему координат. Застосовують вивчені означення до розв’язування задач.
Хід уроку
I. Перевірка домашнього завдання
Перевірити наявність виконаних домашніх завдань та відповісти на запитання,
II. Аналіз результатів тематичної контрольної роботи № 2
ІІІ. Узагальнення й систематизація знань учнів
Узагальнити та повторити матеріал, пов’язаний з координатною площиною, відомий учням з курсу математики 6 класу та алгебри 7-8 класів можна в процесі виконання завдань та фронтальної бесіди з використанням таблиці [13] та рис. 126.
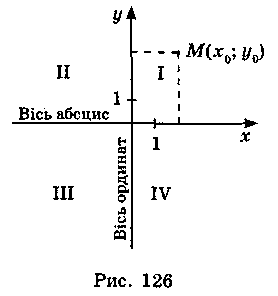
Запитання до класу
1. Що називається прямокутною системою координат? 2. Як у прямокутній системі координат називають горизонтальну пряму Ох; вертикальну пряму Оу; точку О(0; 0)? 3. Що таке абсциса
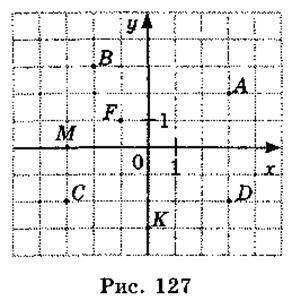
7. Що можна сказати про координати точки, яка лежить на осі абсцис? на осі ординат? 8. Побудуйте точки: А(3; 0), В(3; 4), С(-3; -2), D(-4; 0), E(3; -2), F(-3; 2).
У ході виконання цих вправ учні повинні усвідомити, що задати систему координат на площині означає, що кожній точці площини можна поставити у відповідність впорядковану пару дійсних чисел х і у і, навпаки, кожній парі х і у – єдину точку площини.
IV. Виконання вправ
1. У яких точках на координатній площині дорівнюють нулю абсциси? ординати? 2. Де розташовані на координатній площині точки, абсциси яких дорівнюють 5? ординати яких дорівнюють -5? 3. Побудуйте на координатній площині чотирикутник ABCD, якщо А(-3; 2), В(3; 2), С(-3; -1), D(3; -1). Визначте вид чотирикутника, знайдіть периметр і площу цього чотирикутника. 4. Нехай А(-5; -1), В(-1; -1), С(-1; -3) – координати трьох вершин прямокутника. Знайдіть координати четвертої вершини. Чому дорівнюють периметр і площа цього прямокутника? 5. Дано точку А(2; 3). Знайдіть координати основи перпендикуляра, опущеного з точки А на вісь Ох; на вісь Оу. 6. Де на координатній площині розташовані всі точки, абсциси яких дорівнюють їх ординатам? 7. Побудуйте на координатній площині всі точки з абсцисою х і ординатою у такі, що:
А) |x| = 3, |у| = 2;
Б) |x| = 3, |у| ? 2;
В) |х| ? 3, |y| = 2;
Г) |x| ? 3, |у| ? 2.
8. При якому значенні х точки А(2x – 1; 0) і В(x + 1; 5) лежать на одній прямій, яка паралельна осі Оу? 9. Знайдіть площу трикутника з вершинами в точках А(0; 0), В(1; 2), С(3; 1).
V. Домашнє завдання
1. Повторити відомості про декартові координати на площині. 2. Виконати завдання. 1) Побудуйте квадрат ABCD так, щоб вершина С мала координати (-2; 2), а діагоналі квадрата перетиналися в початку координат. Знайдіть координати точок А, В, D та периметр і площу цього квадрата. 2) Зобразіть на координатній площині всі точки (х;у), якщо:
А) у = 0, х? 2;
Б) -2 ? у? 2, х? 0;
В) |x| ? 2, у? 1;
Г) |х| ? 2, у? -2.
VI. Підбиття підсумків уроку
Завдання класу
1. Поясніть, що таке декартова прямокутна система координат. 2. Дано точку А(-3; 4). Укажіть координати основ перпендикулярів, які опущені з цієї точки на координатні осі. Чому дорівнює відстань від точки А до координатних осей? до початку координат?