Рівноприскорений рух. Прискорення. Швидкість тіла і пройдений шлях під час рівноприскореного прямолінійного руху. Графіки руху
КІНЕМАТИКА
Урок № 6
Тема. Рівноприскорений рух. Прискорення. Швидкість тіла і пройдений шлях під час рівноприскореного прямолінійного руху. Графіки руху
Мета: сформувати знання про рівноприскорений рух і прискорення, швидкість тіла і пройдений шлях під час рівноприскореного прямолінійного руху, графічне зображення модуля переміщення на графіку швидкості в рівноприскореному русі, умінь виводити формулу проекції переміщення; виробляти вміння обчислювати прискорення, знаходити проекцію миттєвої швидкості за проекціями початкової
Тип уроку: урок вивчення нового навчального матеріалу.
Унаочнення: демонстрування рівноприскореного прямолінійного руху, ППЗ “Фізика-9” від “Квазар-Мікро”.
ХІД УРОКУ
I. Аналіз результатів самостійної роботи
Показати кращі роботи учнів, спинитись на поясненні типових помилок.
II. Вивчення нового матеріалу
У ході лекції з використанням демонстрацій учні конспектують матеріал.
Рух матеріальної точки, під час якого її швидкість за будь-які однакові проміжки часу
0, а через певний час t його швидкість дорівнює T, то вектор прискорення прямолінійного рівнозмінного руху можна визначити за формулою: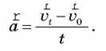
Прискорення – це векторна фізична величина, що дорівнює відношенню зміни швидкості до часу, протягом якого ця зміна відбулася.
Якщо швидкість за будь-які однакові проміжки часу збільшується на ту саму величину, то такий рух називається рівноприскореним. Якщо швидкість тіла зменшується часом на ту саму величину, то рух називають рівносповільненим. Якщо рівнозмінний рух прямолінійний, то за одну з осей координат (наприклад, Ox) зручно взяти пряму, по якій рухається матеріальна точка, а за її додатний напрям – напрям початкової швидкості 0. Тоді прискорення обчислюють як скалярну величину – проекцію вектора прискорення, тому формулу можна записати в скалярній формі:
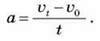
Проекція вектора прискорення матиме знак “+”, якщо напрям вектора прискорення збігається з напрямом вектора 0, і знак “-” у випадку протилежного напряму цих векторів. На підставі формули встановлюють одиниці вимірювання прискорення. Як одиницю прискорення в СІ взято прискорення 1 м/с2 – це прискорення такого рівнозмінного руху, під час якого швидкість за 1 с змінюється на 1 м/с.
Для побудови графіка прискорення прямолінійного рівнозмінного руху по осі ординат відкладають прискорення, а по осі абсцис – час. Оскільки під час рівнозмінного руху прискорення не змінюється, то графік прискорення є прямою, паралельною до осі часу. На рис. 1 показано графік прискорення прямолінійного рівноприскореного руху І (а = 2 м/с2) і рівносповільненого II (а = 4 м/с2).
Рис. 1
Із формули прискорення легко визначити миттєву швидкість прямолінійного рівноприскореного руху:
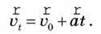
Швидкість рівнозмінного руху є лінійною функцією часу, значення проекції вектора швидкості на вісь Ox:
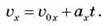
Характерні графіки швидкості рівнозмінного руху матеріальної точки для різних випадків показано на рис. 2, на якому:
– а – графік швидкості рівноприскореного руху без початкової швидкості;
– б – графік швидкості рівноприскореного руху з початковою швидкістю;
– в – графік швидкості рівносповільненого руху.
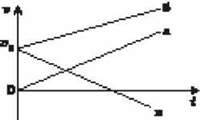
Рис. 2
В усіх випадках графіки швидкості прямолінійного рівнозмінного руху мають вигляд прямих ліній, проведених під кутом до осі часу.
Слід мати на увазі, що напрям однієї з осей системи відліку збігається з напрямом вектора початкової швидкості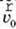 
. Якщо вектор прискорення 
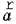спрямовано протилежно до вектора 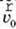, тобто a < 0, значення швидкості T у деякий момент часу може виявитися від’ємним. Це означає, що швидкість T у цей момент часу також спрямовано протилежно до напряму 0.
Середню скалярну швидкість рівнозмінного руху можна знайти як середнє арифметичне початкової 0 і кінцевої T швидкостей у цьому інтервалі часу:
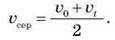
Якщо відомі час і середня скалярна швидкість, то шлях, пройдений матеріальною точкою під час рівнозмінного руху:
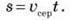
Після підстановки одержуємо:
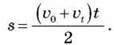
Підставляючи замість T його значення із формули і перетворюючи праву частину рівності, знаходимо вираз шуканого шляху прямолінійного рівнозмінного (рівноприскореного) руху:
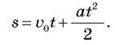
Це рівняння можна одержати в інший спосіб на підставі графіка швидкості рівноприскореного руху з початковою швидкістю (рис. 3). На цьому графіку пройдений шлях чисельно дорівнює площі трапеції, яку можна подати як суму площ прямокутника і трикутника, які. Таким чином, числове значення шляху рівноприскореного руху:
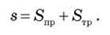
Рис. 3
Площа прямокутника дорівнює добутку основи t на висоту 0:
Sтр = 0t.
Площа трикутника дорівнює половині добутку основи t на висоту T – 0:
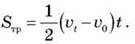
З огляду на те, що vt – v0 = at, маємо:
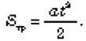
Додаючи площі S?@ і SB@, знаходять вираз для шляху рівнозмінного руху у вигляді рівняння
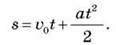
Якщо тіло рухається рівноприскорено без початкової швидкості (0 = 0), то пройдений шлях:
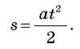
Таким чином, шлях, пройдений тілом у рівнозмінному русі, є квадратичною функцією часу і завжди додатною величиною.
Графіки шляху для різних видів прямолінійного рівнозмінного руху показано на рис. 4:
– І – рівноприскореного руху з початковою швидкістю:
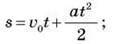
– ІІ – рівноприскореного руху без початкової швидкості:
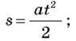
– ІІІ – рівносповільненого руху:
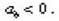
Графіки шляху І і ІІ прямолінійного рівноприскореного руху є гілками парабол, вершини яких знаходяться в початку координат. У першому випадку крива є крутішою, тобто з двох тіл, що рухаються з однаковими прискореннями (а1 = а2) раніше пройде заданий шлях те тіло, початкова швидкість якого більша. За графіком шляху рівноприскореного руху можна визначити швидкість руху точки.
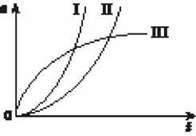
Рис. 4
Проекція переміщення під час рівноприскореного руху:
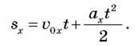
Для знаходження координати х точки в будь-який момент часу t потрібно до початкової координати х0 додати проекцію вектора переміщення на вісь Ox (рис. 5):
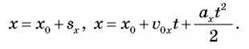
Цей вираз називають рівнянням рівнозмінного прямолінійного руху (кінематичний закон цього руху).
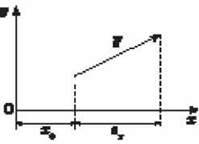
Рис. 5
Можливі залежності координати від часу у разі рівнозмінного руху зображено на рис. 6.
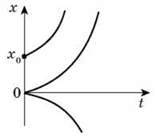
Рис. 6
Після деяких перетворень дістають рівняння прямолінійного рівнозмінного руху такого вигляду:
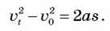
Якщо прямолінійний рівноприскорений рух тіла починається зі стану спокою (0 = 0), то рівняння набуває вигляду:
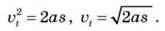
Ці формули часто використовують для розв’язування задач.
III. Розв’язування задач, складання конспекту
До конспекту учня
– Миттєвою швидкістю називається швидкість тіла в певний момент часу (або в певній точці траєкторії).
– Прискоренням тіла а називається відношення зміни швидкості тіла до інтервалу часу, за який ця зміна відбулася:
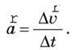
– Прямолінійним рівноприскореним рухом називається рух тіла вздовж прямої зі сталим прискоренням. Під час прямолінійного рівномірного руху швидкість тіла за будь-які рівні інтервали часу змінюється на ту саму величину.
– Швидкість: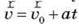 
.
– Проекція швидкості: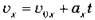 
.
– Проекція переміщення для руху без початкової швидкості:
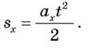
– Проекція переміщення для руху з початковою швидкістю:
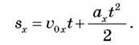
– Залежність координати від часу для руху з початковою швидкістю:
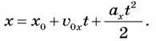
– Середня швидкість:
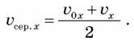
– Співвідношення між переміщенням і швидкістю:
– без початкової швидкості:
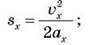
– з початковою швидкістю:
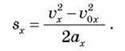
Запитання для самоперевірки
1. Що таке прискорення і для чого його потрібно знати?
2. Що таке рівноприскорений рух?
3. Як напрямлений вектор прискорення у разі прямолінійного руху?
Коментоване розв’язування задачі на дошці
Під час прямолінійного рівноприскореного руху за 10 с швидкість тіла зменшилася з 20 м/с до 10 м/с. Яким є переміщення тіла за цей час? Якою була швидкість через 5 с після початку спостереження?
IV. Домашнє завдання
1. Вивчити відповідний параграф підручника, конспект уроку, формули.
2. Розв’язати задачі.
– За першу секунду рівноприскореного руху без початкової швидкості тіло пройшло 5 м. Яку відстань воно пройшло за перші 3 с? за перші 10 с?
– Поїзд рухається рівномірно і прямолінійно зі швидкістю 50 км/год. Накреслити графік швидкості і показати на ньому модуль переміщення за 3 год. руху.
(1 votes, average: 5.00 out of 5)
Loading...